【中学受験】応用問題の解き方・解くコツ 応用問題の正体とその対策法
受験の世界にはいろんなお化けがおります。
古くはゲゲゲの鬼太郎、最近では妖怪ウォッチで沢山のお化けが出てきますが、受験界もそれに負けず劣らず魑魅魍魎がうごめくワンダーランドとなっております。
そのうちの1匹が「応用問題」です。「発展問題」などとも呼ばれていたりします。
正体は謎。解こうと頑張っても解けない。仕方なく解答を見ると、なんとなく分かったような気になる。ところが、正体も分からないし、解答を導くロジックも明らかではないので、別の応用問題に取り掛かってもやはり解けない。
そのうち、応用問題が心底恐ろしくなってきます。
取り掛かる前から「難しいんだろうなぁ〜」なんて考えておりますので、最初から腰が引け気味となります。「応用問題」と聞くだけで下半身が寒くなる、というわけです。
かくして応用問題が解けない子供、いっちょあがり!ってなわけで泣く子も黙る中学受験金型で成型された子供が量産されていくわけですね。
かくいう私も数十年前はそういう子供でありました。
ここでは応用問題の正体を私なりに明らかにいたしまして、その正体をもとに解決策と日々の学習における対策方法を書いていきたいと思います。
そんなこんなで解くコツとか解き方が何となく分かっていただけると嬉しいです。
応用問題の正体
まずは心を落ち着けましょう
「応用問題が解けなくて〜」とビクビクする前に、まずは冷静になりましょう。
目をつぶってリラックスしましょう。
はい、いいですか。
ズバリ言いますと、ビクビクするのは応用問題の正体と攻略法が分からないからです。
お化けだって正体が分かれば怖さは半減いたします。正体が分からないから「お化け」なんです。
「お化け」は目の前にいるんじゃなくて、自分の心が作り出した物体です。
冷静にお化けを分析してみて、正体が分かってしまえばまずは怖さはなくなります。応用問題しかり。
応用問題を絵にしてみる
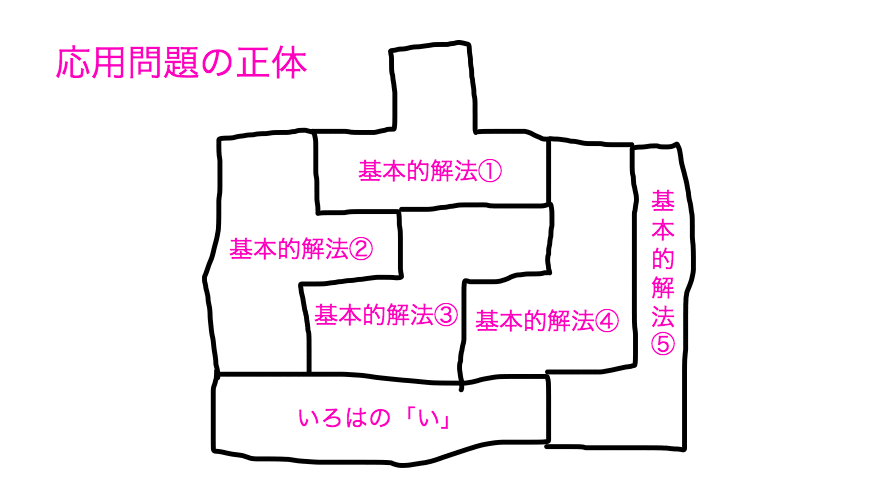
応用問題を絵にしました。応用問題は↓のような形をしています。
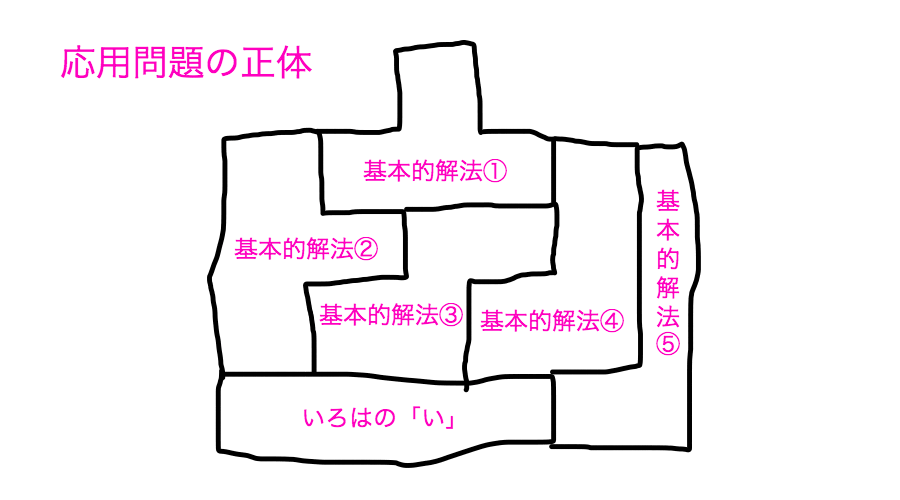
応用問題の形を絵にしたのは私が日本初ではないでしょうか。
絵が下手な上に応用問題の形を絵にするなんて頭がおかしいと思われるのは必至です。大変な勇気が必要でした。
ただ、それでも言っておきたい。応用問題はこんな形をしています。
そして応用問題をちゃんと解けるってことはこのパズルを解体できるってことです。
では特徴をあげていきましょう。
応用問題の特徴① 基本的解法の組み合わせである
絵を見ていただければわかる通り応用問題は基本的解法が組み合わさっています。
解答を見て、「なーんだそういうことかぁ」と何となく納得してしまうのは、一つ一つの基本事項の解き方は難しくないからです。
応用問題の特徴② 順を追わないと解体できない
上の絵の基本的解法③をいきなり外せますか?
いいえ、外せません。なんでかというと周りをがっちり囲われているからです。
上方向から外そうとすると、まず目につくのは基本的解法①です。ご丁寧に突起までついています。
ですからまずはひょいと基本的解法①を使って取り除きます。
次に基本的解法②の部分が外せそうですね。
次に③、④、⑤と外していくと最後にいろはの「い」が残る、と。
順を追ったら解けますし、基本的解法を知っていたら解けるということです。
大人になって人に勉強を教えることになってから、冷静に応用問題と向き合った結果、イメージとして頭に浮かんだ形を絵にいたしました。
実際、応用問題を解く時にはこういうイメージを頭に浮かべつつ解いていっております。
応用問題の特徴③ 初めにどこから手をつけるかが肝心
応用問題が解けない子や、応用問題を解けないうちというのはどこから手をつければ解けるのかが分かりません。
ですから、基本的解法①の部分から解体すればいいのに、いきなり基本的解法④を使おうと考えたりします。ところが、それじゃ解けない。当てずっぽうで基本的解法②の部分を引っこ抜こうとしますが基本的解法①の部分を外していないので、これも解けない。
いいですか。
応用問題をスイスイ解ける子ってのは例外なく、初めに基本的解法①を使う問題だなとパッと気づきます。
最初に気づくかどうか、これにほぼ全てがかかってきてしまいます。
例えば、応用問題が苦手な子だったとしても、「まずはこの問題、場合の数の解法を使ってここから解くんだよ〜」とかアドバイスしてあげると最後まで解いちゃうことがあります。
初めにどんな解法を使って解くのかに気づけば解けちゃう。逆に気づかないと一生解けない。
応用問題の特徴④ 基本的解法を知らないと解けない
上の絵を見ていただいてわかる通り、基本的解法が組み合わさっていますので、そもそも基本問題が解けないと応用問題は解けません。
これ、よくあることかもしれません。
応用問題の練習ばっかりしていて、いざ基本問題を解かせてみたら解けないなんてことはよくあることですよ。
いいですか。応用問題は基本問題(基本的解法で解ける問題)の組み合わせですから、基本問題が解けないんじゃあ解けるわけがありません。
応用問題の特徴⑤ 最後に残ったいろはの「い」
さあ、順を追って解いていくと最後に残った、いろはの「い」。ここでつまづいたらジ・エンドです。
いろはの「い」とは問題文の指示のことです。
当たり前ですが、問題文の指示に従って答えを書かないといけません。
いろはの「い」が抜けていると、
「5字から10字で記述せよ」と問題文に指示があるのに、12字書いてしまうとか。
「面積を求めよ」と問題文に指示があるのに、単位を書き間違えたり、そもそも単位を書かなかったりとか。
ということが起きます。
こういう基本的なお約束を間違えてしまうといくら能力があってもバツです。笑っていられるのは余裕があるからですよ。
試験会場で緊張して平常心を欠いていると平気でこういう間違いをやっちゃいます。
応用問題の解き方と解くコツ
さて、応用問題を解くときに大事なことをまとめておきましょう。
①一つ一つの要素は基本問題(基本的解法により解ける)
②初めにどの基本的解法を使うか
③順を追ってを基本的解法を使い解いていく
応用問題の正体が分かると上のようなことが大事だというのが分かります。
あー、これ、よく塾で言われてますよね。
応用問題を解くには基礎が大事、って。
なぜ基礎が大事なのかは分かりましたよね。
だって、基本的知識(解法)が頭に入ってないとそもそも基本的知識(解法)の組み合わせなんて解けませんもの。
じゃあ、基礎を勉強しましょう!
って、皆さん塾の先生からそんなことが聞きたいわけじゃないですよね。
基礎問題はできてるけど、それでも解けねぇーんだよッ!ってとこでしょう?
そういうあなたに耳寄りな話があります。
しかも2つも。
では行きますよ。
ひとーつ!基礎知識の組み合わせには覚えるべきパターンがあるッ!
ふたーつ!問題文で与えられた条件を整理ッ!そして隠された条件を発見せよッ!
①組み合わせパターン
まず一つ目。基本的解法の組み合わせパターンを覚えちゃうってことです。
実は基本的解法の組み合わせというのはその場で発想しなくていいものもあります。すなわち塾で教えてくれるやつです。
例を挙げます。
算数でパッと思いつくのは、つるかめ算と図形の組み合わせ、旅人算と相似の組み合わせ、場合の数と規則性の組み合わせなどですかね。
こういうのは有名でよく出てくるので、塾で組み合わせパターンの解説もしてくれますし、問題演習もやってくれます。問題はこういった組み合わせを数多く知っていることがどれだけ大事なのかをお子さんが理解していないことです。
この組み合わせを知っておくと、応用問題であっても一瞬で解き方が頭に浮かぶことがあります。解き方を知っているから、基本問題を解くのとあんまり変わらないんですよ。
時間の短縮にもなります。
②問題文の条件整理、隠れた条件の発見
パッと解法が思いつかないようでしたら、次にやるのは条件整理と隠れた条件の発見です。
まずは条件整理。問題文に書かれていることを整理していきます。
次に分かっている条件から求められることをとりあえず求めていくこと。これが隠れた条件を発見する作業です。
最後に整理した条件と隠れた条件をもとに何が分かれば(問題の急所、と呼んでおきます)知っている解き方のパターンに当てはめられるかを考えます。
で、「問題の急所」を求めるために知っているパターンを洗いざらい検討します。
なに?知っているパターンの中にない?じゃあその問題、諦めましょう!知らないことを試験の緊張感と限られた時間の中で新たに発想するってのは無理があります。
知っているパターンで使えそうなのがあったって?じゃあ全力で解くのみです。
応用問題を解くための対策法・学習法
応用問題対策
まずは基本的解法を頭に叩き込むことですね。暗記です、暗記。
次に組み合わせパターンを頭に叩き込むことですね。暗記です、暗記。
で、あとは条件を整理したり、隠れた条件を発見して、それらの条件を検討して問題の急所を特定する練習をすることです。
言うは易し行うは難し、ですね。じゃあ具体的な方法いきますよ。
①応用問題を解く 基本的解法の学習
基本的解法は塾で購入するテキストに全部書いてあります。とくに小学5年生のテキストがいいでしょう。小学5年生の1年間で基礎は全部やってくれます。テキストにも書いてあります。
あやふやなことがあれば、解き方を片っ端から暗記していきましょう。
②応用問題を解く 組み合わせパターンの学習
これは塾のテキストには解説していないものもあります。ただ、授業ではやっていると思います。
なに、書き漏らしている?
だったら参考書を買いに行きましょう。
私がイメージするのと一番近いのは算数ですと↓これですかね。
有名すぎるので今さら紹介するのもアレですが、市販されている参考書の中では一番私のイメージに近いです。私の行ったでかい本屋で見る限りでは現時点で最強の算数参考書じゃないかと思います。私が教えるよりも数段優れていると思います。
国語は残念ながらございませんでした。私の行った本屋が良くないのかもしれませんので良い参考書があれば是非教えていただきたいです。
その代わり、国語についてはあれこれ書いてます。
論説文の読み方
物語文の読み方
解くための基本的技術
いちいちリンク貼り付けるのが面倒なのでどなたか良い参考書を教えて頂けると手間が省けて最高です。
③応用問題を解く 条件整理と隠れた条件の発見の学習
条件の整理と隠れた条件の発見により問題の急所を特定するのは参考書で学ぶことではありません。
基本的解法、組み合わせパターンを学習し終えたあとで、条件を意識しながら応用問題、発展問題を解くことで身につきます。これはもう訓練によって解決して頂きたいです。
具体的な応用問題を一つ
では以下の応用問題を解いていきましょう。
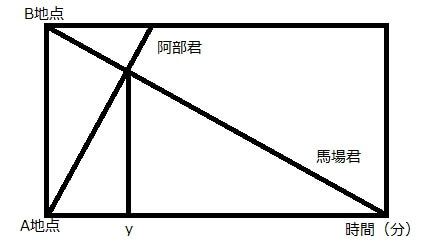
A地点とB地点の間に一本道があります。阿部君はこの道をA地点からB地点へ向かって分速50mで進みます。馬場君もこの道をB地点からA地点へ向かって一定の速さで進みます。二人は同時に出発し、B地点から250m離れた時点ですれ違いました。また、阿部君がB地点に着いてから46分12秒後に、馬場君はA地点に着きました。右の図(ここでは下の図)は、二人が出発してからの時間とA地点からの道のりの関係を表しています。二人が出発してからすれ違うまでにかかった時間をy分とするとき、yの値を求めなさい。
引用元:平成29年度 開成中学 算数 大問3(2)より
この条件を整理、隠れた条件を求めると以下のように図に書き込むことができます。
これが条件整理と隠れた条件の発見。
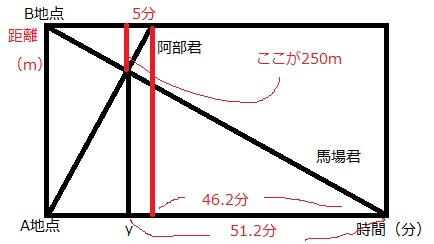
上の赤いのが書き足したところです。
上の問題は阿部君と馬場君が出会った地点がB地点から250mで、阿部君が出会った地点からB地点までたどり着くのに5分かかったという条件から、出会った地点からB地点まで5分かかったと求めています。(=隠れた条件の発見)
また、46分12秒後を46.2分に変換します。これは時間の理解を踏まえた上での数値の変換、という基本的解法を使ってます。(=条件を計算しやすい形に変換)
そしてここから相似の図形を発見し、相似比を求めます。
相似比は「y:51.2分=5分:y」
比の内項の積は外項の積と等しくなりますので、
「y×y=5×51.2」
よって「y×y=256」
となります。
上の条件を満たすyは16ですので、答えは16分。
この問題を解くには、
▼条件を求める段階
①速度の問題を解くのに必要な基礎知識
②時間の理解を踏まえたうえでの数値の変換
▼解答を導く段階
①ダイヤグラムに変換する(幸いなことにこの問題ではダイヤグラムは与えられていました)
②相似の図形を発見する
③相似比を求める
④比の性質を使う(内項の積と外項の積は等しくなる、という性質)
という段階を経る必要があります。6個もの基本的解法を知っていて、それを使わないと解けない問題なんですね。しかも旅人算の問題のようでいて、最終的には比でないと解けないというおまけつきです。
旅人算だけ知っている子供じゃ絶対解けねぇ〜。
ただ、よく見て欲しい点があります。ちゃんと基本的解法さえ身についていれば簡単に解けちゃう点です。
開成中学ってこういう問題多いです。
なんとなく応用問題の解き方は分かりましたでしょうか?
てなわけで小学6年生の冬前には一通りの応用問題を解けるようにしちゃって、1月はハワイにでも行っちゃったらいいじゃん!正月特訓なんて意味ない特訓、スルーしちゃってさ!
バーイ。
あわせて読みたい
最新のホカホカ記事
最新のホカホカ記事の一覧はこちらから書いている人の紹介
星一徹のプロフィールはこちらから- 前の記事

開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問4(5)図形ー第8回 2018.06.19
- 次の記事

開成中学入試問題「算数」を徹底解説、平成28年度大問1(1)①比の問題ー第9回 2018.06.27