【中学受験】場合の数　ならべ方（順列）と組み合わせの違い・公式の意味・問題演習

予習シリーズ5年上巻　第11回「場合の数　ならべ方」と第12回の「場合の数　組み合わせ方」は二つで一つの単元でございます。

高校数学ではならべ方を「順列」、組み合わせは「組み合わせ」なんて呼んで学習いたします。

まとめて、場合の数と言ったりします。

場合の数は数学Aで習う内容でして、高校1年生の学習内容でございます。

ちなみに、学校にもよりますが高校卒業に数Aは必修ではありません。数1のみ必修です。

高校まで進学した親御様は、場合の数でP（permutation）とかC（combination）とか使って計算したのを覚えておられるかと思います。

まさにアレです。

アレを小学校5年生でやっちゃおうってわけですよ。

正確に言いますと小学4年生ですね。

小学4年生では公式を使わずに樹形図等で解くやり方を習います。

小学5年生ではいよいよ公式を使って解いてまいります。

はるか遠い昔の記憶を呼び覚ましてください。

PとかCとか使って計算するときに一番困ったのはなんですか？

公式？計算？

違いますよね。

どんな場合にPを使って、どんな場合にCを使うのか分からなくなりませんでしたか？

実際のところPだのCだのの公式は覚えればすぐに使えます。

が、問題が「ならべ方＝順列＝P」を問うているのか、「組み合わせ＝C」を問うているのか判別できなくなるのが厄介なんです。

なぜ判別できないのかというと公式だけ覚えるからです。

ですから何のために使うものなのか、どんな場面で使うのか、なぜそういう公式で求められるのかを知っておいたほうがいいわけですよ。

とりあえずはならべ方（順列）、組み合わせの公式をご紹介しつつ、どんな問題で使うのか、なぜその公式で求められるのかをお話ししてまいります。

ならべ方（順列）と組み合わせの公式

さて、まずは公式と、どうしてその公式で求められるのかをやっていきましょう。

ならべ方（順列）の公式

n個の中からr個取り出して並べるとき、

順列の数＝n×(nー1）×（n−２）×（nー３）・・・×（nーr＋1）

で求められます。

これが公式です。

高校数学では↓こんなふうに表したのを覚えていらっしゃいますかね？

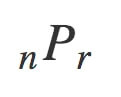
たとえばA、B、C、D、Eくんの中から委員長と副委員長を一人ずつ選ぶとします。

そのときのならべ方（順列）は、

5×(5ー1）＝20

となります。

これを高校数学では↓このように表しましたよね。

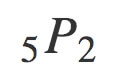
ちょっとずつ記憶がよみがえってきましたか？

いいですね。

なぜこのように求められるかというと、たとえば委員長をAくんとするじゃないですか。

すると、副委員長はBくんかCくんかDくんかEくんの4人から選べます。

つまり、委員長を誰かに決めると副委員長は4通りの選び方があります。

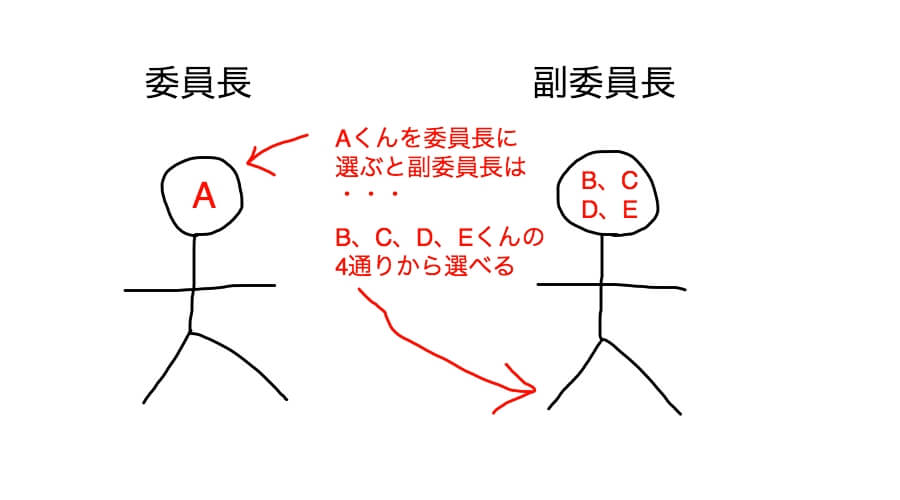
ところで委員長を今はAくんとしましたが、BくんでもCくんでもDくんでもEくんでもいいわけです。

つまり委員長の選び方は5通りありますよね。

ですから、

5（委員長）×4（副委員長）＝20

で20通りとなります。

これがならべ方（順列）の公式と基本的な考え方です。

組み合わせの公式

n個の中からr個を取り出すのが組み合わせです。

ならべ方（順列）と違って並べません。

ただ取り出すだけです。

組み合わせの公式は↓のように表せます。

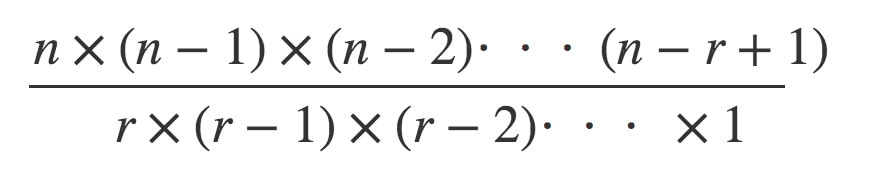
高校数学では↓のように表していましたよね。

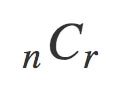
↓こんな問題が「組み合わせ」の問題です。

A、B、C、D、Eくんの中から委員を二人選ぶとすると何通りありますか？

ならべ方（順列）は委員長と副委員長でしたね。組み合わせでは委員です。

組み合わせでは取り出した要素を区別しません。

少し例をあげましょう。

・10人の中から2人の委員を選ぶのは「組み合わせ」です。

・10人の中から旅行委員と保健委員を一人ずつ選ぶのは「ならべ方（順列）」です。

・10個の赤いボールと5個の青いボールから3個のボールを取り出すのは「組み合わせ」です。

・10個の赤いボールと5個の青いボールから3個のボールを取り出して一列に並べるのは「ならべ方（順列）」です。

・10件の居酒屋から今日行く店を3店選ぶのは「組み合わせ」です。

・10件の居酒屋から3店選んでそれぞれ18時、20時、22時に予約をとるのは「ならべ方（順列）」です。

なんかイメージつきました？

「組み合わせ」は取り出すだけです。

「ならべ方（順列）」は取り出した要素を区別します。

A、B、C、D、Eくんの中から委員を二人選ぶ問題を例にとって説明しましょう。

「組み合わせ」ではA、B、C、D、Eくんの中から二人選ぶだけです。

なので、A、Bくんの二人を選んだとすると、それで1通りです。

「ならべ方（順列）」ですと、選んだ二人はそれぞれ委員長と副委員長に任命されます。

なので、「Aくんが委員長、Bくんが副委員長」の場合と「Aくんが副委員長、Bくんが委員長」の場合は異なります。

ですから2通りです。

「組み合わせ」と「ならべ方（順列）」は似ているようで全然違いますよね？

全然違うにもかかわらず似ています。

「組み合わせ」と「ならべ方（順列）」は阿佐ヶ谷姉妹みたいなものです。

よく似てますが血がつながっていません。

全くの別物です。

すなわち、場合の数では「ならべ方（順列）」なのか、「組み合わせ」なのか判別するのがめちゃくちゃ大事です。

さて、A、B、C、D、Eくんの中から委員を二人選ぶ場合の数を求めましょう。

これは↓のようにして求められます。公式をあてはめるだけですね。

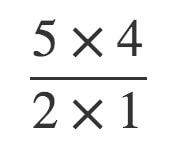
答えは10通りです。

高校数学では↓のように表していたかと思います。

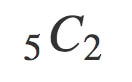
完璧に思い出していただけましたかね。

四半世紀前に習ったPとかCとかのややこしい話です。

では「組み合わせ」の式の意味を説明していきます。

↓こうです。

上の式（分子）はならべ方（順列）の場合の数を求めています。

下の式（分母）はならべ方（順列）のダブリを除いています。

これで組み合わせの場合の数が求められるのですが、分母の「2×1」って一体なんスかね？

ならべ方（順列）ではA・BとB・Aは違うものとして扱っていたじゃないですか。

Aが委員長、Bが副委員長。

Aが副委員長、Bが委員長。

違いますよね。

組み合わせはA・BとB・Aは同じものとして扱うんですよ。

Aが委員、Bが委員。

Bが委員、Aが委員。

どっちも同じですよね？

なので、ならべ方（順列）と同じように場合の数を求めるとダブリが発生するんです。

分母でやってるのはダブリの排除です。

この場合は5人から2人選ぶ場合のダブリを排除しました。

では、5人から3人選ぶ場合のダブリはどうなりますでしょうか？

A、B、Cくんを取り出す場合を考えてみますよ。

すると、ならべ方（順列）は↓の6パターンあります。

A・B・C、A・C・B、B・A・C、B・C・A、C・A・B、C・B・A

ところが、組み合わせですと上の6パターンはすべて同じと見なされて、1パターンと数えられます。

ですから、6で割る必要があるんですよ。

つまり、5人の中から3人選ぶ組み合わせを式で表すと↓のようになります。

1 2 3 次へ >

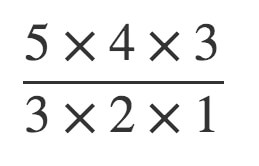
あわせて読みたい

最新のホカホカ記事

書いている人の紹介