【中学受験】算数　円の転がり移動・作図の方法

「おいおいおい、三角形のまわりをミミズがのたくっているが一体これはどういうことなんだ？」

おやおや、お子さんが予習シリーズに奇妙な線を書いているみたいですね。

何やら事件現場に引かれたチョークのようにも見えますね。

さて、新版予習シリーズ算数5年生上巻9回の円の転がり移動の話でございます。

この回のキモは作図です。

正確に作図ができるかどうかが転がり移動のキモです。

「作図なんてできるっしょ、フリーハンドで！」

いえいえ、そこは小学生。

フリーハンドで作図をするとヨレヨレの線になってしまい、作図前よりも混沌とした図形があらわれるのは必定。

ってか、私からしますとなんでフリーハンドで書くのかがよく分かりません。

定規とコンパスを使いましょう。

「いや、でも本番の入試ではフリーハンドで書けた方がいいし・・・」

まあまあ、たしかにそうです。

ですが本番の入試でも定規やコンパスは持ち込み可能な学校は多いです。

（※注　各学校の募集要項で持ち込み可能なものをよくご確認ください。）

確かにテストではフリーハンドで正確に書けたほうが速いかもしれません。

が、練習段階ではヨレヨレの線を書くよりも定規とコンパスを使ってちゃんと作図したほうがいいです。

練習です。練習。

実は絵や図形をきれいに書ける人は手が器用というより、目がいいらしいですよ。

道具を使って作図することで正確な図形や絵を目で覚える。するとフリーハンドもうまくなります。

割と常識なんですが知らない人も多いのであえて言っときました。

さて、では新版予習シリーズ算数5年生上巻9回の円の転がり移動をやっていきます。

まずは多角形の周りを円が転がる様子、そして円やおうぎ形の周りを円が転がる様子を作図の仕方とともにお話ししてまいります。

シュワッチ。

円の転がり移動　多角形の周りを転がる

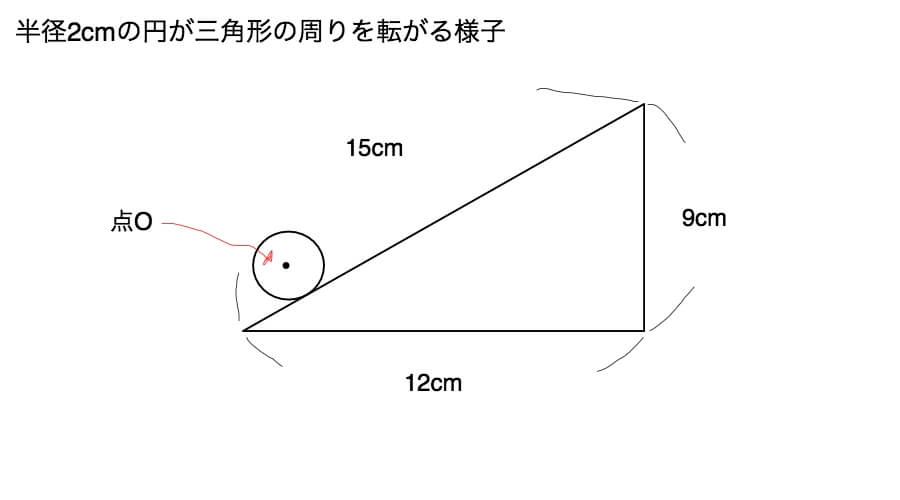
こんな図形を題材にお話をしてまいります。サイズ感がおかしいとかいうクレームは一切受け付けませんよ。

円の転がり移動の作図の基本からいきます。

円の転がり移動　作図の基本その１　平行な線を引く

直線と平行な線を引くのが超基本中の基本です。

立体図形を描く時の基本でもあります。

では三角定規を用意してください。

三角定規を使って平行な線を引く時はこのようにします。

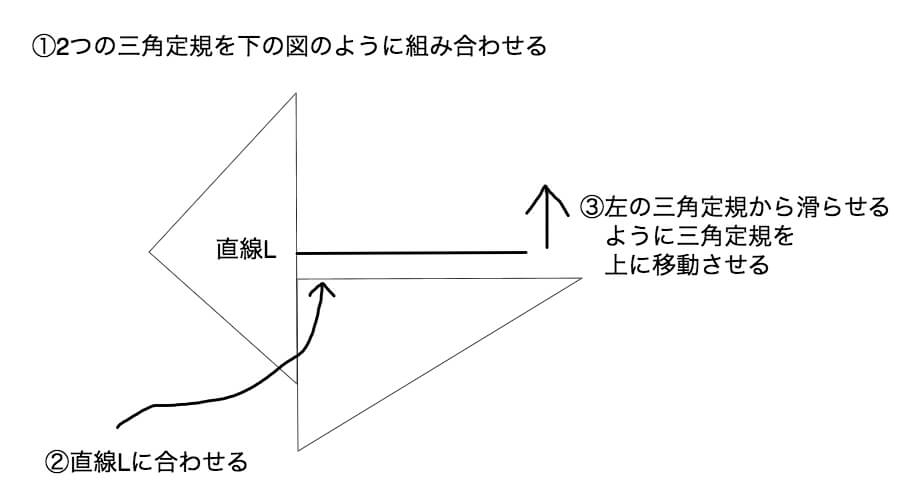
このようにすると三角定規を使ってきれいに直線と平行な線を引けます。

では円の転がり移動の作図の問題に戻りましょう。

点Oの直線における動きを作図します。

上で説明した三角定規を使って平行な線を引くやり方を必ず使ってくださいね。

するとこうなります。

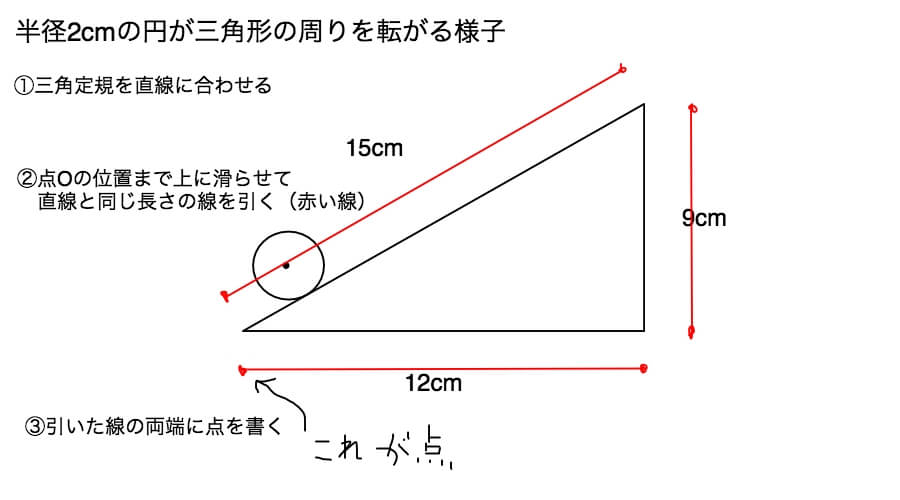
こんな感じに引けましたか？

三角定規を使って平行な線を引くのは小学校の算数で習います。

真面目に学校に行ってればできるはずです。

もし5年生のお子さんが三角定規を使って平行な線を引けないのだとしたら学校の授業を聞いてない証拠です。

で、平行な線を引いたら両端に点を書くのがポイントです。

弧と直線との境目がはっきり分かるからです。

点を書いておかないとどこまでが直線で、どこからが弧なのかわからなくなります。

あと、コンパスで弧を描くときの目印にもなります。

ちょっとした工夫でめちゃくちゃわかりやすくなりますのでぜひやってください。

円の転がり移動　作図の基本その2　コンパスで弧を描く

では次に弧を描きます。

このときに使うのはコンパスです。

さすがにコンパスの使い方は分かりますよね。

コンパスの針を三角形の頂点にぶっ刺して、鉛筆の先を点に合わせます。

あ、ちなみにコンパスは色々な種類が売ってますが、シャープペンシル型のコンパスがオススメです。

きれいな弧を引けます。

するとこうなります。

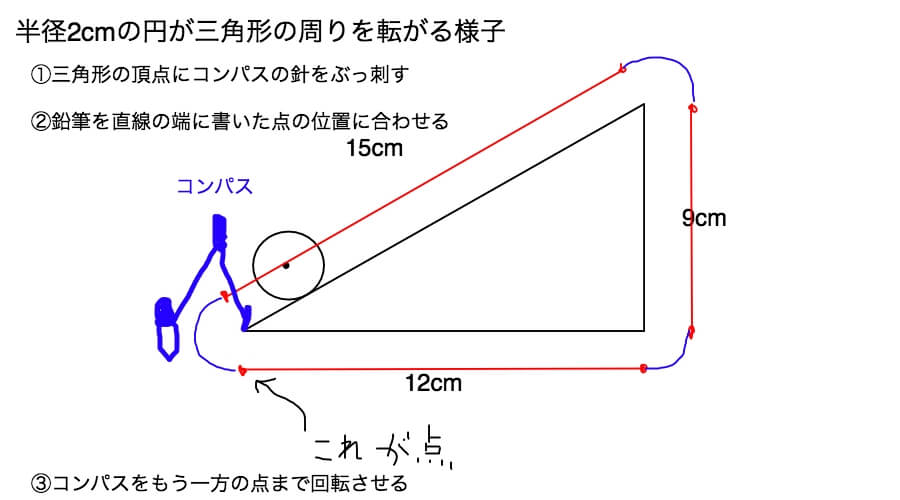
コンパスで描いた弧は青色の線です。

若干、ヨレているのは私が画像ソフトをつかってフリーハンドで描いたからです。

無料の画像ソフトなので弧を描けませんでした。

コンパスの絵も少しおかしいのはご容赦ください。

三角形の頂点は3つありますので、弧は3つ描けます。

すると上のような感じになります。

次に、三角形の頂点の位置から平行に引いた直線まで垂直な線を引きます。

このときもフリーハンドではなく三角定規を使いましょう。

円の転がり移動　作図の基本その3　頂点から垂直な線を引く

頂点の位置に三角定規の直角部分をあてます。

そしてグイッと平行な直線まで垂直な線を引きましょう。

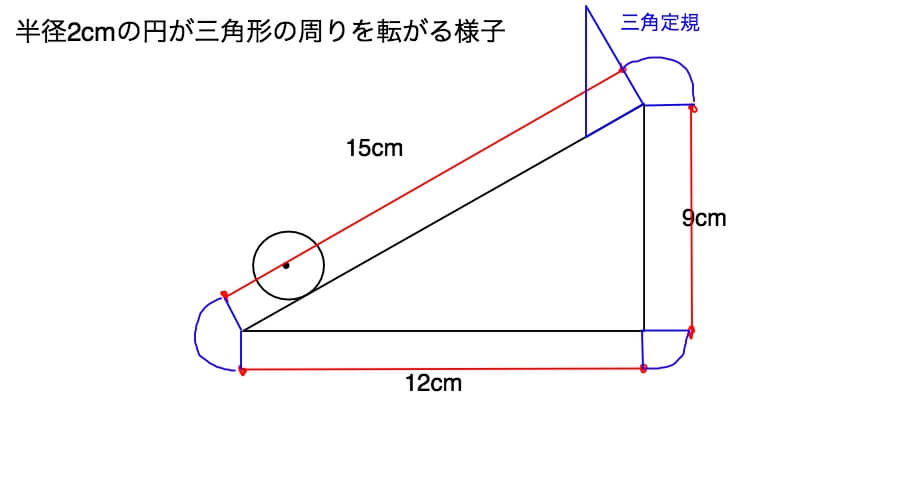
やたらと小さい三角定規ですが、まあいいでしょう。

三角定規の直角部分を使うと、三角形の辺と垂直な直線がきれいに引けます。

では最終段階です。

ダルマに目を入れていきましょう。

円の転がり移動　作図の基本その4　長さと角度を書き込む

ここまで描いてきた図形にいよいよ長さと角度を書き込むときがやってまいりました。

と、ここまでで大変なことに気づいてしまいました。

私、三角形の角度を記入するのを忘れていました。

もう、面倒くさいので上の画像は訂正しません。

ここで三角形の角度を入れちゃいます。

なお、辺の長さの比が3：4：5の三角形の直角以外の角度は、厳密には小数点以下無限に続きます。

無限なんか計算しようがないので、ここでは角度の数値は丸めてます。

では書き込んでいきます。

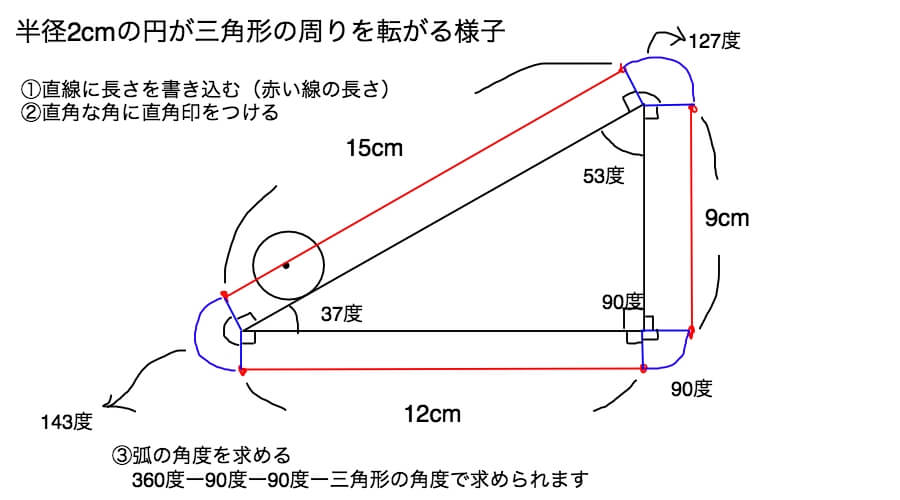
最初に赤い線に長さを書き込みます。

三角形の辺と等しいのですぐに書き込めますね。

次に直角な角に直角印をつけます。

ひとまず直角印を書き込むのは古代エジプトから続く人類の常識です。

最後に弧の角度を求めていきます。

360度から直角2つと三角形の角度を引くと求められます。

360ー90ー90ー37＝143度

という具合です。

仕上げにこんな問題を解いてみましょう。

円の転がり移動　点Oが動いた線の長さを求める

点Oが動いた線の長さは直線（赤色）と弧（青色）の長さを求めて足せば出ますよね。

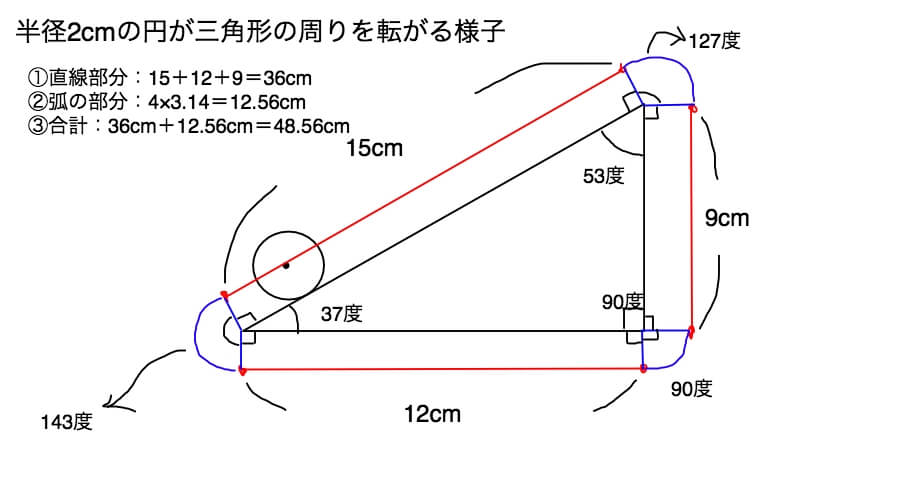
直線部分は15cm、12cm、9cmですから足して36cmです。

弧の部分は143度と127度と90度です。

1個ずつ求めていくのはヤバい作業になりますから、こういう時は全部の角度を足しちゃいましょう。

143＋127＋90＝360度

はい、きれいに360度と求められましたね。

ってことは円の直径×3.14で答えがでます。

つまり、

4×3.14＝12.56cm

です。

最後に直線の長さ36cmと弧の長さ12.56cmを足すと、

48.56cmと求められました。

さて、ここでほんのり豆知識です。

多角形を円が転がり移動するとき、弧の角度の合計は360度になります。

嘘だとお思いなら六角形とか七角形でやってみてください。

360度になりますから。

ただし注意点があります。

へこんだ多角形の場合は360度になりません。

こういうやつ↓

ここでゲストとして松平健さんにお出ましいただきました。

私のブログには2回目のご登場です。

スターが360度にならないと言っているので間違いありません。

では最後に円が通った後の図形の面積を求めます。

円の転がり移動　円が動いた後の図形の面積を求める

さて、おなじみのやつです。

円が動いた後の図形の面積を求めましょう。

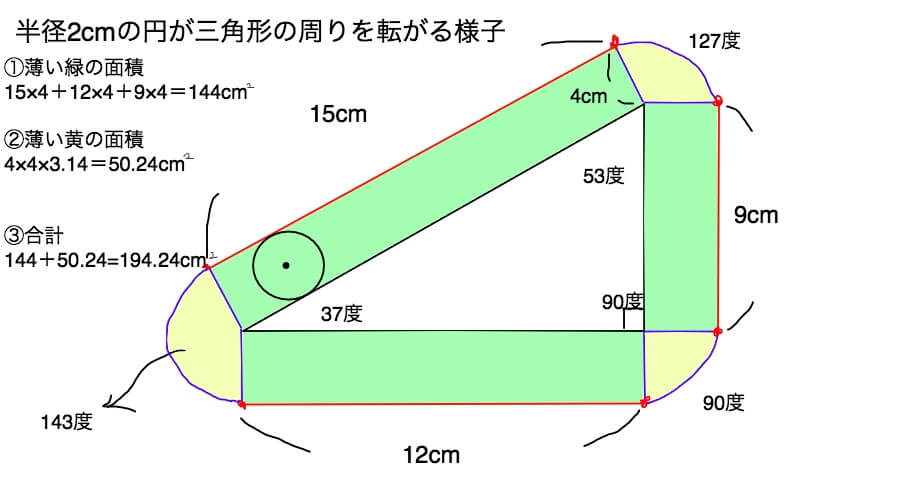
緑色の部分の面積は15×4＋12×4＋9×4で求められますね。

こんなときは計算の工夫を使っちゃいましょう。

（15＋12＋9）×4＝144　平方センチメートル

黄色の部分の面積を次に求めます。

3つの弧の合計角度は360度でしたね。

ですので、半径×半径×3.14で黄色の部分の面積が求められます。

4×4×3.14＝50.24　平方センチメートル

緑と黄色の面積を足すと、

144＋50.24＝194.24　平方センチメートル

はい、答えが出てきました。

簡単ですね。

ここでまた豆知識です。

円が移動した後の図形の面積は、

中心点の移動距離×高さ

で求められます。

いきますよ。

中心点Oの移動距離：48.56cm

高さ：4cm

48.56×4＝194.24　平方センチメートル

ね、答えが同じになったでしょう。

多分、塾で習うと思いますが、予習シリーズに書いてなかったので書いときました。

私は予習シリーズがミスって書き漏らしたわけではないと思ってます。

予習シリーズの中の人もそれくらいは知っているに決まってます。

もう一度言いますが、円の転がり移動のポイントは正しい作図です。

そして、最初は愚直に作図し、愚直に長さや面積を出していった方が身につきます。

便利なやり方は重宝しますが、毒にもなります。

あえて便利なやり方を書いてないのは基本に忠実にやれよ、という予習シリーズの中の人からのご託宣でしょう。

理屈をちゃんと理解していないお子さんには教えないほうがいい知識です。

では次におうぎ形の周りを転がる円の話にいきます。

1 2 3 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介