開成中学入試問題「算数」を徹底解説、平成28年度大問１（１）①比の問題ー第9回

落ち着いて条件を明らかにしていきましょう

開成中学校の平成２８年度入試問題「算数」大問１の（１）をやっていきたいと思います。

何度か言っていますが落ち着いてまずは条件を明らかにしていきましょう。いきなり解こうとしないことが問題を解くためのコツです。

いきなり解こうとするとドツボにはまります。

なぜドツボにはまるかというと、条件を明らかにすることと解く作業という種類の異なる作業をいっぺんに行うからです。

普通の人は種類の異なる作業をいっぺんに行うことができないと私は考えています。基本的に人間はシングルタスクです。マルチタスクのように見える人でも、少なくともある瞬間だけを切り取ればシングルタスクです。

読む、考えをまとめる、書く等、これらの種類の異なる作業を一連の作業として行っているように見えても、一瞬一瞬では一つのことしかできません。

そして効率の良い作業をするためには、種類の異なる作業をきちんと分けて集中して行うことが肝要です。

また、問題を解決するためには順番も大事です。解決するために与えられた前提条件を把握していないのに解決することはできません。

正しいインプットが正しいアウトプットを導くように、受験問題においても正しい条件の理解が正しい解につながるのです。

step1　条件を整理、発見する

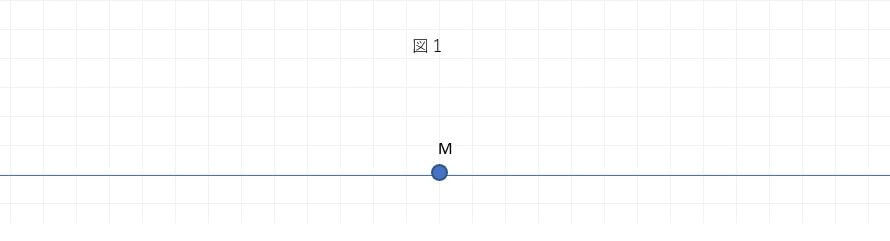
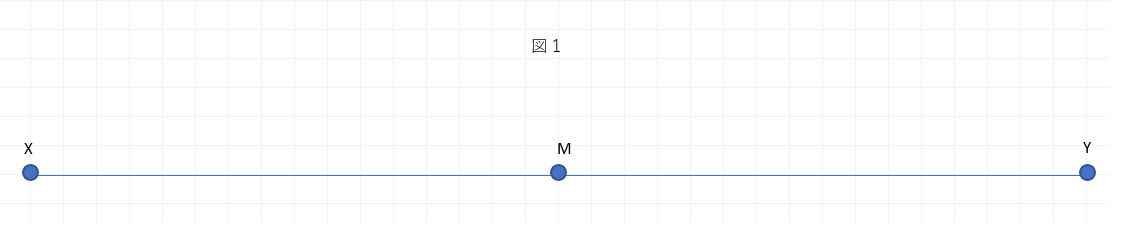
２つの地点X、Yを結ぶ道があります。A君はXからYへ向かって、B君はYからXへ向かって移動し、地図上の中間地点Mで出会うことにしました。地図には等高線が描かれていなかったため、B君は、図１のように2人とも水平な道を移動すると考えました。

 B君は、自分がA君より早く移動できること、おのおのがつねに同じ速さで移動することの２つをふまえて、A君が出発してから15分後に出発しました。これで2人はちょうどMで出会うはずでした。

ところが、実際には図２のような下り坂がありました。X％の下り坂では移動する速さがX%だけ増すことになります。ここで下り坂がX％であるとは、

X＝（下向きに移動する長さ）/（横向きに移動する長さ）×１００

のことを指します。それでも無事に、2人はちょうどMで出会いました。このとき、以下の問いに答えなさい。

なお、3辺の長さの比が３：４：５や５：１２：１３となる直角三角形を利用してもかまいません。

（１）①A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍ですか？

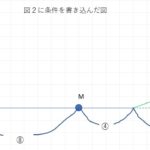
さて、この問題の条件を明らかにします。

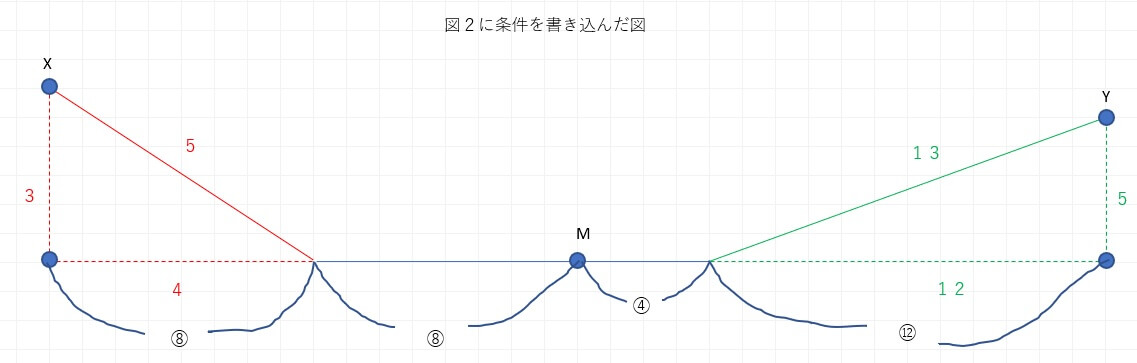
赤と緑の数字は、それぞれ赤と緑の線で表された三角形の辺の比です。

また、〇で囲われた数字は距離です。

ここから分かるのは、B君が事前に想定していた到着時間の前提が⑯という距離を辿ってM地点まで到着するということだったのですが、下り坂があって速度が増したことによって実際は変わってしまったという点です。

では、どのように変わったのかというと、

距離においては、X地点から出発したA君は⑧×5/4＝⑩という下り坂の距離と平坦な道のりの⑧という距離を進むことになりました。

速さにおいては、X地点から出発したA君は下り坂では3/4％増しの速さで進むことになりました。

時間においては、X地点から出発したA君は⑩÷7/4＋⑧＝96/7という時間で進むことになりました。

step2　解答の方向性を決める

当初の想定である⑯という距離を進む時間は、実際は96/7となってしまいました。下り坂で速さが増したのと、下り坂を進む距離が変わったからです。問われているのは当初の想定の何倍の時間がかかったかということですから、当初の想定と実際の時間を比べることで解答が求められそうです。

step3　解答の道筋を決める

⑯と96/7の比較ですから、両者の分母を揃えてあげれば比較が可能になります。

step4　数式を立てる

112/7（想定）：96/7（実際）　となります。問題文は当初の想定の何倍かということですから９６÷１１２となります。

step5　計算する

９６÷１１２で、答えは6/7倍となります。

条件さえ正しく導き出せれば自動的に解答まで至る

ここで分かるのは条件をきちんと明らかにすることで解答がほぼ自動的に導かれたということです。

問題文をもとに条件を整理して、隠れた条件を正しく見出すことが開成中学校の算数を解くうえでは最も大切だと考えています。そこができていれば解答は簡単に導き出せます。

解けない理由はただ一つで、問題文で与えられた諸条件の整理と、与えられた条件から導出される隠れた条件を見いだせていないからです。

冒頭にも申し上げたようにいきなり解こうとしないということの趣旨はここにあります。解答までの道筋は遠回りに思えてもきちんと段階を踏んで、とくに条件の整理・発見に力点を置いてやっていきましょう。

次回は同じように②も解いていきます。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介