開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問4（５）図形ー第8回

インチキをしないと解けませんでした

正直に告白をしておきましょう。この問題については方程式を使わないと解けませんでした。中学受験では、少なくとも塾では教わらない方程式を使用して解いたのでありますから、これはインチキであります。

言い訳になってしまいますが、この問題を方程式を使わずに解くのは私には無理でした。

方程式で解いた後、解答も見てみましたがさっぱり意味が分かりません。なぜそんな解き方が導き出されるのか、どうしてそんな発想が出てくるのかが分かりませんでした。詳細は市販の過去問集の解答を見てみてください。意味が分かりません。私が使った方程式による解き方の方がよっぽど分かりやすいです。

step1　条件を整理、発見する

まずは問題文を見てみましょう。

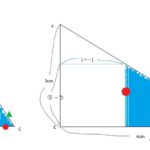
図３の状態のあと、この容器に水をさらに追加したところ、面DEFを下にして水平な床に置いたときと、面ACFDを下にして水平な床に置いたときとで、容器の下の面から水面までの高さが等しくなりました。このとき、等しい水面の高さは何ｃｍですか。

さて、この条件と前の問題までで分かったことを条件として、図形を描いてみましょう。

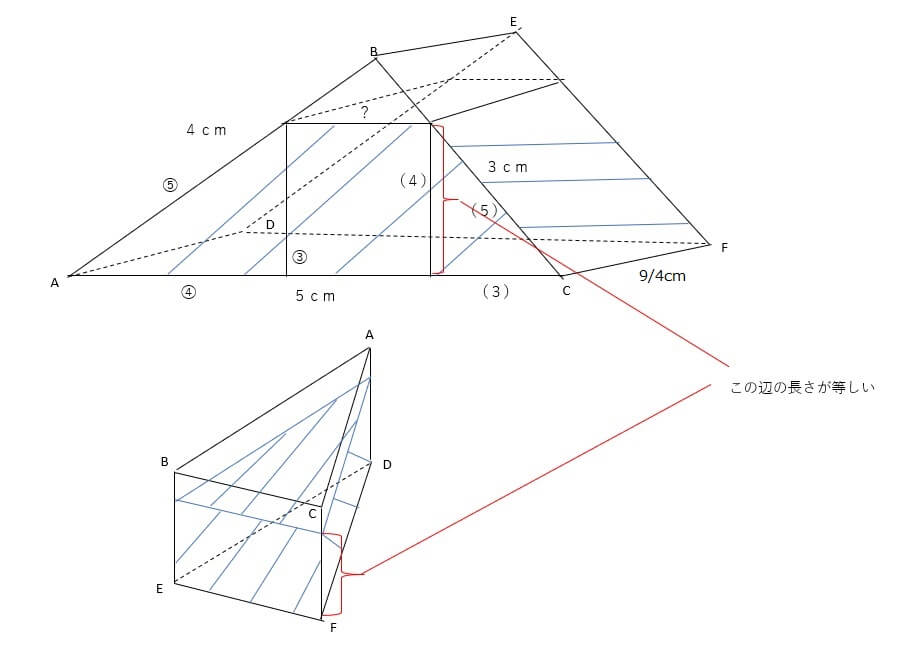
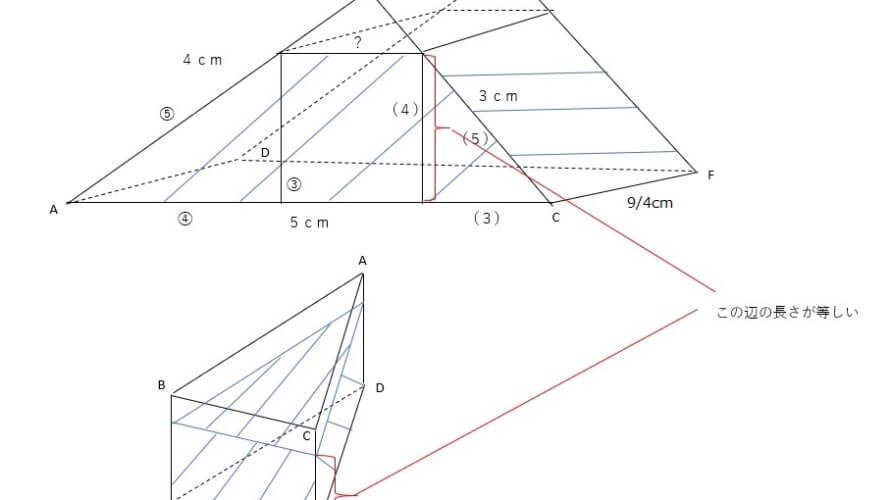
上の図の面ACFDを底面とした図形の体積と、面DEFを底面とした図形の体積が等しくなります。そして、高さが等しいそうなので「この辺の長さが等しい」と指し示している辺の長さが等しくなります。

また、上の図のCFはこの問題の（４）で解いているように9/4ｃｍとなります。

そして、上の図の側面にあたる台形の両脇にある三角形は三角形ABCと相似の関係になり、相似なので比は３：４：５となります。図形の中に書き込んでいる③：④：⑤と（３）：（４）：（５）がそれにあたります。

で、上の図の下底は５ｃｍと分かっていますが、上底は分からないので「？」と置いております。

step2　解答の方向性を決める

ここまでで方向性を決めることができます。

？の辺の長さが分かれば相似比を使用することにより解けることがわかります。台形の底面の５ｃｍから④、（３）を引いた値が？なので、５ｃｍから？を引けば④と（３）の和となるからです。（３）は、後述しますが、〇の数値に変換することが可能なので、５ｃｍから？を引いた値は〇で表すことができます。すると①の値が求められ、この問題で問われている台形の高さは③なので、①の値に３を掛ければ求めることができます。

？を求めるのには等式を利用しようと思います。面ACFDを底面とした図形の体積と面DEFを底面とした図形の体積が等しくなるのでこれを等式に表していくことで解くことができそうです。この等式には？以外の未知の数がないので？は必ず求められると考え、等式を利用することにします。

そして？の値が分かれば相似の図形の性質、すなわち相似比により解答を得ることができます。

step3　解答の道筋を決める

面ACFDを底面とした図形の体積は（AC＋？）×高さ÷２×CFとなり、

面DEFを底面とした図形の体積は三角形の面積×高さとなります。

そしてこのときの高さは等しくなります。「高さ」とでも置いておきましょう。

step2で？以外の未知の数はない、と言ったのに対して「高さ」というのも未知の数である、と思うかもしれません。ですが、「高さ」は面ACFDを底面とした図形の体積と面DEFを底面とした図形の体積で同じ値であるため等式から消去してしまうことができます。

ですから？以外の未知の数はないと言ったのです。

step4　数式を立てる

（５＋？）×「高さ」÷２×9/4＝６×「高さ」となります。

この式を変形すると、

（５＋？）×「高さ」÷２×9/4ー６×「高さ」＝０となります。

「高さ」という未知の数は両辺で同じ値なので消してしまいましょう。

（５＋？）×÷２×9/4ー６＝０

step5　計算する

両辺から６×「高さ」を引くと、左辺は上記の式となり、右辺は０となります。両辺から同じ値を引いているので等式は成立します。そして「高さ」は共通の値なので消してしまいます。そして÷２は1/2と同じなので1/2×9/4で9/8としておきます。

どんどんいきましょう。

（５＋？）×9/8－６＝０

はい、これを更に推し進めます。

（４５＋？×９）÷８－６＝０

はい、どんどん中学受験から離れていきますね！

４５＋？×９－４８＝０

もはや完全な方程式！（ちなみにここでは÷８を外すために「－」の左右に８を掛けました）

？×９－３＝０

この等式を満たす？は1/3となります。？は1/3cmで確定です。

step4　数式を立てる

？が判明しました。

ではstep2で考えた方向性（まずは等式により？の解を求め、次に相似比を利用して解く）をもとに相似の図形の性質を利用していきましょう。

③＝（４）です。〇：（）の比は４：３となります。

さて、上の図の台形の下底は次の等式が成り立ちます。

５ｃｍ＝④＋（３）＋1/3

で、（３）を〇に変換しますと、⑨/④となります。

これを上の等式に当てはめると、

14/3ｃｍ＝④＋⑨/④　となります。

step5　計算する

これを計算すると、14/3ｃｍ＝㉕/④となり、

①は14/3×④/㉕で56/75ｃｍとなります。この問題で問われている高さは③ですので、

③×56/75ｃｍで、

答えは、56/25ｃｍすなわち２と6/25ｃｍとなります。

という等式を利用して解く方法が私としては一番わかりやすいと思います。等式を利用していることから方程式のようになってしまい、これはいけないと思い、一体どうやって解くのかと過去問の解答を見たところ、どこから発想したらそんな方法が出てくるのかさっぱり分からない解き方を使っています。

いずれにせよこの問題のポイントはstep1で見えている条件を洗い出し、同時に隠れた条件（ここでは相似と相似比のことですね）を見出すことです。ここまで洗い出せるとstep2以降は楽に発想できます。

勝負のポイントは条件をいかに正確に洗い出すことができ、方向性を見定め、その後の過程を誤りなく、論理的に導くことができるかです。

最初に申し上げたように私は方程式の考え方を用いました。が、本質的には算数の問題を解く、というのは与えられた条件や隠された条件をもとにどうやって解くかを考え、設計し、そして解くということに尽きます。

計算式を立てたり、計算をする前段階で、一体どのような条件が与えられ、どのようにしたら解答を導くことができるのかという能力が中学受験の算数を解くうえでは重要になると考えています。

本当に見るべきは方程式を使うまでの段階にして如何に至ったのかという点です。よく「方程式を使えば簡単に解ける」と言われたりしますが、そんなに甘くありません。方程式は単なる手段です。方程式を使う段階まで至れるように読解能力や設計能力を鍛えなければ問題を解くことはできません。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介