【中学受験】算数が苦手な子のための奥義　問題文の条件整理　苦手を克服しよう

先日、公式とか解法とかって大事なんだぜーと書きましたら、

「そもそも条件整理ってなんですか？」

とご質問いただきましたため、さささっと算数の条件整理について話していきたいと思います。

最初から結論を言ってしまいますと、条件整理ってのは問題文を正しく読むのとほぼイコールの技法です。で、算数が苦手の子は問題文をちゃんと読んでないのであります。

そりゃ問題文をちゃんと読んでなかったら解けるわけないでしょう。

でも、問題文を読まない子なんているの？

ってわけですがいっぱいいます。まずはそんな子の特徴から話していきたいと思います。

↓は前回のお話。

【中学受験】算数の解法パターン・公式暗記の効能　おすすめ問題集の紹介も併せて

中学受験の算数が苦手な子のよくある特徴

これは私が教えていた実感なんですけどね、算数が苦手だとか苦手分野があるっていう子はそもそも問題文をちゃんと読んでないんですよ。

嘘つけ、読んでるぜ！とだいたい言うんですけど、全然読めてないことが殆どでした。そりゃ表面的には読んでるかもしれませんよ。

でもね、図にしてみて、とか、グラフ書いてみてよ、とか意地悪なことを言うマルキ・ド・サドを前にして、「えーと、うーんと」とか悩み始めるんです。大抵ね。

それ、読んでないってことっすよ。ちゃんとね。

さて、「ちゃんと」ってのがクセモノなのであります。どのくらいが「ちゃんと」で、どのくらいまでが「適当」なのか基準を示してくれる人ってあんまりいないじゃないですか。

ちゃんと掃除しろよ、って言ったって人によって「ちゃんと」の定義が異なるものであります。ダスキンのクリーンレディーだったら隅から隅までしっかり汚れをふき取ってくれますし、ボンクラ父ちゃんだと部屋の隅っこは埃だらけ、ソファも移動して掃除しないものですからソファの下は天外魔境になっていたりしますよね。

勉強もそう。

当然ながら、親御様の「ちゃんと」、先生の「ちゃんと」、子供の「ちゃんと」はぜーんぶ違うってわけです。

ですから「ちゃんと問題文を読みなさいよ！」と怒られても一体どのくらいまでが「ちゃんと」なのか分からないと子供としては途方に暮れてしまうわけです。This is 体験談。

そこで、子供のレベルに応じて「ちゃんと」の基準値を示すことが大事でありまして、私は基本的には図とかグラフとか絵とか樹形図とかその他諸々に問題文を正しく変換できるのをもって「ちゃんと」の基準値として示しておりました。

問題を正しく別の形に置き換えられるってのは「ちゃんと」読んでないとできないですからね。

なに？計算ができない？

それはまた別問題。計算練習をしましょうよ。

問題文をちゃんと読まない子供のやっちゃいがちなミス

問題文をちゃんと読まないと世の理の通りミスります。太陽は東から昇って西に沈むのであります。

単位を間違える

それ、メートルじゃなくてセンチメートルですから！ってか、あぁ、1/2ってメートルじゃなくて割合ですから！

馬鹿野郎！って言ったって直らないですからね。これ。

問題文を正しくトレースできていない

前回、速さの問題で説明しましたので今回も速さの問題で説明しようと思います。速さは入試頻出ですしね。

速さの問題ではこんな状況が問題文からひょっこり顔をのぞかせます。

「追いつく」

「電車を完全に追い越す」

「出会う」

「スタート地点で出会う」

「最初に出会ったあと往復して2回目に出会う」

「すれ違う」

「電車が橋を渡り終える」

「トンネルに完全に隠れた状態」

まだまだあるんでしょうけどこんなもんで今日のところはお許しください。

これ、全部絵にできますか？

絵にしなくたって、大丈夫ですって？あらまぁ、上級者でございますこと。絵を描く訓練をいっぱいやって状況が頭にパッと浮かぶようになってからですよ。絵を描かないのは。

大して訓練もしてないで解法を覚えたくらいのレベルなのに問題文を目で見てさささっとやるから少し難しくなると問題文の状況のトレースができないんですよ。

簡単な問題だったらまだいいです。

応用になったら問題文の条件も複雑になりますからね？頭の中だけで解こうとすると頭の処理能力を超えちゃうんです。

だから簡単な問題でもきちんと絵や図や図形や線分図やグラフ等にする。

これ、定説なのであります。

覚えた解法・公式でとりあえず数字の操作をする

とりあえず問題文で書いてある数字を拾ってきて、ああでもないこうでもないと足したり引いたり掛けたり割ったり。

だーかーら！問題文で与えられている条件をちゃんと自分で分かりやすい形に変換しましょうよ。

むやみに四則計算したって答えは出てきません。

問題を自分の分かりやすい形に正しく置き換えると解くまでの道筋が見えてくるものです。勘違いしていただきたくないのは解法や公式を覚えるのはとっても重要なんですよ。でも、そこまで行き着かなかったら意味がありません。そこまで行き着くためには問題文をちゃんと読む、つまり正しい条件整理が必要なんです。

問題を読めていない間違いとケアレスミスは違う

単位間違えたりとか、見当はずれの数字同士を掛けちゃったりとか、問題文とは違う状況を想像しちゃったりとか、こういうのってケアレスミスだと思われがちです。

「そそっかしいんです、うちの子」とよく言われたものです。

確かにそそっかしい子は多い。最後に足すべきところを引いたり、単位を間違えたり、一見するとケアレスミスのように見えます。はい、そういう時にドS先生の登場です。

「問題文を絵にしておしまいなさい！この醜い子豚め！」

と絵にさせてみると大抵できなかったりします。

ってかね、現象として現れているミスはケアレスミスのようですけど、本質は問題文を読めてないことですから。

時間かかってもいいから一所懸命、問題文を絵にしてみな！図にしてみな！

「とにかくゆっくりやれぇ！」

と言っておりましたところ心配そうな顔で別室から出て来てお茶の用意をするふりをするお母様。気が気ではございません。

「頭のイかれた家庭教師が来たのかしら？」

いやいや、こっちはイかした練習をさせてんだぜ！お茶は熱めでな！

同じミスでもケアレスミスの原因は頭のキャパオーバー。こっちは問題文が読めてない。同じように見えて根本は全然違うのであります。

【中学受験】ケアレスミスをなくす　原因と対策　原因は頭のメモリ不足

算数の条件整理とは何か

ここまで読んできていただいた「問題文を正しく読み把握する」ということ、これが条件整理です。別に特別なこと言ってないでしょ？でもこれ、結構できない子多いですからね。ってか面倒臭がってやらない。

簡単な問題だったらいざ知らず、ややこしい問題でしたらどれだけ正しく速く条件整理できるかはめっちゃ重要ですからね。

ちょっとロジカルシンキングをかじっている親御様は物事を図にしたり、絵にしたり、グラフにしたり、ピラミッドツリーにしたりして世の中の事象や人の話を分かりやすくしてません？

あれと一緒です。

問題文の事象を自分にとって分かりやすくして、そこからソリューションを導く手法。それが条件整理です。

簡単な問題だったら整理する必要なんかないじゃん、とか言っているとマジで足すくわれますからね。

慣れなさいって。簡単な問題で慣れましょうよ。

ってわけで、最後に一問、絵を使って条件整理しますから、そういうことね、というのを理解していただくと良いかと思います。

１辺150mの正方形の花だんの周りを太郎君と次郎君が回ります。太郎君はAを出発して、B→C→・・・と反時計回りに毎分100mの速さで、次郎君はCを出発して、D→A→・・・と反時計回りに毎分50mの速さで花だんを周回します。ただし、太郎君は次郎君と出会うごとに、回転の向きを変えることにします。ここで「出会う」というのは「2人が同じ地点にいる」という意味で使います。これについて、次の問いに答えなさい。【高槻】

（１）2人が初めて出会うのは出発してから何分後ですか。

（２）次に2人が出会うのは1回目に出会った後、何分後ですか。

（３）太郎君と次郎君が50回目に出会うのは、次郎君が何周目しているときですか。

引用　予習シリーズ算数6年上　第9回総合　チャレンジ②　P117

（１）2人が初めて出会うのは出発してから何分後ですか。

はいー、まずは絵を描きまーす。

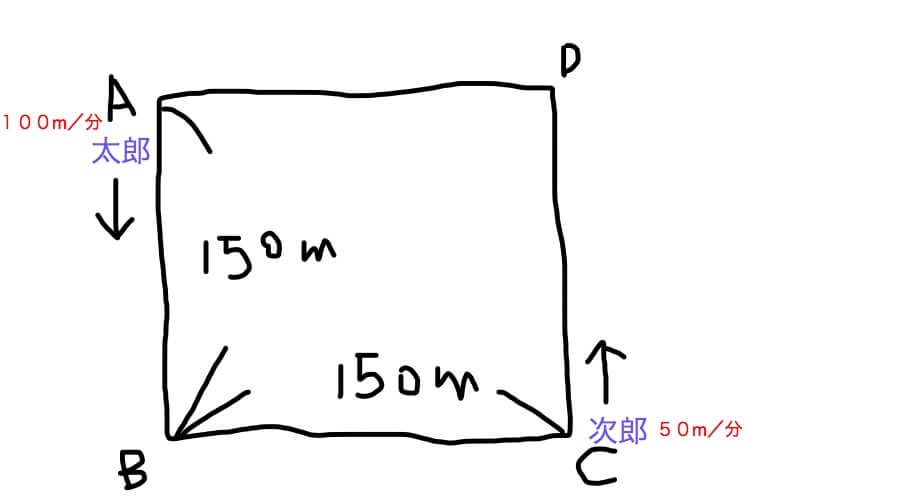
相変わらずヨレた絵ですね。誰か直線をキレイに描く方法を教えて欲しいものです。

こうやって問題文を絵にトレース（条件整理）いたしますと、すぐに（１）の答えが出て来そうです。

隠れた条件は、

「太郎君は300m離れた次郎君を追いかける」

なのであります。

したがいまして（１）は300÷（100ー50）＝6分

（２）次に2人が出会うのは1回目に出会った後、何分後ですか。

次、（２）行きますよ！こいつも絵で整理します。

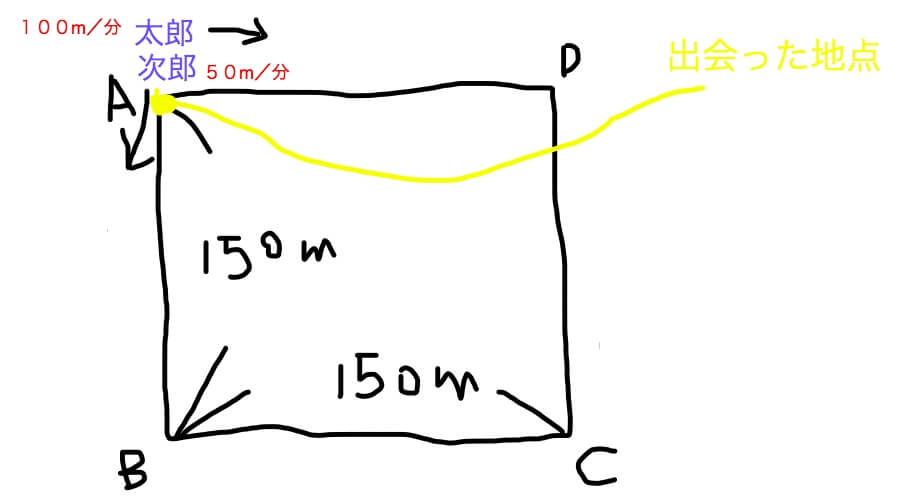
最初に出会うのは6分後ですからちょうどAの地点で二人は出会ったことになります。黄色の印をつけます。

そして太郎君は次郎君と出会うとなぜか逆方向に歩き出します。次郎君のことが嫌いなんでしょうか。

最初は反時計回りだったのが時計回りになります。

ということは（２）については「600mの距離を二人が正面から歩いて出会う」という隠れた条件が見つかりますよね。

したがいまして、600÷（100＋50）＝4分

（３）太郎君と次郎君が50回目に出会うのは、次郎君が何周目しているときですか。

はーい、では次に2回目の出会いの後どうなるかをまたド下手な絵で整理していきまーす。

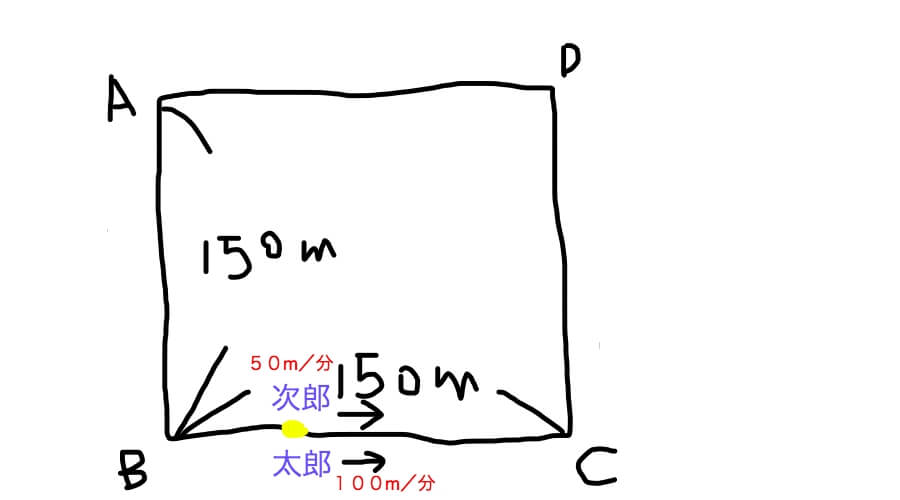
1回目の出会いから4分後ですから次郎君は200m進んでますよね。多分、上の図の黄色い点あたりで出会っているはずです。

で、太郎君はまたもやくるっと向きを変えますから、隠れた条件は「600mの距離を太郎君が次郎君を追いかける」なのであります。

次に太郎君が次郎君に追いつくとどうなるか分かります？

またもや太郎君は向きを変えます。

今度は「600mの距離を二人が正面から歩いて出会う」ととなります。

つまり、

最初の出会い以後、

隠れた条件１：「600mの距離を二人が正面から歩いて出会う」

隠れた条件２：「600mの距離を太郎君が次郎君を追いかける」

を繰り返します。

隠れた条件１の所要時間は4分、条件２は12分でありまして、こいつは規則性があります。

こんな感じ。

6分、4分、12分、4分、12分、4分、12分・・・・

最初の6分を除くと、周期は「4分、12分」の2つでありまして周期の合計は16分となるわけです。

最初の6分での出会いを除き、49回の出会いは「4分、12分」の周期になっていますから、

49÷2＝24・・・1

で、24回周期であまり１となります。

これを式にしますと、

24回×16分＋4分（50回目の出会い）＋6分（最初の出会い）

つまり、394分です。

次郎君は毎分50mの速さなので394分で19700m進みます。花だんは一周600mです。

したがいまして、19700÷600＝32あまり500

となり、32周が終わって33周目に突入しているのでありまして、答えは33周目です。

1周600mの花だんを33周も回って何をしたいのかさっぱり分かりませんね。多分、いじめですよ、三郎君の。あと、1周600mの花だんって馬鹿でかすぎです。花だんじゃなくて畑ですよ。

想像してみてください。一辺が150m、1周で600mの花だん。シュールですから。

ちなみに小学6年生算数上の解答をなくしてしまいましたので、本当に合っているかは分かりません。ま、多分合ってるでしょうけど。

お分かりいただけましたでしょうか？

基本問題から少々毛が生えると問題文だけじゃ解きにくいでしょ？

絵を使って条件整理すると、何を求めればいいのか分かりやすくなるでしょ？

たまたま今回は前回の流れから速さで説明しましたが、他の分野だって同じです。絵じゃなくても図とかグラフとか諸々で整理した方が分かりやすいんです。

絵や図、グラフなどの考える道具、つまりは思考整理の道具、予習シリーズの解説にいっぱい書いてますからしっかり勉強してくださいませ。

ところが成績が振るわないお子さんは2種類しかいないのであります。

予習シリーズを持っていないか持っていても大事なことが書いてあるのに気づかないか。

なんてこった、ジーザス。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介