【中学受験】予習シリーズとデイリーサピックスの比較と解説　5年算数自宅学習編

四谷大塚が誇る予習シリーズとSAPIXがぶっ放すデイリーサピックスは中学受験界の2大巨頭テキスト。さながらチャゲ＆飛鳥なのであります。

いえ、また間違えました。チャゲ＆飛鳥はコンビですので2大巨頭ではないですね。失礼いたしました。市川崑と今村昌平と言い換えておきましょう。

日能研を忘れていないかって？

忘れちゃいませんよ。ただ、紹介するにあたり、個人的にどうかなぁという部分がございまして省いているだけでございます。

さて、その2大巨頭の予習シリーズとデイリーサピックスでございますが、どっちも素敵なテキストです。身につけておくべきことが網羅されておりますし、何よりも思想が明白ですので使い方に迷うことがないのではないかと。

思想の違い？

ええ、思想の違いです。予習主義と復習主義。一言で言えばね。

でも、「予習主義と復習主義の違いでアール！」やらと言われても良く分かんないですよね。そんなん言われてもほんのちょっと困っちゃうジューシーフルーツですよ。

予習やら復習やらというのは表面的な話。

勉強とは何か、いいえ、もっと大げさに言っちゃうと学ぶとは何かに対する根本的なスタンスがこの二つのテキストでは違います。

勝手に定義しちゃいますよ。

予習シリーズとは学びの補助輪。

デイリーサピックスとは学びの一輪車。

さあ、これを読んでいる人も訳が分からなくなってきたところで、小学5年生算数で学習する旅人算を題材に学びの補助輪こと予習シリーズと学びの一輪車ことデイリーサピックスの違いを解説していきます。

小学5年生算数で成績停滞する理由

旅人算を題材にして2つのテキストを比較・解説していく前に、なぜ小学5年生の学習単元を取り上げるのか説明しておきます。

経験則で申し訳ないのですが、小学5年生にもなりますと成績上位と下位が固定されてまいります。それどころか小学4年生まではお立ち台でブイブイいわしてた子が小学5年生になってバブル崩壊することもしばしばございます。

算数はとくに顕著です。

内容が難しくなるし、応用的な内容も混じってくるからついていけなくなるんでしょ？

ってなお声もあると思うのですが、単に難しくなるからついていけなくなるんじゃなくて、私の感覚的には根本理解する習慣を怠っていたからついていけなくなる、という方が近い。

解法や公式を覚えて何となく当てはめで解いていたやり方が通用しなくなる、とでも言いましょうか。

で、成績が下降気味になってきているのに原因に気づかず、これまで通りのやり方をこれまで通りにやる、と。

それじゃあ成績が上がる訳がありません。間違った努力を何回繰り返しても間違った結果にしか到達いたしません。原理原則です。

勉強量が足りないのか、というとそんな単純な問題じゃないんです。腑に落ちるまで考えて自分の頭で納得し、どうしてそんな風に解けるのか人に説明できるようになるまでに至っていないんです。

根本原理が分かってないから基本とは少し違う問題が出てくると応用がきかなくてまるでだめ。

めちゃくちゃ問題解いて勉強しているように見えても、成績が上がらない根本的な原因、つまりスイートスポットに当たっていないから効果があんまりないってわけなんですね。

じゃあどうすんのか？というのが気になりますよね。

納得できるまで考えるんだYO！なんて精神論ぶちかまされても何のこっちゃです。

では一言で言います。根本理解をする、納得する、人に説明できるようになるためには自分が理解できる形や言葉に変換するんです。

そこまでできると応用も解けるようになります。

根本理解が大事そうなのは伝わりましたか？

さて、そんなに大切な根本理解。予習シリーズとデイリーサピックスではどう違うのか？

根本理解に達するまでの道筋が違うんです。

旅人算を題材に見ていきましょう。

小学5年生算数　旅人算を理解する

旅人算とは速さの問題の一種です。

純粋な速さのみの問題と異なるのは、追いかけられたり、追いかけたり、自転車で坂を登りながら徒歩の人との出会いを求めたり、2人で1人を追いかけたりと条件が複雑になる点です。いつ出会うのか、いつ追いつかれちゃうのかを算術で求めるんですね。

まるで「耳をすませば」みたいな世界の算数でございます。旅人算の舞台は聖蹟桜ヶ丘に違いありません。雫ちゃんと聖司くんの出会いが計算で求められるなんてワンダホーですよね。

これを四谷大塚では小学5年生の6月、SAPIXでは小学5年生の4月に習います。

では具体的な問題を見てみましょう。

よし子さんときみ子さんが600mはなれた地点にいます。よし子さんときみ子さんは向かい合って同時に出発したところ、2分後にはじめて2人の間のきょりは300mになりました。よし子さんの歩く速さを分速65mとすると、きみ子さんの歩く速さは分速何mになるでしょうか。

引用　小学5年算数　デイリーサピックス「旅人算」　より

では、こいつを2つの方法で解き、理解とはなんぞやということを説明していきます。

一つは式だけ。

もう一つは図を描きます。

式だけで旅人算を解く場合

（600ー300）÷2ー65＝85

よって答えは分速85m

中学受験経験のある親御様でしたら、上の式だけで何をやっているのか分かると思いますが、経験のない方は何のこっちゃという感じですよね。

これは出会いの旅人算で、こんな風に習うと思います。

「向かい合って進む2者の速さの和で距離を割ると時間が求められる」

要するに2人以上の人が同じ方向に進む場合の速さの問題です。速さのところで習う「はじき」の条件が複雑になったバージョンです。念のため申し上げますが物騒な方のハジキではありませんよ。

で、理解の上で大事なのは「はじき」の暗記じゃありません。リアルにイメージできるかなんです。

「はじき」だけでリアルにイメージできればそれに越したことありません。

でもね、もし「はじき」という公式や式だけ覚えて、向かい合って進むよし子さんときみ子さんが出会う様子を頭の中できちんと整理してイメージできないのだとしたら、もう少し理解に努めた方がいいでしょうね。

どうすると旅人算がよく理解できると思いますか？

とってもシンプルですよ。図を描くんです。

というか、理解を目的にした旅人算の家庭学習でしたら絶対に図を描くべきです。

図を描いて旅人算を解く場合

こんな図を描きます。これ通りじゃなくても構いません。自分が分かりやすければいいです。

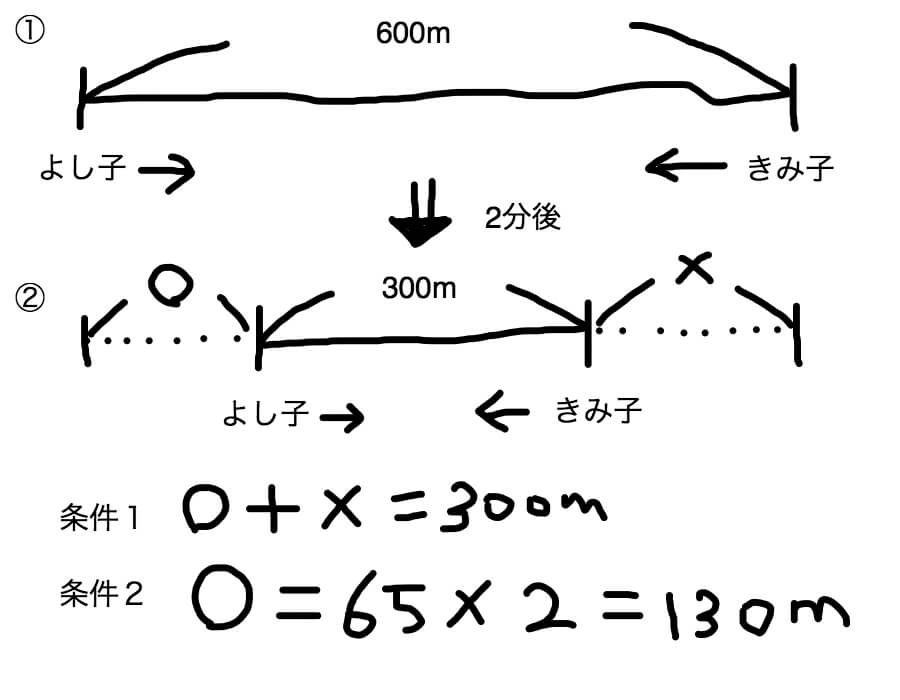
条件1、つまり二人が歩いたきょりは300mです。

条件2、よし子さんの歩く速度は分速65mですから、2分で歩ける距離は130mです。

条件1と条件2からきみ子さんの歩いた距離は300mー130mで170m（上図の×にあたる距離）となります。2分で170m歩きますので、170m÷2分で分速85m。

答えは分速85mです。

図にした方が理解しやすかったのではないでしょうか？

ちなみに、ここで伝えたいのは解き方なんぞではございません。そんなもんは塾でいっぱい教えてくれます。

本当に伝えたいのは、問題文を条件整理して具体的で目に見える「図」に落とし込むと問題文の世界がよく理解できるよ、ってことです。

旅人算の大抵の問題は「図」にするとよく理解でき解けるようになります。

逆に言いますと、条件整理して「図」という考えるための道具に落とし込む練習をしておかないといけませんね。なぜそのやり方で解けるのかという理解が曖昧になりますし、少し条件が複雑になると手に負えなくなってしまいます。

普通の人の頭は複雑なことをいっぺんに考えられるほど器用ではありません。だから考えるための道具、旅人算の場合でしたら「図」を使う。

ちなみに「図」にはグラフ、ダイヤグラム、線分図、図形など色々なパターンがあります。

これらの考えるための道具を使いこなせるように、一所懸命描く。練習です。

何を使って練習するか。

基本問題です。

徹底的に基本問題を使って問題を図に落とし込む訓練をするんです。

基本問題を「簡単！簡単！」とか言いながら覚えた公式を当てはめて、沢山問題を解いたって理解にはたどり着きません。

公式を使ってホイホイ解くのは理解してからです。

旅人算の場合でも図を描きまくって、頭にパッと図が思い浮かぶくらいになってから公式を使えばいい。

こんな簡単な問題で図を描くのは時間の無駄？

まあ否定も反論もしませんが、あとで後悔することだけは保証いたしましょう。

予習シリーズとデイリーサピックスの違い

はー、ようやく本題に入れます。長かった・・・。

予習シリーズの特徴は単元ごとに分かりやすい解説がついていることです。丁寧さたるや感涙ものですよ。

例題をベースにして、解くための考え方、根本的な理解のための考え方がめっちゃ書いてあるんです。

なぜなら予習を前提にしていますので、授業を受けずとも独学で理解ができるようなしっかりしたテキストになっているんですね。

旅人算の回では冒頭の解説や例題で図を使って、「どうして解法を使うと解けるのか」がたくさん書いてあります。

だったらすることはただ一つ。

解説や例題の解き方を真似しながら、理解に努めりゃいい。

私が上で書いたような図、予習シリーズではこれでもかと描いております。つまり、旅人算を根本的に理解するための方法論がしっかりテキストに書いてあるんですよ。

学びの補助輪と冒頭で書いたのはこうした所以。

予習して自分なりに理解し、その理解の確認と分からなかった部分を授業で解消する。めっちゃ再現性のある学習法です。

言葉悪いですけど、このテキストを使っていて予習しないのはアホです。RIZAP通ってるのに毎食ご飯3杯食べるようなものです。そりゃ成績なんか上がるわけありませんよ。

【中学受験】塾の予習と復習　目的と方法を押さえると学習効果は倍増する

対してデイリーサピックスは超簡素です。一つの単元で学ぶべき要素が見出しになっており、見出しに沿った問題が並んでいるだけです。

テキストというより、問題集みたいな趣です。

例えば、旅人算ですと「速さの単位」「速さの三用法」「同じ方向に進む」「スタート位置をずらす」「追いかける」「向かい合って出会う」「3人の旅人算」という7つの要素が見出しになっており、問題が並んでいます。

もちろん解答と解説はテキストに載っておりますが、予習シリーズの丁寧さとは比べ物になりません。

じゃあどうやって勉強して根本理解するんだよ！って思われるかもしれませんね。

ポイントは授業への集中と、ノートです。

めっちゃ集中して授業を受けて、あとで自分が理解できるようノートにしたためる。

家に帰ってからウンウン唸って「！」となる。

そして、自分でたどり着いた根本理解を手がかりに問題を解き、理解を自分のものにしていく。

宝物の在りかのヒントはくれますが、見つけるのはお前だよ、ってわけ。

でもね、自分で手に入れた理解は正真正銘の宝物です。

自力で学び理解する力が大きく求められるんですね。とても良い方法だと思います。万人向けじゃないですけど。

「ほうれ、一輪車に乗ってみろ！」とばかりに突き放し、転び、ぶつかり、よろめき、「ああ、そういうことか！」と気づいて自分の力で進んでいく。

学びの一輪車と言ったのはそういう理由です。

成績が伸びない子の特徴

どんな塾でも成績が良い子もいれば、成績が悪い子もおります。

なんでだろう、と思い悩んでいるかもしれませんが答えはシンプル。

当たり前のことをやっていないからです。

四谷大塚、もしくは四谷大塚系の塾に通っているのに予習やってないとか、マジでいますからね。

私はそういう子に解き方なんぞ教えませんでした。その代わり、どうして予習をやると良いのか、どうやって予習をやるのかを説いて、とにかく予習をやらせる。

分からない、とか言われてもやり方は教えませんでしたよ。「授業を受けて解決してこい」と言うだけ。

さすがに授業で解決できなかったことは教えましたけどね。

偏差値40くらいの子でしたら、それだけで月一で実施されるテストで偏差値60を超えた成績を取ってくる。

親御様にはたびたび感謝されましたけど、魔法を使ったわけでも特殊なことをしたわけでもありません。

当たり前のことをやらせただけ。

当たり前のことをやらない子が偏差値40〜60くらいにはひしめいておりますので、当たり前のことをやると一気に成績が上がる。ごくごく普通の話であります。

SAPIXに通っている子も同様。

ちゃんとノートを取ってない、集中して授業を受けてない、家に帰ってきてから理解のための時間を取らずにデイリーサピックスにずらっと並んだ問題をとにかく解こうとする。

それで成績が上がらないのは当たり前。

だって当たり前のことをやってないんですもの。旅人算の解法覚えて当てはめるだけじゃ応用効かないっすよ。

図を描け、どうして解けるのか説明しろ、図を描いて1個ずつ問題文の条件を整理して自分の頭で理解しろ。

SAPIXは下位の子を置いてけぼりにしてるとか、まことしやかに言う人いるじゃないですか。

とんでもない話です。

ちゃんと塾の基本方針を理解して勉強してないだけですよ。もしくは自力で勉強するのが向かない子なのか。

いずれにせよ人のせいにすんな、と言いたい。

理解する、とは何かを実践せよ

では最後に旅人算の問題と解法を提示しますから、式の意味を説明してみてください。

ちゃんと理解してたら式の意味を淀みなく説明できるはずです。

説明できなくても悲観しないでください。図を描いたらきちんと説明できるようになりますから。

それが理解です。

A地点とB地点の間は1800mはなれています。太郎君はA地点を、花子さんはB地点を同時に出発し、それぞれ一定の速さで両地点の休まずに何度も往復します。太郎君、花子さんの速さはそれぞれ毎分70m、毎分50mです。これについて、次の問いに答えなさい。

（１）2人がはじめて出会うのは、出発してから何分後ですか。

（２）2人が2度目に出会うのは、A地点から何mのところですか。

（３）太郎君が花子さんにはじめて追いつくまでに、2人は何回出会いますか。

引用　予習シリーズ算数　5年上　旅人算とグラフ（２）　往復の旅人算　より

（１）

1800÷（70＋50）＝15　答え15分

（２）

（1800＋1800＋1800）÷（70＋50）×70÷1800＝1あまり1350

1800−1350＝450　答え450m

（３）

{1800÷（70ー50）ー15}÷{3600÷（70＋50）}＝2・・・15

2＋1＝3

答え3回

式にすると意味不明ですよね？

これ、図を描くとぜーんぶ意味が分かって、どうしてこんな式を書けるのか説明できるんですよ。

予習シリーズを使ってようと、デイリーサピックスを使ってようとね。

大事なのはテキストでも塾でもございません。

塾の基本方針を理解し、基本に忠実に学び、しっかりと理解すること。

それだけです。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介