【中学受験】図形-円と正多角形　角度を求める基礎知識と補助線の引き方

今日は予習シリーズ小学4年生算数下巻の第3回「円と正多角形」をやっていきます。

ちなみに図形、苦手ですか？

中学受験の図形ははっきり言って難しいです。普通の中学生、高校生、あるいは大人でも解けない問題を小学生が解かなくちゃいけないのでありますから当然でございます。

けして「なんで図形が解けないの？」と聞いてはいけません。

解けないから解けないんです。理由なんかありません。強いて言うと難しいからです。

さて、「なんで図形が解けないの？」という疑問に似た苛立ちは時として誤った結論を導いてしまいます。

「図形にはセンスが必要なのかも？」

「確か図形脳とかいう言葉を聞いたことがある・・・」

「図形脳、いわゆるひらめきと思考力・・・、つまり右脳の力を引き出すといいに違いない！」

こうして右脳の力を引き出すべく、怪しげな参考書や塾の特別講座に手をかけてしまう人も少なくないでしょう。

実際は図形こそ知識とパターンの積み上げなんですけどね。

怪しげな参考書や塾に金払う前に、これまでやった図形単元の知識が本当に頭に入っているのかチェックした方がいいと思う次第であります。

実は毎回の図形単元で図形の性質に加えて、ちょっとしたテクニックを教わっているはずです。

知らない？

ちゃんと授業受けましょう。

例えば補助線の引き方。小学4年生はみんな苦手です。

あ、そうだ。しつこいようですが、今のところ算数については、私、予習シリーズを使ってる小学4年生向けに書いてますからね。そんなん習ってねーよとかやり方違うんだけど、というクレームは受け付けません。

補助線の引き方にはパターンがあります。

しかしながら、補助線の引き方のパターンを分類して教えてくれる塾の講師はあんまりいません。どうしてなんでしょうかね。

私が、30年前に補助線の引き方のコツを聞きにいったとき

「補助線は答えを導き出せるところに引くんだよ」

と、やさしくアドバイスをくれた塾の先生は今頃元気にしてらっしゃいますでしょうかね。

これじゃまるで「バッティングのコツは来たボールをパーンと打つんだ！」と喝破した国民栄誉賞の人の教えみたいです。

さて、また脱線してしまいました。

図形の問題を解くのにひらめきはあまり必要ありません。ましてや右脳トレーニングなんかやらないほうがいいです。

正確な知識の積み重ね、これが一番大事。

と、作問で苦労していらっしゃる私立の数学の先生が言っております。

「これとこれとこれを組み合わせたら解けなさそうな問題ができるゾ、ウヒヒ！」

私立の数学の先生がみんなひらめく人だと思ったら大間違いです。大抵は普通の人です。

ひらめき問題を作れる人なんてそう多くはありません。

ひらめきが必要なのって筑駒と灘くらいじゃないスか？

今回は何を学習する？図形の問題を分類する

まずは図形の問題を分類しましょう。

図形は大きく分けて、平面図形と立体図形の2つに分けられます。

予習シリーズの小学4年生算数下巻第3回でやっているのは平面図形に分類されます。

平面図形をさらに分けると、

1.長さを求める問題

2.面積を求める問題

3.角度を求める問題

平面図形は大きく分けると上の3つに分けられます。

で、ですね、今回の単元は角度を求める問題と長さを求める問題が出てまいります。

なんでこんな分類をしているのかと言いますと、学習単元ごとに「何を学習するのか」を意識するのがとっても大切だからです。

今回は円と多角形の概念を覚えながら、平面図形の角度を求める問題と長さを求める問題を学習する回です。

平面図形の角度に関する知識

1学期、それから夏期講習でも平面図形の角度の求め方やりましたよね。知りませんがやったはずです。

これまで習った平面図形の角度に関する知識で大事なのは以下のとおりです。

1.1回転はの大きさは360度である

2.半回転の大きさは180度である

3.三角形の3つの角の大きさの和は180度である

4.対頂角の大きさは等しい

5.同位角の大きさは等しい

6.錯角の大きさは等しい

7.外角の定理

8.二等辺三角形の三辺のうち、長さが同じ二辺ではない辺に接する二つの角の大きさは等しい

9.正三角形の角の大きさはすべて等しい

9個もあげてしまいました。今まで習った角度に関する知識で大きなところはこんなもんです。（こまごまあげると他にもありますが）

これ、全部覚えてますか？そして正確に説明できますか？

これらを覚えていて、かつ理解してないと今回の単元ははてなマークでいっぱいになることでしょう。

何回も書きましたが算数（数学）は積み重ねです。

今までやったことがフワフワしていたら、関連する新単元の理解もフワフワするんです。

図形はセンスじゃありません。苦手なのはセンスがないからじゃありません。

単なる知識不足。

もしくは、

練習不足。

悲観することはありません。センスの一言で片付けられたら何をしたらいいのか分かりませんもの。知識不足や練習不足なら補えます。

上にあげた9つの知識は予習シリーズ小学4年生算数上巻3回と8回にちゃんと書いてあります。

今回の単元でワケワカランとなっておりましたら、上巻3回と8回を復習することをおすすめいたします。

対頂角、同位角、錯角、外角の定理のおさらい

いきなり今回の内容に入る前に上であげたうちの4つだけおさらいしておきます。

対頂角の大きさは等しい

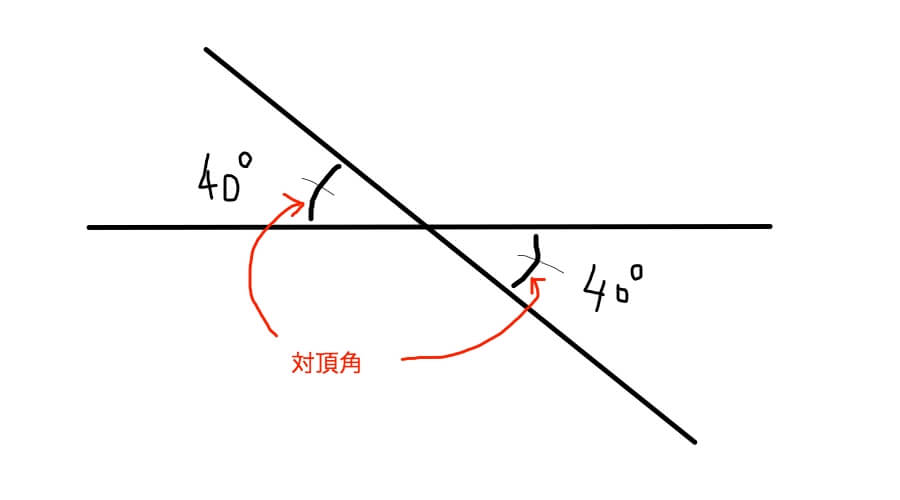
2本の直線が交わったときにできる角のうち向かい合った角のことを対頂角と言い、大きさは等しくなります。

上の図の40°の角が対頂角です。

同位角の大きさは等しい

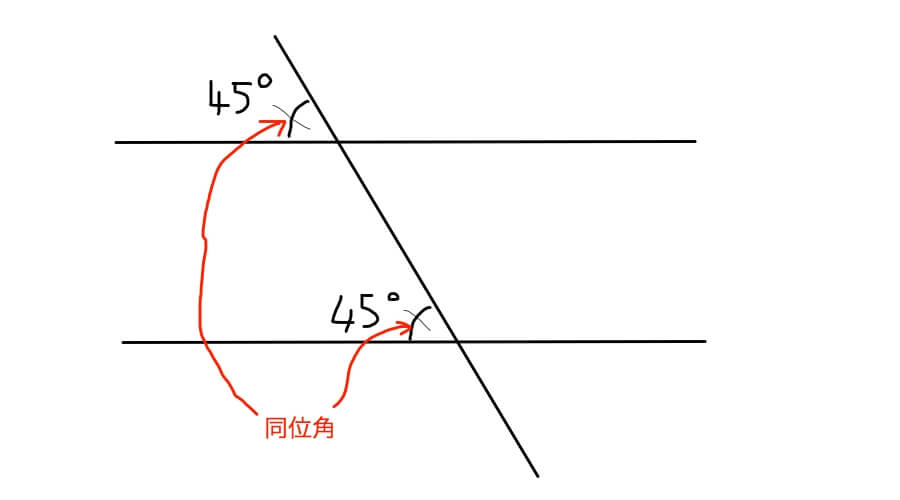
2本の平行な直線に交わる直線を引いたときに、同じ位置関係にある角のことを同位角と言い、大きさは等しくなります。

上の図の45°の角が同位角です。

錯角の大きさは等しい

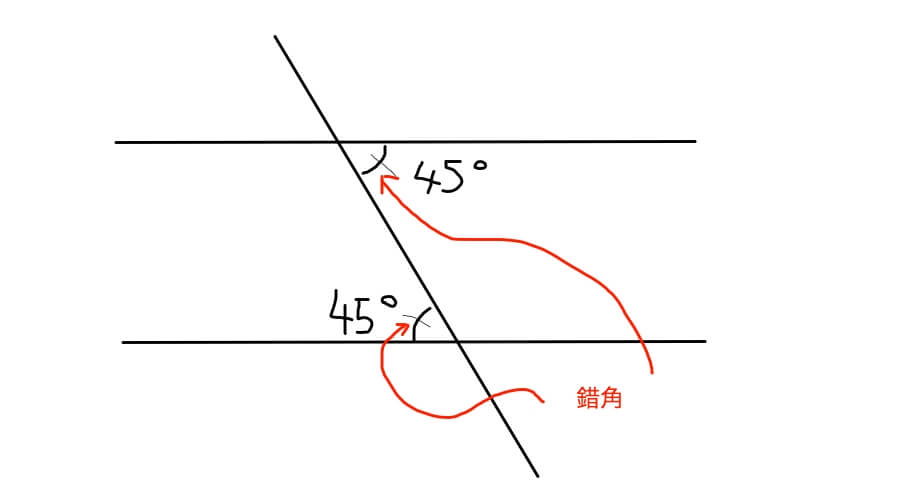
2本の平行な直線に交わる直線を引いたときに、平行な直線の内側にできる互い違いの角を錯角と言い、大きさは等しくなります。

上の図の45°の部分が錯角の関係になります。文字で説明すると分かりにくいので図で位置関係を覚えてしまいましょう。

ちなみに45°の角の向かいにある内側の角（135°）も錯角となります。

外角の定理

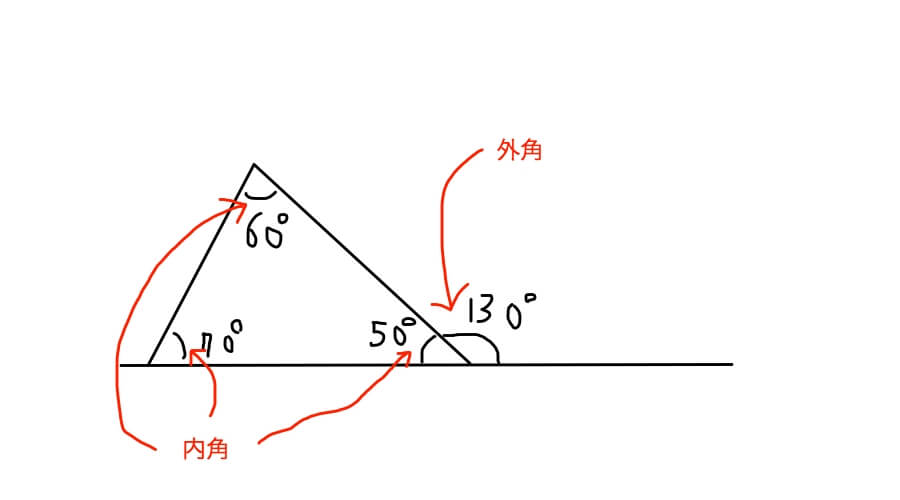
三角形の3つの内角（角A、角B、角Cとする）のうち、角Aと角Bの和は角Cの外角の大きさと等しくなる。

ただし、これ、角Cと角Cの外角を足したときに180°になることが条件です。

上の図でいうと、50°の角とその外角（上の図では130°の角）を足して180°にならないと通用いたしません。

つまり、三角形の辺からまっすぐに直線が伸びていることが条件になります。ぐにゃぐにゃだったり、屈折してたりするとだめです。

円と正多角形の性質

ようやく今回のお話に入ります。

円の性質と正多角形の性質ですが、これは覚えてしまいましょう。絶対に必要な知識です。

円の性質

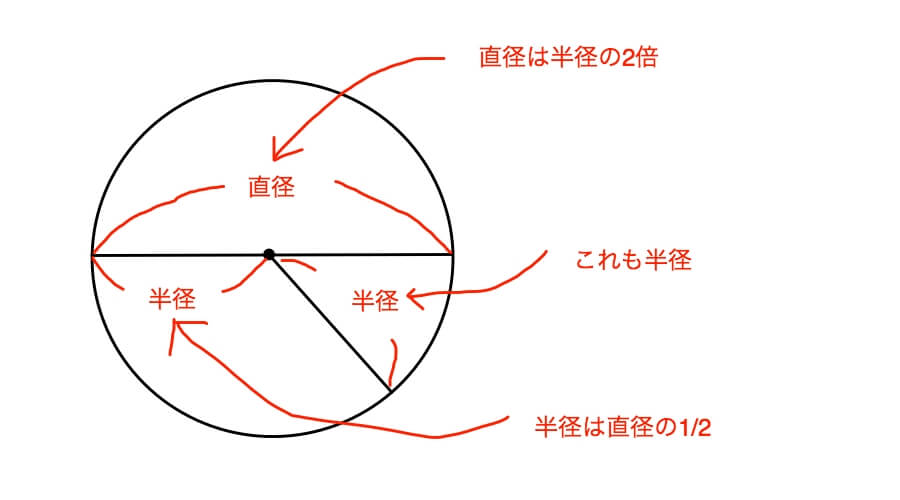
円の直径とは円周上の一点から円の中心点を通って、反対側の円周上の一点まで引いた直線の長さのことを言います。

円の半径とは円周上の一点から円の中心点までの直線の長さのことを言います。

上の図で書きましたように直径は半径の2倍、半径は直径の1/2という関係が成り立ちます。

ここまでは大丈夫ですよね。

正多角形の性質

正多角形を書きたかったのですが、私の描画技術では無理でしたので言葉で説明します。

ま、ちゃんと予習シリーズに書いてあります。

1.正多角形の内角の大きさはすべて等しくなる

2.正多角形の一辺の長さはすべて等しくなる

この2つです。

で、円の中にすっぽり正多角形がおさまる図形とかが出てくると、

3.正多角形の頂点から円の中心点を直線で結ぶと、中心点は頂点の数で等分される

ということが言えます。

図形は知識とパターンの積み上げで解く

はぁ、やっと本当に書きたかったことまでたどりつきました。

今回の図形のお話でも、いろんな知識が出てきましたね。

円の性質、正多角形の性質、円と正多角形を組み合わせたときの性質。

こういった知識をベースにしてそれぞれの性質に着目して解くのが図形の問題です。

図形が苦手なお子さんは往々にして基礎的な知識や、どのように着目するのかというパターンが抜けております。

三角形の回では、同じ長さの辺や同じ大きさの角を見つけて解いていきましたよね。場合によっては補助線を引いて。

【中学受験】小学4年生予習シリーズ算数　第8回「三角形の角」をマスターする

今回もとっておきのテクニックがありまして、それは「円の中心に点を打つ」です。

それだけ？

はい、それだけです。

そんなに激しい点じゃなくて結構ですよ。ええ、普通の点で大丈夫です。

点は打ってあるけど解けない、ですって？

あぁ、じゃあ次は半径に注目しましょう。

円の中心に点を打ち、半径に注目する。あるいは打った点から半径を引いてみる。

私、上の方で補助線がどうやらこうやら話しましたが、円が出てくる問題では中心に点を打って、中心点からいい感じに半径を引いてみると、不思議なことにそれが補助線になっていたりします。

「いい感じに半径を引く」なんて我ながらなんとアバウトなんでしょう。

こんなアバウトな言い方をしたのは問題によって、どのように半径を引いたらいいかが異なるからです。

たとえば、

正三角形を作るように半径を引く

とか、

二等辺三角形を作るように半径を引く

とか、

角を二等分するように半径を引く

とか、いろんなパターンがあります。

問題がでてきたときに、

①「どこが分かれば求めるべき長さや角の大きさが分かるのか？」を考えて、

②「円の中心に点を打って」軽く問題をしばいたあと、

③「中心点から半径（直径でもいいっス）を引いて」分かりたいものを分かるようにする、

というのが円が出てくる平面図形をやっつける作法です。

上の3段階のうち、②は機械的にできますよね？

問題は①と③です。

これだけは機械的な作業ではなく、いろいろなパターンがあるから「こうやればいい！」と断言できないんです。

で、このパターンなるものはたくさん問題を解いて身につけるのが近道です。

一方で詰め込み式に頼らずに図形的思考力を身につけて解くのを推奨する人もいます。

どっちがいいのかは知りません。

が、前者は再現性が高く、後者は再現性が低いです。

前者は特訓すれば身につく可能性が高いですが、後者は特訓して身につくこともありますし、身につかないこともあります。

どちらをとりますか？

私は再現性の低い方法論を推奨するのは無責任だと思ってます。

もちろんそうでないと考える人もいるでしょう。このへんはスタンスの違いですから、良い悪いの問題ではありません。

最後に円と正多角形の問題を解く

では、ああやこうや言ってきましたが実際に問題を解いてみましょう。

と、予習シリーズを見ますと殆どの問題が円の中心に点が打ってあるじゃないですか！

OUCH！

あぁ、良かった。練習問題の最後の問題だけ点が打ってないですね。これでいきましょう。

問い

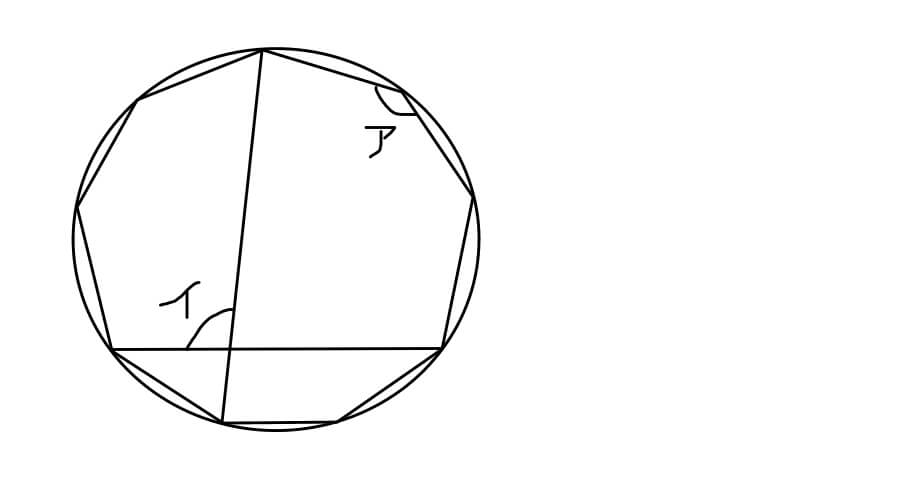
右の図は、円の中に正九角形をかいたものです。

これについて次の問いに答えなさい。

※注　ここでは「右の図」は「下の図」と読み替えてください

（１）角アの大きさは何度ですか。

（２）角イの大きさは何度ですか。

引用元　予習シリーズ算数　4年下　第3回「円と正多角形」練習問題より（四谷大塚出版）

ほぼフリーハンドで書きましたので残念ながら正九角形にはなりませんでした。まあそれはいいでしょう。

（１）は楽勝ですね。

（9ー2）×180÷9＝140

答え　140°

正多角形の一つの内角の大きさを求める公式は↓でしたね。

（頂点の数ー2）×180÷頂点の数

なに？そんなの書いてない？

・・・えーと、確かにテキストに書いてませんね。

じゃあ、気を取り直しまして中心に点を打って半径を書いてしばきながらいきましょう。基本通りにね。

角アの大きさは中心（360°）を9分割した角度を求めて、円の半径が同じ長さであることを利用して二等辺三角形を作れば求められそうです。

じゃあ、いてこましていきます。

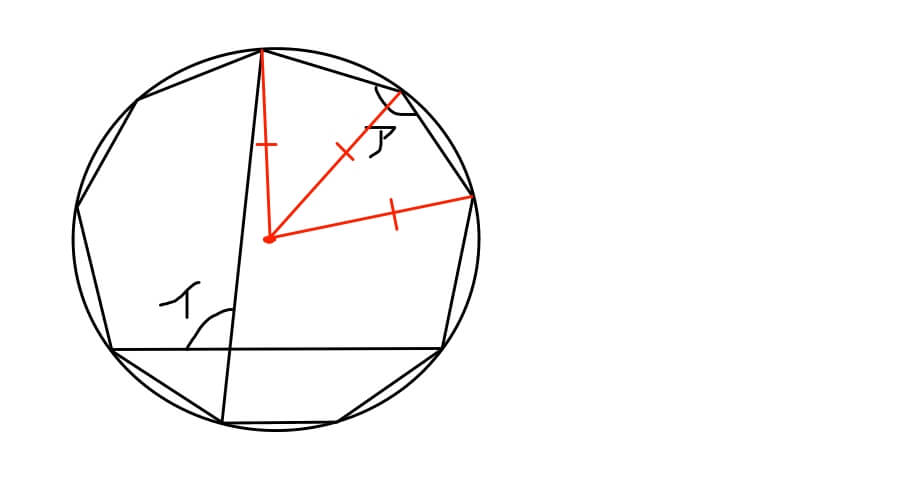
赤い点が中心点、赤い点から円周まで引いた直線が半径です。

半径の長さは一緒ですから、ご丁寧に引いた3本の直線はすべて同じ長さになります。

すると二等辺三角形が二つできていることに気づきますね。

さぁ、チャンス到来ですよ。リーチかかってます。

正九角形ですから、中心点のところの角の大きさは

360÷9＝40°

と求められます。

すると、この二等辺三角形の同じ大きさの二つの角は

（180ー40）÷2＝70°

と求められますね。

で、角アは70°の大きさの角が二つ合体したものですから

答えは、

70×2＝140°

と求められます。

公式を使わないと面倒ですね。まあ、基本に忠実にいきましょう。

では次。（２）です。

この問題は下のように青色の補助線を引いて考えます。

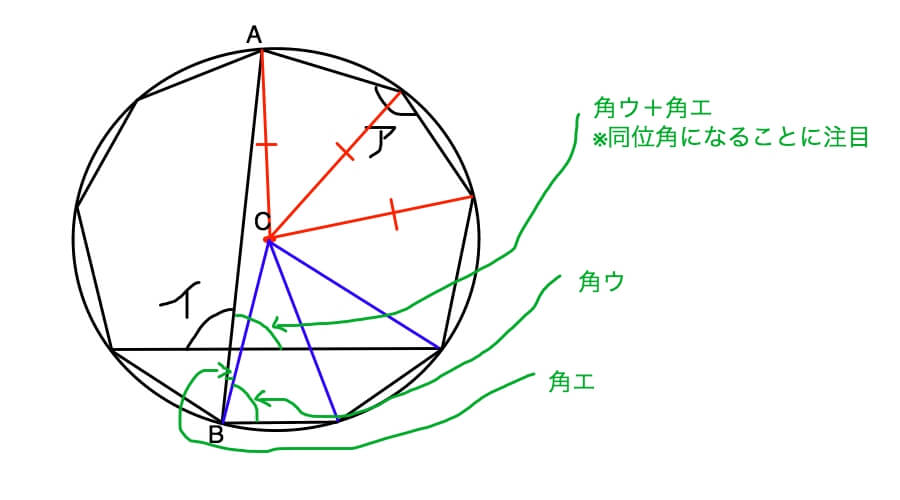
上の方で、円が絡む正多角形の問題では中心点からとりあえず半径を引くと、不思議なことに補助線になっている、と申し上げましたね。

ですから、とりあえず青色の半径を3本引きました。このへんは訓練していくと、「とりあえず」ではなく意図的に狙って補助線を引けるようになります。

すると、新たに角ウと角エができました。

で、ここで前習った知識である同位角を使います。

「角ウ＋角エ」と同じ大きさの同位角が角イの反対側にできるではありませんか！

ということは角イは、

180ー（角ウ＋角エ）

で求められますよね

では角ウを求めましょう！っつーか、これ（１）で求めましたよね。70°です。

次に角エを求めます。

三角形ABCの細っこい角です。説明のためにA、B、Cとそれぞれの角に名前をつけて、三角形ABCを作りました。

この三角形ABCの辺ABと辺ACは円の半径ですから長さが同じです。つまり二等辺三角形です。

ということは角BACと角ABC（角エのこと）は同じ大きさになりますよね？

つまり、角ACB（でかい角）が求められれば角エは求まります。

角ACBは40°の大きさの角が4つ集まった角です。

だって、正九角形の辺が4つありますよね。

ですから40×4＝160°と求められます。

すると角エは（180ー160）÷2＝10°と求められます。

角ウと角エを足して180°から引くと、角イが求められますから、

180ー（70＋10）＝100°

答え　100°

となります。

まだ習っていない方法を使うと、この他に3つくらい解く方法があります。

上の解き方は今まで習ったことしばりで解いてます。

図形の単元で重要なこと

さて、ここで言いたいのはこの問題の解き方ではありません。

中心に点を打って、半径をいい感じで引いて、これまで習った方法を利用すると問題が解けるってのを知ってもらいたいんですよ。

とくにこれまで習った方法を利用するってのがミソです。

同位角を忘れてたら解けませんよね？この問題。

図形を解くコツは正しい知識の積み重ねと最初に申し上げましたが、逆に言うと正しい知識と積み重ねがないと解けないんです。

円と正多角形の基本的な性質。

円と他の図形を組み合わせた問題が出たら、円の中心に点を打ち半径を書くというテクニック。

こういった基本理解とテクニックの上に、習った知識を利用して解くのが図形の問題です。

難しそうに感じるかもしれませんが、習った知識の利用の方法にはパターンがあります。

いっぱい問題を解けば「あぁ、このパターンね」っていう天才みたいにお子さんがつぶやいて度肝を抜かれることでしょう。

少なくともいっぱい問題を解いてパターンを体に覚えさせる方が、過去の知識を総動員して思考力に頼って解こうとするより、よっぽど再現性があると思いませんか？

なに？筑駒と灘を狙うならパターンじゃ通用しない？

それ、全中学受験生のうちのいったい何％のお話なんですか？

そんな本質的な思考力がある子はごく一握りです。

詰め込みは悪で、本質的な思考力を養うべきだという人はきっと頭が良く生まれてきたんでしょうね。

羨ましいことです。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介