【中学受験】推理算　数直線・魔方陣・総当たり戦・順位表の学習方法

さ、予習シリーズ小学4年生算数下　第7回の「推理して解く問題」でございます。

この回はそんなに困らないはずですので、抜かそうと考えておりましたがご質問をいただきましたので一応書いていきます。

と、最初から手抜き宣言を出しておきます。

だって、推理ってやり方を覚えてるか覚えてないかだけなんですもの。

なんか張り合いがない気がしちゃうんですよ。

この分野は論理的に考えていく、要するに順を追って考えていくと答えが出ます。

論理的思考を養うための手法を学ぶ、とも言えます。

聞こえはいいですが、ツールと手順の暗記でいけちゃう分野でもございます。

順番の問題が出てきたら数直線を書く。

魔方陣の問題が出てきたら穴を埋めていく。

勝ち負けの問題が出てきたら勝敗表を書く。

順位の問題が出てきたら順位表を書く。

これだけです。

もちろん、ツールを覚えるだけじゃなくて、手順はありますし、考え方のコツもあります。

が、前提として「この問題に対してはこのツールを使う」と覚えておかないと解けません。

もし、推理の問題が苦手なら「論理的思考がー」とか「発想力がー」とか言う前にやり方を覚えているのか疑った方がいいでしょうね。

ちなみに予習シリーズですと小学4年生の秋くらいにやりますが、サピックスでは春期講習で学習します。

サピックスは予習シリーズより半年くらい早いわけです。ちなみに予習シリーズ小学4年生算数下巻の第6回「割合」はサピックスでは5年生でやります。

塾によって早く学習する単元があったり、そうでなかったりしますね。

個人的には推理はサクッと春期講習や夏期講習でやっちゃってもいいんじゃないかと思ってたりします。

なぜなら、

推理は中学受験で学習する算数の中では独立した分野です。

算数は積み上げ型の教科ですが、推理について言うと積み上げではありません。

やり方を覚えて手順に則って解くだけの独立した分野です。

推理で学んだ内容が他に影響したり、あるいは他で学んだ内容が推理に影響することは多くありません。

したがって、中学受験勉強が本格化して間もない小学4年生の春でもやり方さえ覚えればサクサクいけます。

が、サピックスでは5年生で学習する「割合」はそうはいきません。

小数、分数の概念、割り算、かけ算の概念を分かってからでないと「割合」には入れません。

四谷大塚が、なぜこんなところで推理をぶっこんできたのか甚だ疑問ですが、ぶっこまれてしまった以上仕方ありません。

ぶっこまれたらぶっこみ返す・・・、3倍返しにしてやりましょう。

推理の解法パターン4つ覚えときましょう

推理の問題の基本はツールの利用です。

つまり、問題を見てどんなツールを利用するのか特定できないと話になりません。

問題のパターンは4つ覚えておくといいでしょう。

1.大きい、小さいを推理する（順番）

2.魔方陣

3.勝敗表

4.順位表

1.大きい、小さいを推理する場合

大きい、小さいを推理する場合は数直線を使います。

↓な感じの問題です。

A、B、C、Dの4人の年齢を比べたところ次のようになりました。

Bの年齢が10才としたとき、A、C、Dの年齢を求めなさい。

・AはBくんよりも年下。

・BとCは5才はなれている。

・CはDよりも9才年下。

・AはCよりも2才年上。

この手の問題が出てきたときは必ず数直線を引く。

マジでこれだけっす。

一応、書き方のルールだけ決めておきましょう。

・数直線の左から右にいくほど大きくなる

・数直線の下にA、B、C、Dなど登場人物（モノ）を書く

・数直線の上に数字を書く

あとは問題文の条件を数直線に書いていくだけです。

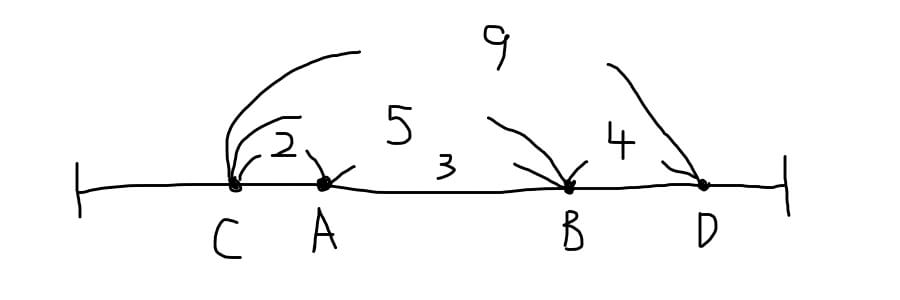
・AはBくんよりも年下。

→AがBの左になるように点を打ち、下にA、Bと書きます。・・・①

・BとCは5才はなれている。

→BとCの上に5と書きます。・・・④

・CはDよりも9才年下。

→C、A、Bよりも右に点を打ち、下にD、上に9と書きます。・・・③

・AはCよりも2才年上。

→Aの左にCの点を打ち、下にC、上に2と書きます。・・・②

書き方のコツは、確定しているところから点を打つ。

たとえば「5才はなれている」と書いてあっても、年上なのか年下なのか分からない場合はいったんとばして、点を打てる条件から先に処理していきます。

1 2 3 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介