【中学受験】約数、約数の個数、素数、最大公約数と連除法（はしご算）

おいおい、ちょっと待てよ予習シリーズ、つまり株式会社ナガセ。

なんで連除法の例で素数じゃない数で割ってるんですか。（参照：新版予習シリーズ4年生上　算数P140）

え？巷では連除法では素数じゃない数で割ってもいいとか言われている？

あー、世間で言われているかどうかは関係ありませんね。

連除法では素数で割れ、以上。

まぁ、最大公約数を求めるだけだったら素数じゃなくてもいいんですよ。でも、「これは最大公約数を求めるときだけですよ」みたいな注釈が一切ありません。

ってわけでいきなり株式会社ナガセへのクレームで始まった約数の分野です。

前回の等差数列に比べるとだいぶ取り組みやすいので安心してしまいがちですが、この単元、数の性質を学んで感覚を身につけましょう、って分野です。

ナメてると苦労します。

特殊算はやり方がある程度決まっていてまずは覚えましょう、って感じですが今回の単元で学ぶ約数は、数の性質や感覚を身につけるのが主目的です。

だから難しいんですよね。

約数や公約数を求めるにも色々なやり方や便利なテクニックはありますが、覚えるだけじゃ通用いたしません。

何を意識しながら学習していった方がいいのか、相変わらずの独自性でかましていこうと思います。

約数とは

約数ってのは、ある数を割り切れる整数のことです。

例えば、24だったら、

1、2、3、4、6、8、12、24

で割れますよね。

これが約数。

言うまでもないって？

まぁゆるりと聞いてくださいよ。

ここまでは簡単。

あ、ちなみに2桁の数の約数だったらいちいち計算式を書かなくても列挙できるくらいにはしておいた方がいいですよ。

ある数の約数を求めるコツはいくつかあります。

1.偶数かどうか

2.3の倍数かどうか

3.5の倍数かどうか

4.9の倍数かどうか

5.平方数かどうか

1.偶数だったら必ず2で割れます。

2.3の倍数は全部の桁を足して3で割り切れる数です。（例：129の1と2と9を足すと「12」。12は3で割れるから129は3の倍数）

3.5の倍数は1桁目が5か0で終わる数。

4.9の倍数は全部の桁を足して9で割り切れる数です。（例：279の2と7と9を足すと「18」。18は9で割れるから279は9の倍数）

5.平方数の約数の個数は奇数個になります。逆に平方数以外は偶数個になります。例えば42の約数は1、2、3、6、7、14、21、42で8つ。平方数である64の約数は1、2、4、8、16、32、64の7つ。

上の1〜4までは約数を探し出すテクニックです。

で、最後の5。なんで約数が奇数個か偶数個になるかを知っておいたほうがいいかというと、

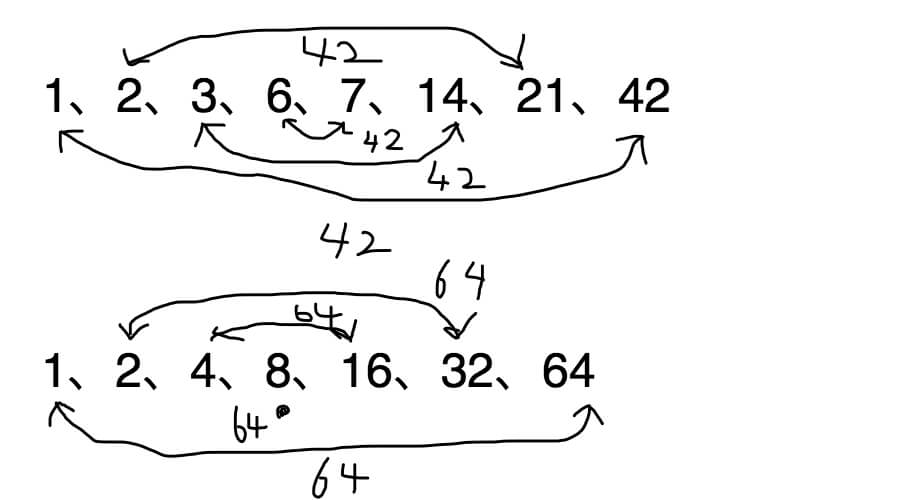
こんな風に平方数以外の約数は最初の数と最後の数をかけるとその数になり、最初から2番目の数と最後から2番目の数をかけるとその数になります。で、隣り合う数同士をかけてその数になったところが真ん中。

42だったら6と7が約数として見つかったら真ん中発見。64のような平方数でしたら、8が出てきたら真ん中発見。

平方数は真ん中の数を二乗するから約数の個数は偶数個にならないんですね。

真ん中を見つけるといいことがあります。

オラオラ頑張ってそれ以上大きな約数を見つける努力は全く必要はなくなり、真ん中よりも小さい数で順番に割っていけば約数が求められます。

ちなみに平方根が20くらいまでの平方数は覚えておいた楽です。

1、4、9、16、25、36、49、64、81、100、121、144、169、196、225、256、289、324、361、400

ってね。階差数列になってますから覚えやすいかと。

約数の個数

ここまでが小4の範囲。約数の個数を求めるには、小4までは上の要領で約数を列挙して数えていけばいいです。

ところが問題は小5で習う約数の個数の算出方法。

↓のようなキテレツな方法が出現いたします。

「素因数分解し、指数に1を足した数をかけると約数の個数になる」

ガッツ石松くらい何言ってるのかさっぱり分かりません。

具体例をあげます。

24の約数の個数を求めるときにまずは素因数分解をします。

2×2×2×3

2の3乗に3の1乗をかけたものになりますね。では、指数に1を足したもの同士をかけあわせます。

（3＋1）×（1＋1）＝8

で、24の約数は8個と求められます。

なんでそうなるの？って普通思いませんか？

おたくの聡明なご息女、ご子息だってそう思うに違いありません。

一応テキストでは理屈が説明されておりますが、テキストだけ読んで合点するのはアホか秀才くらいです。

中学受験の算数ってのは中学や高校で公式を使って解く問題を、本質的な理解だけで解いていく営みであります。

その点、このガッツ石松の一発ギャグみたいな公式を覚えて解くのは本質的じゃありません。

塾の先生もおそらく一所懸命理屈を教えてくれると思いますが、往々にして意味不明の状態で帰ってきます。

生兵法は大怪我の元と言いますが、意味不明な公式を覚えて解くと複雑骨折いたします。

ちなみに上であげた一発ギャグは場合の数を使うと納得できるようになります。

まず、1はどんな整数でも約数になりますよね。

だから、「2×2×2×3」は素因数が2と3しかないように見えますが約数として1も含まれます。

場合の数では、あるパターンの数とあるパターンの数をかけると全部の場合の数が求められますよね。

ですから、2のパターンを考えますと、「2を使わない（1が暗躍しています）、2を1個かける、2を2個かける、2を3個かける」の4パターンあります。

3のパターンは「3を使わない（またもや1が暗躍しています）、3を1個かける」の2パターンです。

それぞれのパターンをかけると4×2で8となり、場合の数は8になります。

ざっくり言いますと、1という素因数分解に現れない数が存在するので1を足すってわけです。

この理屈が樹形図とともに頭に思い浮かぶようになってから公式を使っていただきたいと切に願っております。

素数を覚えちゃいなよYOU

素数です。

そもそも「1以外で、1とその数自体でしか割れない数が素数です」とか言われても小学4年生にとっては何のこっちゃです。

なので、体で覚えます。意外と大事ですよ、体。

100くらいまでの素数は瞬時に分かるようになると、とっても楽です。

訓練法はこうです。

「はい、1は？」

「あぁ素数！」

「違う！1は素数じゃない！」

「あぁ！」

「2は？」

「素数！」

「3は？」

「素数！」

「4は？」

「素数！」

「ちげーよ！2で割れるだろがー！」

「あぁ！助けてママン！」

という具合にひたすら100までの素数を体に覚え込ませるといいですね。

教育虐待じゃなくて素数虐待ですからコンプラ的にぎりぎりセーフです。

素数を覚えると素因数分解ができるようになりますし、連除法でも役に立ちます。

公約数、最大公約数、連除法

公約数と最大公約数を求めるには連除法を使えばいいです。

ルート記号をピンホールカメラで見ると連除法のアレになります。時々マジでどうでもいいことを差し込んでいきますよ。

さて、連除法をやってみましょう。48と72の公約数と最大公約数を求めます。

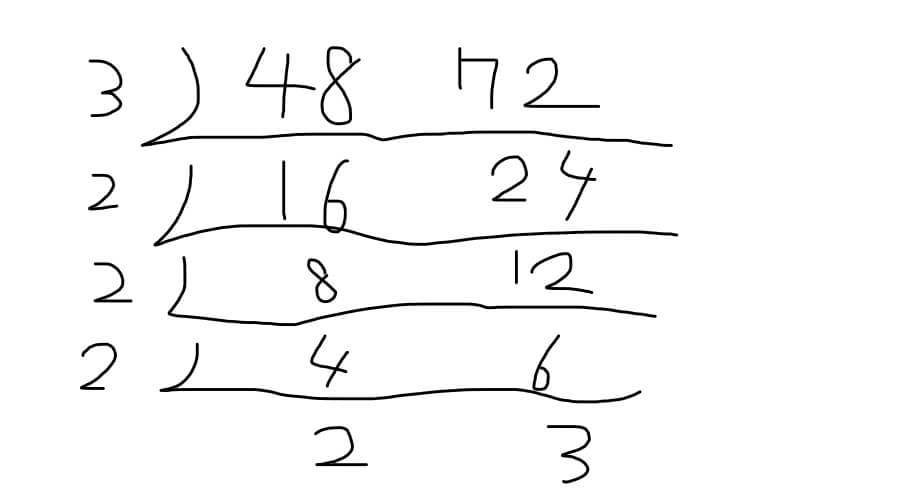
どうです、左側が美しい素数ですよ、奥さん。

最大公約数は3×2×2×2で24、です。

次は約数の個数を求めてみましょう。連除法で公約数の個数を求めるコツは場合わけです。

・かけ算をしないパターン　1、2、3

・2個のかけ算をするパターン　2×2、2×3

・3個のかけ算をするパターン　2×2×2、2×2×3

・4個のかけ算をするパターン　2×2×2×3

全部数えていくと8パターンになります。つまり約数は8個。

え？なんで最初に6で割らないのかって？

公約数の数を求められないからですよ。

公約数の個数を求める問題だって連除法で求めますからね。

鼻垂らした小学生に

「いい！公約数の個数を求めるときは素数ヨ！最大公約数だったら素数じゃなくていいから！場合分けして覚えてネ！」

なんて教えてうまく場合分けできますかね？間違えのもとです。

どんな問題でも通用するやり方を一つ覚える方が圧倒的にミスが少ないんです。

素数で割れば公約数や最大公約数を求める問題の両方に対応できます。

ちょっとの手間を惜しんで連除法で素数以外の数字で割るのはマジでファックな行いです。

ちなみにリングのロープをかいくぐってガッツ石松が現れましたので、約数の数を求めるガッツ石松法が公約数の個数を求める場合でも通用するのかも見て行きましょう。

連除法の左側は、

2×2×2×3

となっていますね。

ガッツ石松法を当てはめると、

(3+1)×(1+1)＝8

と出ます。

つまり、ガッツ石松法は公約数の個数を求める場合にも使えます。

でもね、再三申し上げますが理屈を理解してから使ってくださいよ。とくに予習シリーズを使っている小学4年生はまだ場合の数を習っていません。

理解させるのは困難を極めます。まるで東京オリンピック。

また、連除法は2つの数の約数を求めるときに使いますが、1つの数の素因数分解にも使えます。ま、これは連除法とは言わないですけどね。

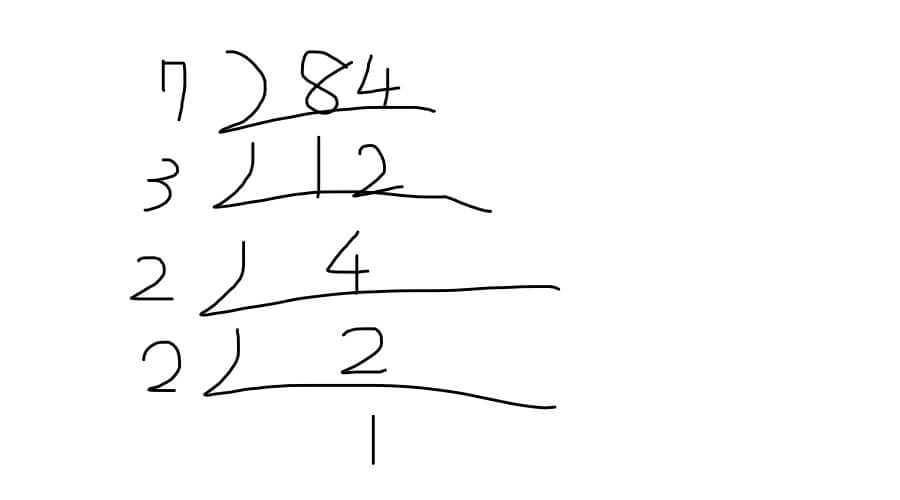
試しに84を素因数分解しました。

1×2×2×3×7

となりましたね。

ここでも約数の個数を求めるときは場合分けします。

・かけ算をしないパターン　1、2、3、7

・2個のかけ算をするパターン　2×2、2×3、2×7、3×7

・3個のかけ算をするパターン　2×2×3、2×2×7、2×3×7

・4個のかけ算をするパターン　2×2×3×7

全部のパターンを数えると12です。

なお、約数の個数を求める場合は左側の割る数字だけではなく、下の数字も含めて数えていきましょう。1をお忘れなく。

さて、念のため84の約数を力技であげていきましょう。

1、2、3、4、6、7、12、14、21、28、42、84

はい、12個ありましたね。

数の話で終始した今回。

まさか約数の説明でガッツ石松先生が出てくるとは私も思いませんでした。竹原慎二先生もアップしておられます。

これが独自性、すなわち多様性。

ウィーアーザワールド。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介