【中学受験】差集め算の解き方　線分図を書きましょう

もう夏期講習も終わりましたよね。

小学4年生のお子さんがいらっしゃる日本津々浦々のご家庭から

「はぁ〜、ようやく夏期講習が終わる・・・。宿題の山ももう少しで終わる。もう少しの辛抱！」

という勇ましいお言葉が漏れ聞こえるようであります。

YT-NET加盟の塾では夏休みに入ったと思いきやいきなり「夏期講習だ！夏を制する者は受験を制す！」と謎の掛け声とともに連日にわたる『夏期講習』と銘打った集金イベントの始まりが告げられます。夏期講習テキストが配布されたかと思いきや、宿題がやたらと出され、何日も連続で塾に行くはめになり、果ては普段とは別の先生がたどたどしい授業を展開して子どもたちを苦しめるのであります。

そんな夏期講習、そして夏休みも終わりです。

夏休み初めの頃の「この夏は弱点を補強して、余裕を持って二学期を迎えるのだ！」という初心はいきなりぶっ放される宿題の山と、消化不良の単元にまみれて8月も半ばをすぎた頃には息も絶え絶え。

「はぁ、ようやく終わる・・・」

と、嘆息とともに終わるのであります。日本中そこかしこで見られる中学受験夏休みあるあるであります。

小学4年生の、とくに算数は差集め算、方陣算、ならべ方、組み合わせなどこの短期間で学習するには消化不良になりそうな単元を学習したかと思われます。

まぁ、普通に考えて詰め込みすぎですよ。分からなくて困るのが当然です。

今回はささやかながら差集め算を亀甲縛りにしていきたいと思いますよ。ささやかな亀甲縛りがどんなものかは想像にお任せいたします。ソフトタッチでいきます。オラオラ。

差集め算は3パターンしかない

いきなり大きく出ました。

差集め算には3つのパターンしかありません。

すなわち、

1.不足と不足のパターン

2.あまりとあまりのパターン

3.不足とあまりのパターン

です。

アレンジを加えるとややこしい問題でも基本的にはこの3つのパターンを覚えて応用すれば対応できます。少なくとも4年生ではこの3パターンを押さえておけば十分です。

例題をちゃんと読みましたか？読んでない？

読みましょうよ。例題に全て載ってます。

ただ、予習シリーズでは大切なことが書いてないんですよね。

それは、差集め算を解く時は必ず線分図を書くということです。

どうしてテキストの中で『線分図を必ず書け』と指示していないのか不思議でたまりません。和差算みたいな感じで線分図を書くのがキモです。

え？線分図が書けない？それ、問題解くよりも線分図を書く練習をした方がいいですよ。

和差算も、差集め算も線分図を書く練習のような単元です。

上に挙げたような3つのパターンも線分図さえ書けりゃ余裕でございます。

「そもそも線分図が書けないんだけど？」

いいですね、練習しましょう。基本問題やら練習問題やら色々ありますが、問題解くより線分図を書く練習をしましょう。

差集め算の線分図には下の4つのパターンしかありません。

1.不足

2.あまり

3.部分的に不足

4.分配

それぞれ書き方を説明していきます。

1.線分図の書き方のコツ　〜不足のパターン〜

問い

「子どもたち全員に7個ずつりんごを配ろうとすると15個足りません」

線分図

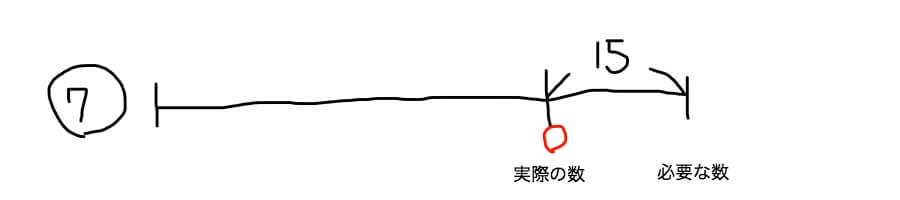
不足の線分図の書き方のコツは、

1.左横に配る個数を丸で囲んで書いておく

→上の問題だったら「7」ですね。これはどのパターンの線分図でも共通です。

2.実線で「必要な数」まで線を引く

→線分図の右端です。

3.実際の数のところに線を引く

→「必要な数」から左に縦線を引いて、実際の数と「必要な数」の間に15と書き込んでおきます。

4.実際の数のところに丸印をつける

→赤丸の部分です。

このように線分図を書くと何個ずつ配るのかが分かりやすくなりますし、丸印をつけておくことで必要な数と実際の数を混同しなくなります。何より視覚的に分かるってのがミソです。

この通りじゃなくてもいいんですが、自分なりに書き方のルールを決めておいた方が絶対にいいです。

2.線分図の書き方のコツ　〜あまりのパターン〜

次はあまりのパターンです。

問い

「子どもたち全員に3個ずつりんごを配ると5個あまります」

線分図

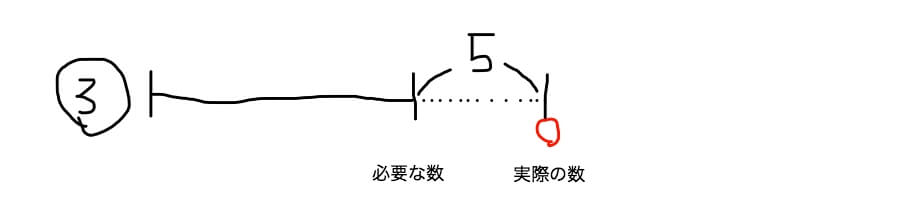
あまりの線分図の書き方のコツは、

1.左横に配る個数を丸で囲んで書いておく

→上の問題だったら「3」です。

2.実線で「必要な数」まで線を引く

3.実際の数のところまで点線を引く

→「必要な数」から右に点線を引いて縦線を書きます。あまりの数である5を書き込んでおきます。

4.実際の数のところに丸印をつける

→赤丸の部分です。

あまりが出る場合の線分図はあまりの部分を点線で書きましょう。

必要な数までは実線で必ず書く、と決めておくといいですね。

3.線分図の書き方のコツ　〜部分的に不足のパターン〜

これはちょいとややこしいですが、要領は同じです。ではやっていきます。

問い

「子どもたち全員に8個ずつりんごを配ると1人には4個しか配れず、残りの2人には配ることができません」

線分図

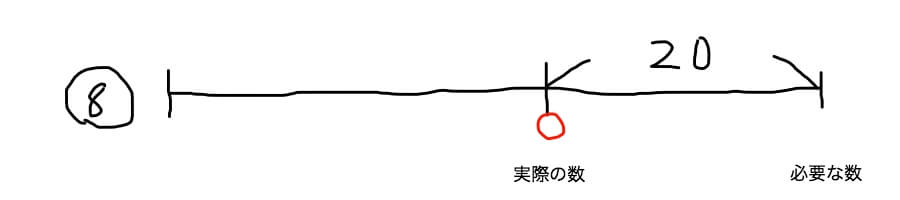
部分的に不足の線分図の書き方のコツは、

1.左横に配る個数を丸で囲んで書いておく

→上の問題だったら「8」とします。部分的に不足（あまる）するパターンの場合は配る数を一つに決めちゃってください。

2.実線で「必要な数」まで線を引く

→線分図の右端です。

3.実際の数のところに線を引く

→部分的に不足がある場合は、問題文中に足りない数がはっきり書いてありません。

この場合ですと、1人に4個しか配れなかったので、8ー4＝4個足りず、2人には1個も配れなかったので8×2＝16個足りません。したがって8個ずつ配るとすると20個足りないことになります。

4.実際の数のところに丸印をつける

→赤丸の部分です。

部分的にあまりが出る場合も不足の場合と同じで、配る数をそろえてあまりを計算すればいいです。

4.線分図の書き方のコツ　〜分配するパターン〜

問い

「りんごを2人には6個、1人には5個、残りの子どもたちには1個ずつ配ったところあまりが1個となりました」

線分図

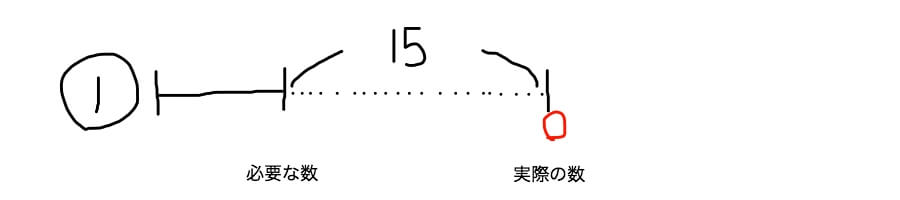
これはちょいと難しいかもしれませんね。

分配するパターンの線分図の書き方のコツは、

1.左横に配る個数を丸で囲んで書いておく

→上の問題だったら「1」です。「なんで1やねん！」と突っ込まれそうですが、この場合も基本的には分配する数は一つに決めちゃうんです。

ただ、「6」とか「5」ですと不足やあまりを計算できません。「1」ずつ配ったと仮定すると、あまりを求めることができます。なのでここでは「1」ずつ配ったと決めちゃうんですよ。

あまりの求め方は下に書いてます。

2.実線で「必要な数」まで線を引く

3.実際の数のところに点線を引く

→「1」ずつ配ったと仮定すると、2人には6個ずつ配るわけですから、2×6ー1×2＝10個あまることになります。

同じように1人には5個配るわけですから5ー1＝4個あまります。

もともと余っている1個も含めて「1」ずつ配るときの全体のあまりの数を計算すると、10＋4＋1＝15個あまることになります。

なので点線部分は15個となるわけです。

4.実際の数のところに丸印をつける

→赤丸の部分です。

線分図を書く意味

「差集め算なんか線分図書かなくたって解けるじゃん！」

なーんて意見をおっしゃる方は、なぜ4年生のこの段階で差集め算を勉強するのかが分かっていらっしゃらない。

差集め算といういわゆる特殊算の解き方を通して本当に学ぶべきは、文章を図式化して整理するスキルです。

図式化して整理するスキルは小学5年生、6年生になるとめちゃくちゃ使うようになります。

例えば今後学習する割合とか速さとかいったような中学受験において、とっっっても重要な単元でも使いますよ。

その時に、図式化できませーん！差集め算の解き方しか知りませーん！とかいうんじゃお話にならないわけです。

そもそも本番の入試で差集め算もろバレの問題なんかほとんど出てきません。結果的に差集め算の考え方を使うとしても、その過程の考え方、図式化、整理の仕方が問われるわけでして、

「ヤッホー！差集め算の解き方覚えた！」

とか小学4年生の段階でウキウキしてても図式化や整理といった本質的な力が身についていないと苦労すること請け合いでございます。

なのでとにかく書け、線分図を書け、と申し上げたい！ってか申し上げてるけど。

差集め算、３つのパターンの解き方

線分図を書くことに比べれば差集め算の解き方なんぞ屁みたいなもんです。

３パターン一気にいきます。

1.不足・不足のパターン

問い

「子どもたちにりんごを7個ずつ配ると15個たりません。5個ずつ配ると5個たりません。子どもの人数とりんごの人数を答えなさい」

線分図

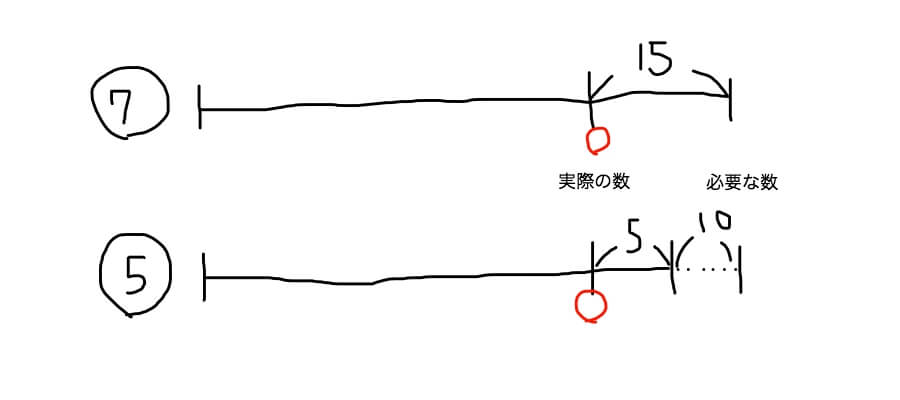
解き方

（15ー5）÷（7ー5）＝5・・・子どもたちの人数

一人に7個配るのと、5個配るのとだと2個の差が出ます。一人当たり2個ずつ差が出るわけですね。

7個ずつ配る時と5個ずつ配る時とでは、全体で10個の差が出ますよね。微妙に線の長さがおかしい線分図で表した通りです。

全体の10個の差を一人あたりの差である2個で割ると、子どもの人数が出ます。

5×7ー15＝20・・・りんごの個数

子どもの人数が分かったのであとは7個ずつ配った場合に当てはめるとりんごの個数が出ます。

答え　5人、20個

2.あまり・あまりのパターン

問い

「子どもたちにりんごを3個ずつ配ると5個あまります。2個ずつ配ると10個あまります。子どもの人数とりんごの人数を答えなさい」

線分図

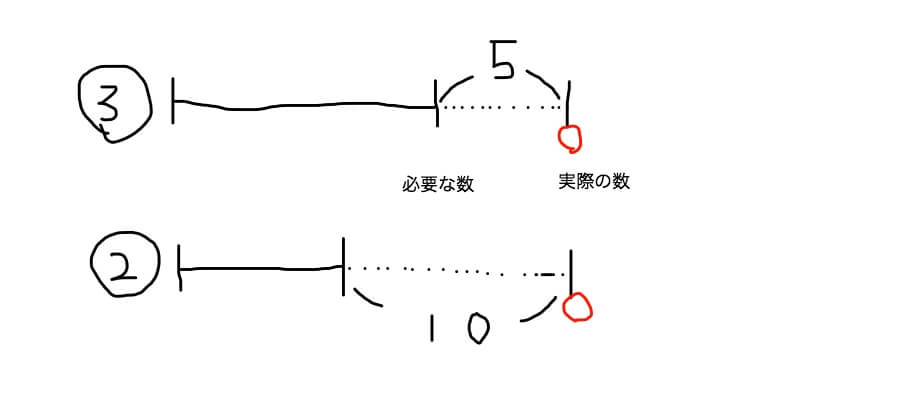
解き方

（10ー5）÷（3ー2）＝5・・・子どもたちの人数

これも考え方は不足・不足の場合と同じです。一人に3個配る場合と、2個配る場合とでは一人当たり1個ずつ差が出るんです。

3個ずつ配る時と2個ずつ配る時とでは、全体で5個の差が出ますよね。

全体の5個の差を一人あたりの差である1個で割ると、子どもの人数が出ます。

5×3＋5＝20・・・りんごの個数

子どもの人数が分かったのであとは5個ずつ配った場合に当てはめるとりんごの個数が出ます。

答え　5人、20個

3.不足・あまりのパターン

問い

「子どもたちにりんごを8個ずつ配ると20個たりません。3個ずつ配ると5個あまります。子どもの人数とりんごの人数を答えなさい」

線分図

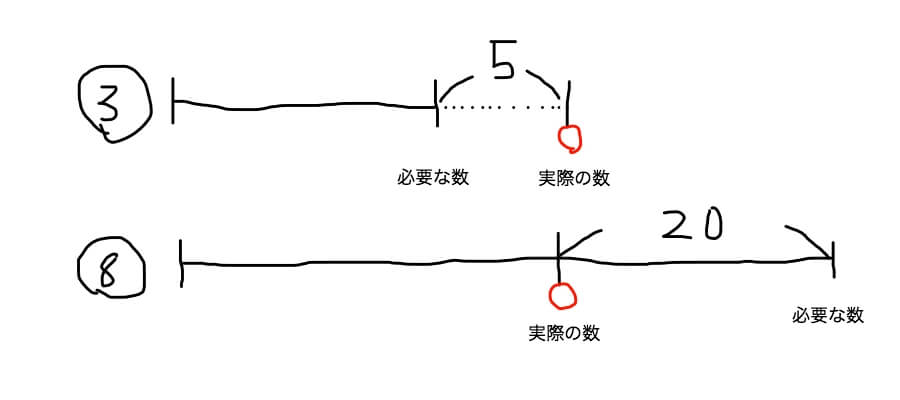
解き方

（20＋5）÷（8ー3）＝5・・・子どもたちの人数

線分図を見ればわかるように、8個ずつ配る時と3個ずつ配る時とで25個の差が出ます。

一人あたりの差は8ー3で5個ですから、25÷5で5人と出てきます。

8×5ー20＝20・・・りんごの個数

子どもの人数が分かったのであとは8個ずつ配った場合に当てはめるとりんごの個数が出ます。

答え　5人、20個

差集め算のまとめ

小学4年生レベルの差集め算ですと3パターンの解き方を覚えれば十分対応できます。

が、しつこいようですが線分図だけは書けるようにしておいてくださいね。

4パターンの線分図を書けるかどうかがキモです。難しく見える問題もあるかもしれませんが、4パターンの線分図のどれなのかが分かって書くことができれば解けるようになってます。

ちゃんとした塾の先生でしたら線分図のありがたさを耳にタコができるくらい説法してくれるはずです。

中学受験の算数ではいろんな特殊算がありますが、本当に大事なのは特殊算の解き方そのものではなく、解く過程の考え方、整理の仕方です。

予習シリーズにもうっすら書いてありますが、お子さんが本当に大事なことをそこから読み取るのは不可能です。

ぜひ、親御さんがきっちり読み取って伝授してあげてくださいな。

少しだけ尊敬されるかもしれません。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介