【中学受験】小学4年生予習シリーズ算数　第8回「三角形の角」をマスターする

大学受験改革をはじめとして思考力養成やらなにやら巷間かまびすしく、知識詰込み型の弊害が叫ばれるうららかな春、みなさんどうお過ごしでございましょうか？

「とにかく宿題大変！こんなにやることあるなんて思わなかった・・・！これじゃまるでわたしたちが塾の尻拭いしてるみたい！」

と嘆きつつもやることリストを整理して一日のスケジュールを作成し、ぐうたら息子・娘に怒鳴り散らす日々に辟易としておられるのではないでしょうか。

あぁ、それは正常な姿です。どこのご家庭も一緒でございます。

とりわけ中学受験を経験したことのないご家庭での喧騒はひとしおです。

解説を読んで意味もわからないままなんとなく説明してみたり、果ては精神論「やればできる！」の陥穽にはまってにっちもさっちもいきません。

私が最も大事だと思うことの一つは教材研究でございます。つまり、自分で教材を読み込んで問題を解き、咀嚼し、質問されたらどう答えるかに備える営みです。

あ、いきなり解説はしないほうがいいですよ。

子供って解説とかあんまり聞いてないですからいきなり解説しても意味がございません。

分からない、解きたい気持ちになる頃を見計らって「どれどれ」としゃしゃり出て行くのが作法です。

さて、ご自分でも意味が分からないことを説明すると聞かされる方はさらに意味が分かりません。

意味不明の無限ダンジョンです。

そこで、とくに親御さんが聞かれて困る算数を中心に毎週なんとなく説明していこうかと考えております。

もちろん使用テキストは予習シリーズ。

で、今日は多分このへんをやってるんじゃないかなー、という推測で「第8回　三角形の角」を親御さん向けに説明していきます。

なんか昔の四谷大塚みたいですね。日曜教室に付き添いにきた私の母も授業受けてましたねぇ。

三角形の角における前提となる知識

どんな学習単元においても問題に解答するための前提となる知識がございます。

予習シリーズ第8回「三角形の角」の問題を解答するためには以下の知識が前提となります。

・三角形の3つの角の和は180度

・二つの辺の長さが等しい三角形を二等辺三角形と呼ぶ

・二等辺三角形の3つの角のうち、2つの角の角度は同じ

・三つの辺の長さが等しい三角形を正三角形と呼ぶ

・正三角形の角の角度は全て60度

・三角定規には直角三角形と直角二等辺三角形の２種類がある

・三角定規の直角三角形のそれぞれの角の角度は30度、60度、90度

・三角定規の直角二等辺三角形のそれぞれの角の角度は45度、45度、90度

・複合図形は二等辺三角形、正三角形、直角三角形、直角二等辺三角形を発見すると解けるようになっている

これがこの回の肝です。そして基本です。すべて解説に書いてありますし、例題では実例を交えて解説してくれております。

基本が大事と言い続けた理由はここにあります。私が基本おじさんとバカにされても歩みを止めないのは、上の前提知識＝基本事項が分かっていれば解けるようになるからです。

逆に基本知識が身についていないと解けません。

だったら例題と類題を使って知識を覚えて、使えるようになりましょうや、というごくごく当たり前の提言をし続けているにすぎません。

そもそも、思考をするには知識が必要です。知識は詰め込むのが早道です。

思考力や解答力の前提には正しい知識の習得があります。

それがないのに思考力なんか身につくわけありません。

なのでまずは正しい知識を習得しよう、とささやいているのでございます。

では三角形の角を攻略するため具体例にいきましょう

三つの問題を出します。

すべて答えられますか？

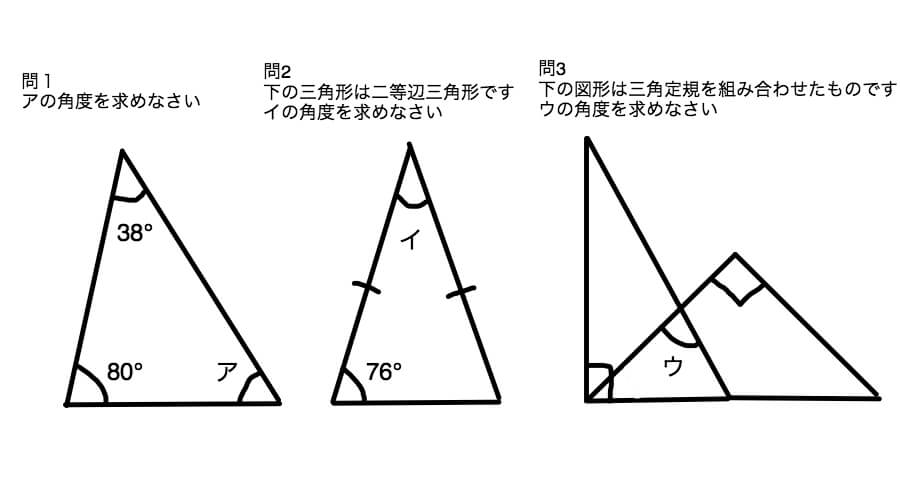
この問題はすべて基本知識が頭に入っていればすぐさま解ける問題です。

これが基本です。

フリーハンドで書いてますので線がヨレていますし、角度も正確ではございませんがまぁ許してください。

では順番に解答していきましょう。

問１の解答

問1の三角形の角度は38°、80°という二つが分かっていて、後の一つ「ア」が分かりません。

が、「三角形の三つの角の和は180°」という知識があれば、

180-(38+80)=62

答え　62°

と求められます。

問2の解答

問2で分かっている角度は76°の一つのみです。

が、「二等辺三角形の二つの角の角度は等しくなる」基本知識を活用しますと向かい側の角の角度は76°と分かります。

したがいまして、イの角度は

180-(76+76)=28°

答え　28°

と求められます。

問3の解答

これは角度が一つも書いてありません。こんなん解けるかよぉ！と思いきや、問題文で「三角定規を組み合わせた」ものと書かれていますね。

つまり、三角定規は「直角三角形（30°、60°、90°）」と「直角二等辺三角形（45°、45°、90°）」の2種類ですから、図形の中に角度が書かれていなくても角度が分かるんです。

この基本知識を図形の中に書き込みますと下のようになります。

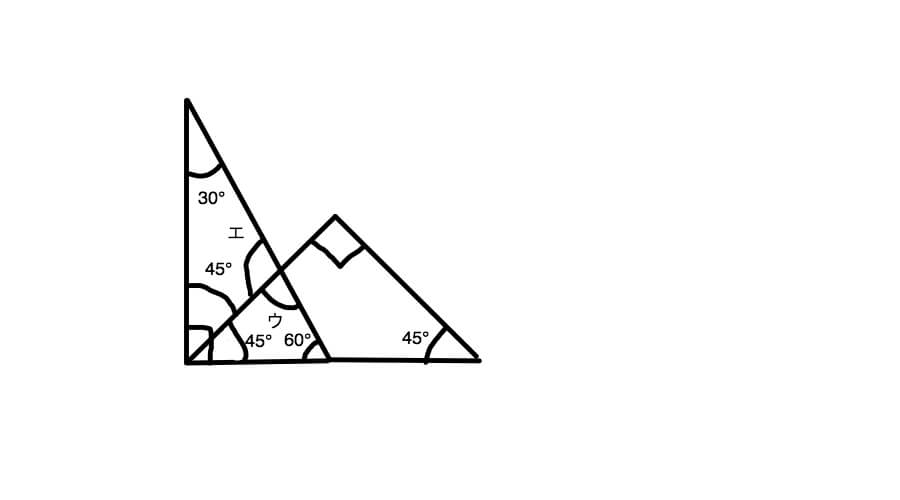
つまりウは三角定規の角度の知識と三角形の三つの角の和の知識の二つがあれば解答できます。

180-(45+60)=75

答え　75°

さらにエという角度も追加してみました。

「直線を半回転させたときの角度は180°」なのでエは180°からウの角度を引けば求められると分かります。

180-75=105

答え　105°

と求められます。

三角形の角の求め方、その奥義

上の問題、超簡単でしたよね。

なんで超簡単かって、基本的な知識のみで解ける問題だからです。

ところが、基本的な知識を組み合わせたり、隠されていたりすると途端に難易度が上がります。嘘みたいな話だと思いませんか？

思わない？いいでしょう。

一つ一つの基本的な知識で解ける問題は超簡単。ところがこれが組み合わさるとどうやって知識を利用すればいいのか途端に分からなくなるんです。

また、基本知識をそのまま当てはめられず、隠されていたりすると難易度が上がります。

組み合わせたり、隠れた基本事項を発見するスキルがあれば「あぁ、あれとこれとそれを組み合わせれば解けるねー」と余裕シャクシャクで正解をぶっ放せますが、基本的知識に落としこめるように整理するスキルを持たないと何がどう組み合わさっていて、どう解くべきかが皆目見当つかない事態に陥ります。

このスキルこそが思考力ってやつだと言われております。

が、思考力派の人たちに残念なお知らせがございます。

変な訓練をしなくてもパターン認識で思考力系の問題は解けるようになってます。

予習シリーズ第8回「三角形の角」の問題はどんなに複雑に見えても二等辺三角形や正三角形、そして三角定規の直角三角形、直角二等辺三角形のかたちに落とし込んで整理すれば解けるんですよ。

そのための奥義言っちゃいますよ。

複雑に見える問題は角度を求める前に同じ長さの辺を整理する、これに尽きます。

ではちょっと難しい問題を出します。

ちょっと難しい問題がやってきたヤァヤァヤァ

チャゲ&飛鳥じゃないですよ。ビートルズです。

まあいいです、下の問題を解いてください。

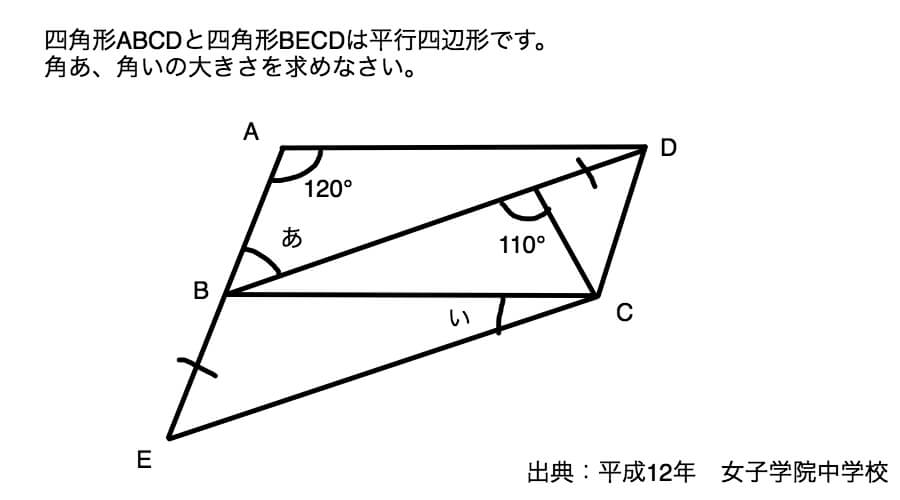
急に「おや？」と思いませんでした？

これ、ただの基本的知識の組み合わせで解ける問題なんです。

簡単だと思う人はこれ以降読み飛ばしていただいて大丈夫ですよ。

ではアムロいきまーす。

一見するとよくわからないので同じ長さの辺を探していきましょう。

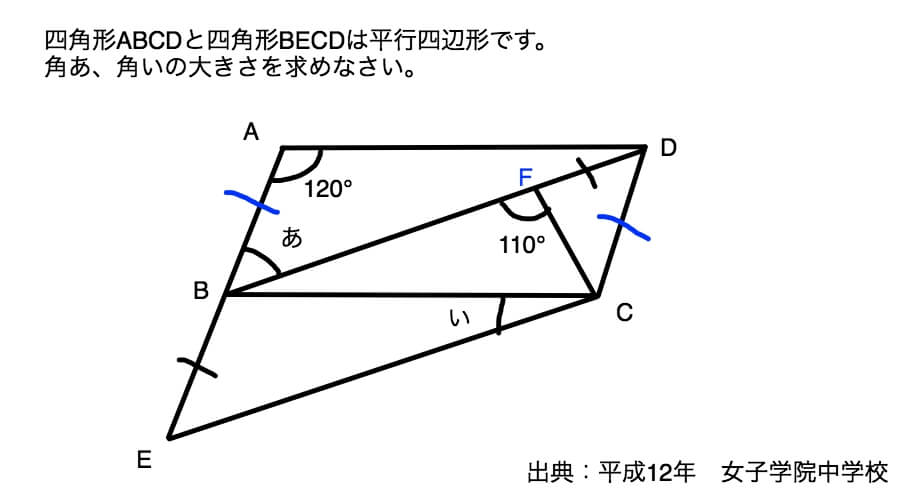
青で一本線を引いた辺が同じ長さで、かつ黒の一本線で引いた辺も同じ長さです。

なぜかっていうと、四角形ABCDは平行四辺形なので、辺ABと辺DCは同じ長さになります。

そして四角形BECDも平行四辺形なので、辺BEと辺CDも同じ長さです。

ついでに点Fも追加しておきました。

同じ長さの辺を見つけたら何が見えました？

二等辺三角形が出現しましたね。

三角形FDCの二辺が同じ長さです。二等辺三角形の出現でございます。

なので、角DFCと角DCFは同じ角度です。

二等辺三角形の長さが同じ辺の両側の角の角度は同じだって予習シリーズに書いてますもんね。

そして角DFCは180-110で70°と求められます。ということは角DCFも70°です。

角FDCが求められそうですね。そう、180-(70+70)=40°です。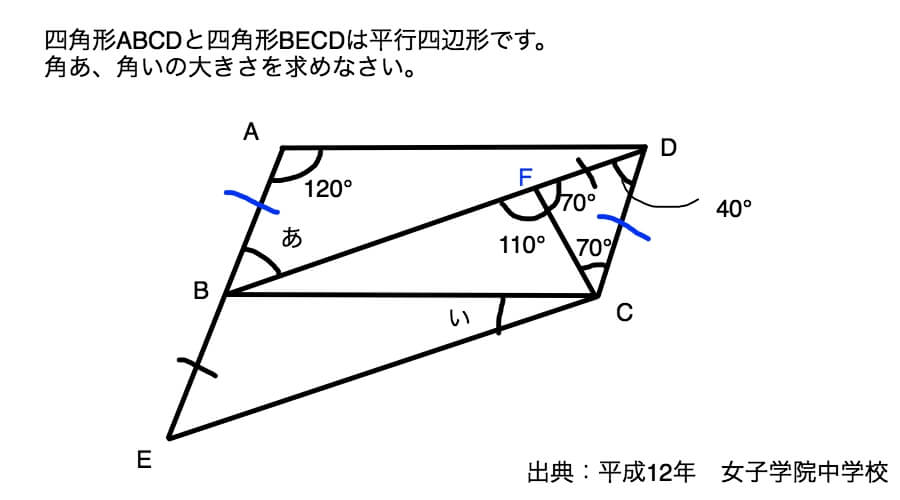

ところで、角FDCと角ABDは錯角の関係にあり、辺ADと辺BCは平行なので角FDC＝角ABDです。

というわけで「あ」は40°。

次に「い」を求めます。

「あ」が求められれば順番に角度を求めていけば出てくるんですけど、せっかくなのでこれまでやった知識を活用していこうと思いますよ。

角BADと角EBCは同位角です。辺ADと辺BCは平行なので角BADと角EBCの角度は等しくなります。

したがいまして角EBCは120°です。

さらに角ABDと角BECも同位角です。辺BDと辺ECは平行なので角ABDと角BECの角度は等しくなります。

したがいまして角BECは40°です。

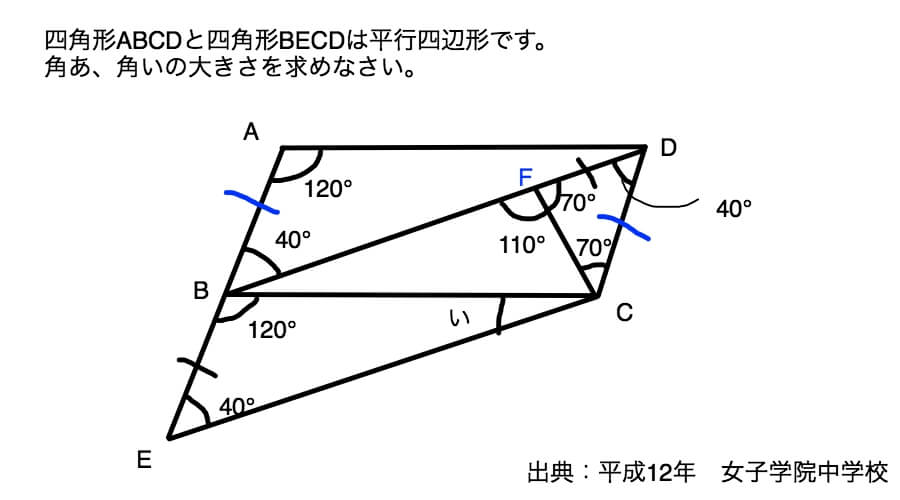
三角形の三つの角の角度の和は180°ですから角BCE（い）は180-(120+40)=20°となります。

答え　あ40°　い20°

基本知識が通用する段階まで問題を解きほぐす

上で出したちょっと難しい問題でございますが、同じ長さの辺を見つけて二等辺三角形を見つけてからは余裕じゃなかったですか？

基本的な知識だけで解けましたよね。

私が使った知識は↓だけです。

・二等辺三角形は二辺の長さが同じ三角形である

・長さの同じ二辺の両側の角度は同じである

・二辺が平行であるときの同位角の角度は同じになる

・二辺が平行であるときの錯角の角度は同じになる

・三角形の角度の和は180°になる

では初見で「おや？」と思われた方、なんで「おや？」と思われたと思います？

それは、基本的知識で解けるレベルまで問題が解きほぐされていないからです。

仮に三角形FDCが最初から二等辺三角形であることが分かっていたなら、引っかかりは軽減されたはずです。

ちょっと難しい問題や応用問題は基本的知識で解けるんですが、それがうまい具合に隠されているんです。

私はこれを隠れた前提条件と呼んでいたりします。

隠れた前提条件、どうやって見つけたか覚えていますか？

そうです、最初に同じ長さの辺を見つけていきましたよね。

今回の予習シリーズ第8回「三角形の角」においては、隠れた条件を探し出すためのコツは「同じ長さの辺」を見つけることであり、それがダメなら「同じ大きさの角」を見つけることです。

中学受験の算数の問題はどんなに難しく見えても、基本知識と隠れた前提条件を見つけ出すテクニックを身につけていれば大抵は解けます。

こういったテクニックは塾の先生がよくご存知ですので、いっぱい質問していっぱいテクニックを盗んでくるといいと思いますよ。

算数ができる子の正体

算数ができる子たちの頭の中では、こういった思考が躍動しております。

そんな偏差値70キッズたちも2通りに分類されます。

一つは本当にめちゃくちゃ頭のいい子。こういう子は少ないですが、一定数います。

でもそういう子は目指すべき対象ではございません。

だって再現性がないんですもの。

二つ目は難しい問題を解きほぐすためのテクニックをたくさん身につけている子。

難しい問題を解きほぐして簡単な問題に変換するコツを知っているボーイズアンドガールズ。

普通のお子さんをお持ちの親御さんが目指すべきはこういう子たちです。

なぜなら再現性があるから。つまり、極端に言えば誰でも到達できるから。

私が申し上げた解きほぐすスキル。これが普通の子が上を目指すために身につけるべきスキルです。

このスキルは練習によって身につきますが、間違った練習をしていると時間ばかりが経過してしまいます。

なので、「角度を求める時は同じ長さの辺（もしくは同じ大きさの角度）に注目するといいよ」というマジックワードを炸裂させて欲しいんです。

マジックワードを炸裂させるタイミングは、練習問題の後半とか応用問題を解いていて悩んでいる時です。

もう、ダメだと諦め、どうやったら解けるんだろう、どうしたらいいんだろう、悩んだ挙句「ちょっといい？」と聞いてきた瞬間。

少し時間を置いて、おもむろに、

「あぁ、こういう問題はね、角度じゃなくて同じ長さの辺を見つけて、二等辺三角形を見つけるといいよ。例えば、こことことは同じ長さでしょ。じゃあ、これは二等辺三角形だよね。ここは？」

私の経験上、この時に

「アーッ！」

ってなります。

こういうのアハ体験って言うんですか？それとも野獣先輩？

まぁ、アハ体験でも野獣先輩でもどちらでもいいんですが、最終的に自分の力で解けた実感を残して終わると自信につながります。

そのためには待つ。とにかく待つ。一撃必殺を繰り出す瞬間を待って待って、ここぞというタイミングでかめはめ波なのであります。

いきなり解説なんかしちゃダメですよ。

小学4年生は人の話なんか大して聞きませんからね。

でも弱り果てて困り狂った瞬間の一撃は効きます。

翌日からいきなり「お母さん！（お父さん！）」の一言がワンオクターブ高くなるかもしれません。

ってわけでご自分が教材研究をした成果を喋りたくて喋りたくてケツからすごいモノが出そうな時も待つのが肝要です。

待つことを覚えた結果、怒り狂っていたママが観音菩薩に見え、臭かったパパがファブリーズの香りに包まれているかのような反応に変化いたします。

最後に。

学習において最も大事なのってなんだと思います？

信頼関係です。

アディオス。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介