【中学受験】四谷大塚予習シリーズを使用した予習の仕方　小学4年生算数

「予習の仕方なんかわかんねーよ」とお嘆きの紳士淑女の皆様、今日も送迎ご苦労様でございました。

なに？一人で電車で通っているから大丈夫ですって？

この前、総武線の秋葉原で一目散に座席に座りたそうなおばあさんを出し抜いた四谷大塚の4人組見ましたよ。その4人、おばあさんそっちのけでゲームに興じておりました。

電車を使わせるならまずは優しさを身につけさせた方が良いと思う次第でございます。

さて、以前に予習はいいぞ、と言いました。

【中学受験】塾の予習と復習　目的と方法を押さえると学習効果は倍増する

予習のメリットは、

1.授業を受ける目的が明確になる

2.学習内容を圧縮できる

3.再現性がある

という3つです。

今回は予習の仕方を四谷大塚の予習シリーズ、小学4年生の算数を使いながらやっていきたいと思います。

予習シリーズ算数4年（上）第4回和差算

さて、新小学4年生、つまり小学3年生の2月下旬から3月初旬にやるのが算数の和差算です。

第1回〜第3回までは計算の基礎と角度です。第4回で初めて「〜算」ってやつが出てきます。今日はこいつをしばいていきたいと思います。

1　和と差の線分図

さて、和差算です。こいつを使って予習の仕方をやっていきましょう。

写真を撮る腕もだいぶ上がってまいりました。

上の写真を見ていただくとちょうど真ん中より下あたりに、こう書いてますね。

数量の大きさを直線の長さで表し、数量の大小の関係を考えやすくした図のことを線分図といいます。線分図で、数量の和や差は次のように表現します。

引用元：予習シリーズ算数4年（上）第4回「和差算」より

ここで予習して覚えておきたいのは数ってのは線分図を書くと関係が分かりやすくなったりするんだぜ、って点です。

下に必修例題１なるものがあります。見えない？私の写真技術を恨むといいでしょう。

で、その必修例題１も解く。でも、解けるかどうかは大した問題ではありません。

あくまで大事なのは「数ってのは線分図を書くと関係が分かりやすくなったりするんだぜ」という考え方の理解です。

2　和差算（2量）

次のページではこれ。

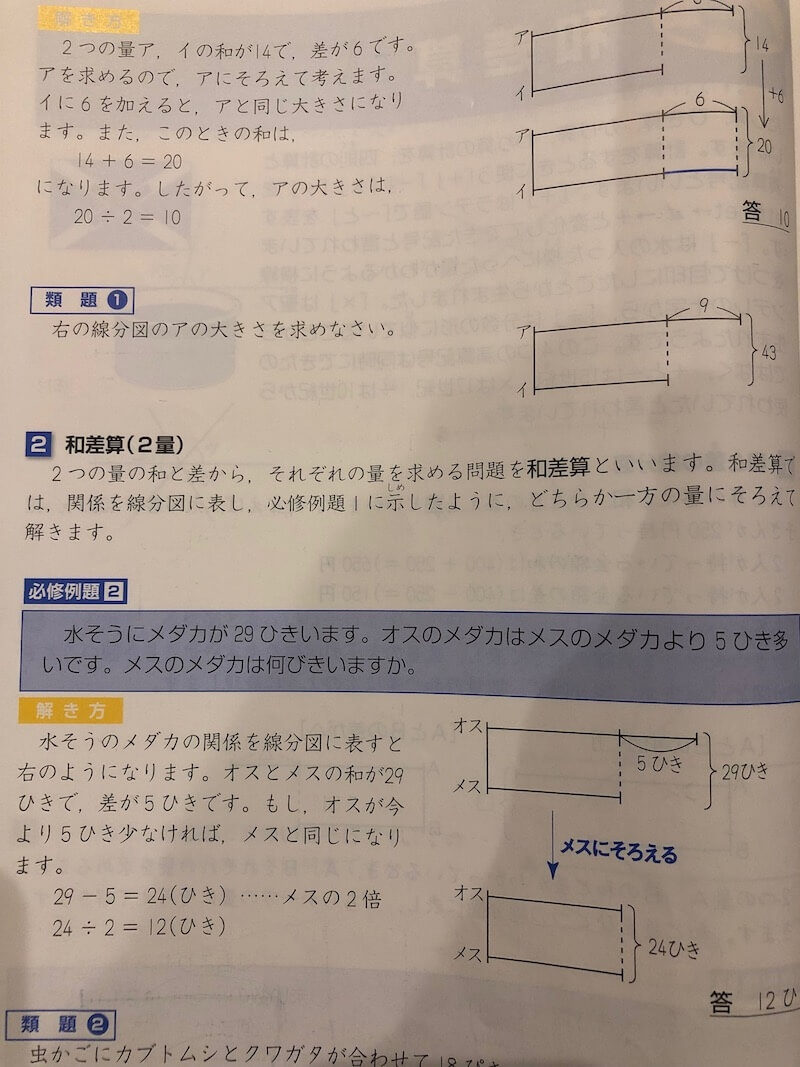
ここでは和差算について説明し、「関係を線分図に表し、一方の量にそろえて」解くんだよ、と言ってますね。

そうすると必修例題2が解けるってわけですが、それよりもここでちゃんと理解しておきたいのは「数字同士の関係は線分図に表すと分かりやすくなるんだぜ」という考え方です。

3　和差算（3量）

さあ、和差算の最後です。

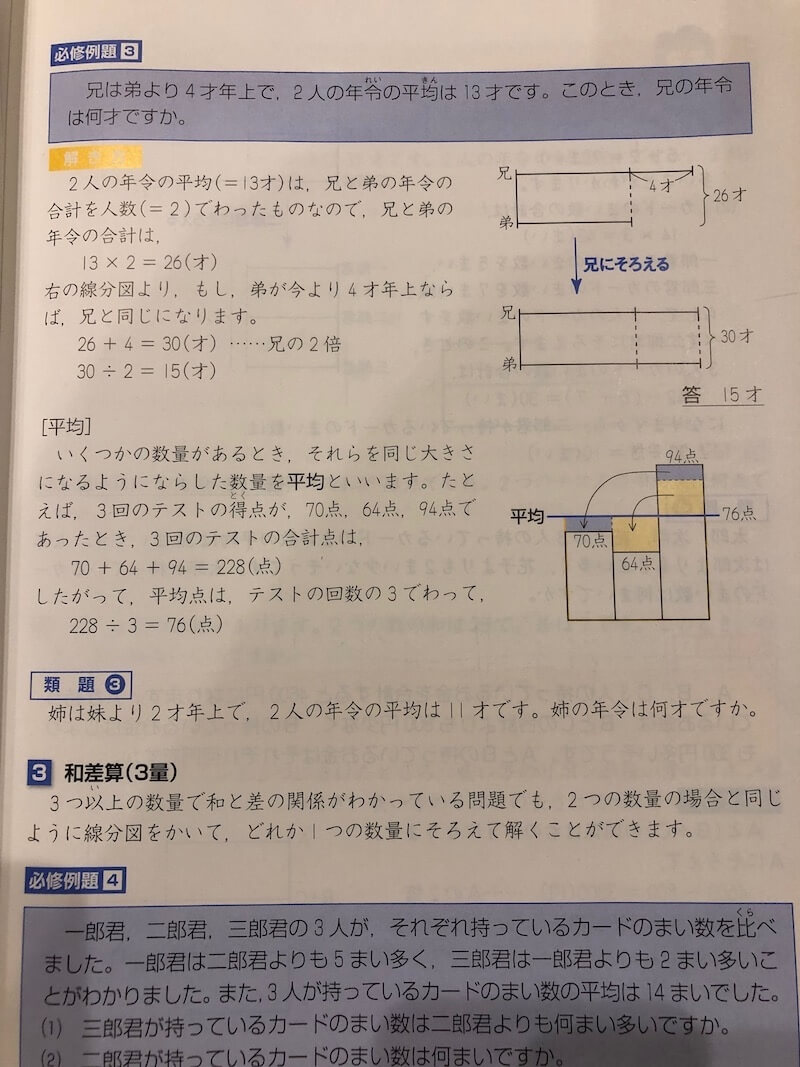
さっきは2つの関係性でしたが、今度は関係性が3つになりました。

でも心配ご無用。

「2つの数量の場合と同じように線分図をかいて、どれか一つの数量にそろえて解くことができます。」ってわけ。

上のようなことを理解すると、必修例題は解けます。でも何度も言いますが、必修問題を解けたからいいというわけではございません。

算数で大切なのは解き方ではなく考え方

私、3回も「必修例題を解けるかどうか」は大事じゃない、と言いましたね。

正確に言いますと、解けたという結果ではなく、解くに至った過程での考え方が大事なんです。

ブッブー！→「解き方を覚えたゾ！線分図を書いて一番少ないのに揃えるんだな！」

ピンポーン！→「数字という目に見えないものを、線分図という目に見えるものに置き換えると考えやすくなるゾ！」

ブッブー！の方は「和差算」の解き方を身につけました。

ピンポーン！の方は数字を具体的な形（線分図）に整理して解く方法を「和差算」で身につけました。

これ、えらい違いですよ。

一方は基本的な和差算しか解けません。

一方は数字を具体的な形（線分図）に変換して分かりやすくする方法を学んだんです。

ではこの2つの違いがどのような形で現れるのか見てみましょう。

和差算の問題を解く

和差算の基本問題

姉と妹の持っているお金の平均は1300円です。姉が妹より400円多く持っているとすると、妹の持っているお金は何円ですか。

引用元：予習シリーズ算数4年（上）第4回「和差算」より

これを線分図にしてみましょう。

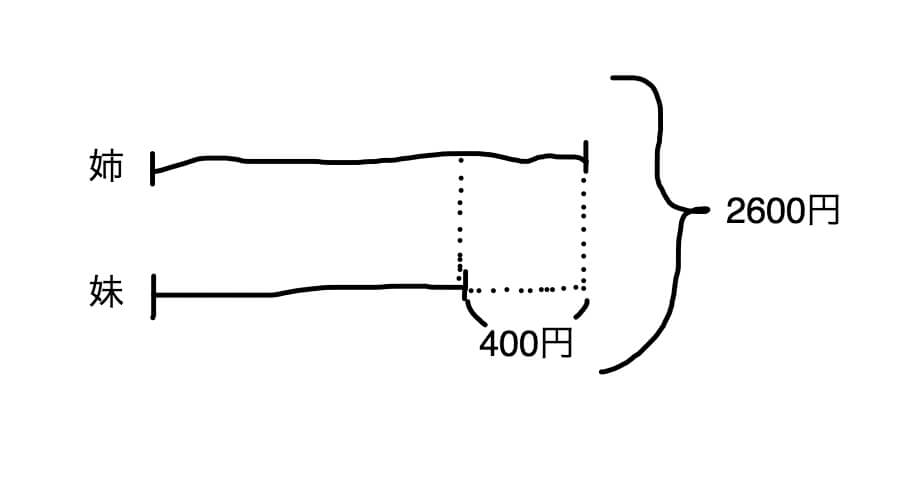
解答は（2600ー400）÷2＝1100円です。

ここまでは単純に和差算の解き方と平均の考え方を当てはめるだけで解けます。ブッブー！の人も解けそうです。

では、ほんの少しだけ難しい練習問題を解いてみましょう。

春子さんと秋子さんの持っているお金を合計すると840円になります。もし、春子さんが秋子さんに180円あげると、2人の持っているお金は等しくなるそうです。これについて次の問いに答えなさい。

（１）春子さんは秋子さんよりも何円多く持っていますか。

（２）春子さんの持っているお金は何円ですか。

引用元：予習シリーズ算数4年（上）第4回「和差算」より

この問題が少しだけ難しいのは「あげると」という点です。

基本事項として学んできた和差算における差そのものではなくて、差を埋めるための数量になっているんです。

出てきた数字を単純に和差算的に線分図にする、と覚えた子供は180円が差だと思うかもしれません。でも、本当は差は360円です。

「あげる」という行為を線分図で表現するとどうなるかを理解して、表現する必要があるわけですね。

つまり、問題文で与えられた条件を整理してそれを線分図という思考の道具に落とし込めないと間違えます。

数字という抽象を線分図というツールに落とし込み、条件を整理して、解ける形に変形する。

これが和差算でやっていることです。

予習シリーズを使った予習の仕方

さて、小学3年生の子供が一人で予習をしていて、

「ふむ、和差算は線分図というツールを使って問題文で与えられた数字を具体形に変換して整理し解を導く一つの方法だ」

と思い至りますでしょうか？

ま、普通は思い至りませんよ。

せいぜい、線分図の書き方を覚えて、数字を当てはめる方法を覚えるくらいが関の山です。

でもそれでいいんです。

それだけでも基本問題全部と練習問題（標準問題）の半分くらいは解けますから。

大事なのは解けなかった問題です。

なぜ解けなかったのか。

条件が複雑で線分図に整理しきれなかったから？線分図を使って問題を整理する方法に慣れていないから？

素晴らしい。授業を受ける目的ができました。

線分図を使って問題を整理する方法を学びにいけばいいんです。授業を受ける目的ができたじゃないですか。

これが予習です。

予習でどこまで何をやるか

当然のことながら、説明はちゃんと読んで覚えてくださいよ。

そして、基本問題と練習問題（標準問題）は解きましょう。全部解けちゃった？じゃあ、演習問題集を全部解いちゃいましょう。解けなかった問題があるのであれば、解けなかった理由を特定しておきましょう。

で、その解けなかった理由を潰しに授業に行ったらいいです。

ちなみに小学6年生の予習シリーズでも和差算の問題は復習として出てきます。

小学4年生のテキストよりちょいと難しくなってますよ。

でも問題で与えられた条件を線分図に変換する方法を覚えた子だったら楽勝。和差算を覚えただけの子は解けない。

算数は解き方を暗記するのも大事ですが、根本的な考え方を理解し覚えないと使えるようになりません。

小学6年生の必修例題はこんな感じです。随分様相が変わってますよね。

「5個の連続した奇数の和が135であるとき、5個の中でもっとも小さい数はいくつですか。」ですって。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介