【中学受験】中学入試頻出の計算の工夫　実践問題演習を解きながら覚える

計算の工夫の基本は分解して共通する数を見つけてその数でくくる、です。

ってか、それだけです。

共通する数を「共通因数」なんてかっこよく言ったりしますが、あんまり難しい言葉は使いたくないものです。

数学の用語は中二病っぽいのと、はたからは何言ってるのか分からないのが特徴です。

進学校のまわりでは

「おれは今、収束して極限になったのだ・・・！」

とか、わけの分からないことを言っている男子がたまにいますが、要約すると「振られた」のであります。

ちゃんと誰でも分かるように言ってほしいですよね。

さて、「分解して共通の数を見つけてくくる」だけではわけが分かりません。

どうやるのかが大事です。

説明するより実例を見て頂いた方がくっきりしっぽり理解できるのかと思い、5題ほど例題を用意いたしました。

↓これ

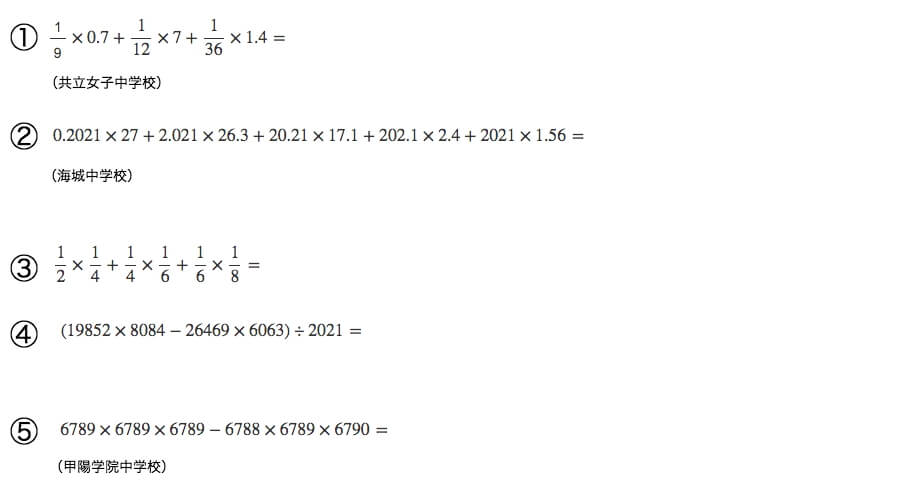
なんかやべぇ数字が力強く並んでます。

力技でやります？

めっちゃやりたくねぇよ、ママン！

計算の工夫なんぞ前前前世に置いてきちゃったよって方はそろそろ目を覚ますといいかもしれません。

青いカプセルを飲むか赤いカプセルを飲むかはお任せいたします。

赤いカプセルを選ぶ方はこの不思議な世界の続きが見られると思いますよ。

本日説明する計算の工夫

あぁ、ローレンス・フィッシュバーン先輩にそそのかされて赤いカプセルを飲んでしまったのですね。

いいでしょう。

どうでもいいんスけど、ローレンス・フィッシュバーン先輩といえば「地獄の黙示録」ですよね。

先輩が演じていたやせっぽっちのアメリカ兵と、マトリックスの堂々たる体躯との雲泥の差にひっくり返りましたよ。

人類共通の感想であります。

いきなり例題を解く前に本日ご説明する計算の工夫を技能別に挙げておきます。

①共通な数（共通因数）の発見

計算式のすべての項で同じ数をかけているとき、そいつを共通因数と言ったりします。

たとえば、

3×5+7×5

は3×5と7×5の2つの項で5をかけていますから、5が共通な数（共通因数）になります。

こいつの発見がキモです。

②共通な数（共通因数）への変形

これも例を出します。

3×5＋7×10

ってな計算があったとします。こいつを共通な数（共通因数）を持つように変形すると、

3×5＋7×2×5

となります。

更に変形すると

3×5＋14×5

となり、共通な数（共通因数）が出現いたします。

ついてきてますか？ほら、教室の隅っこにいるからと言って寝ないでくださいよ。

③分配法則

正式名称は分配法則。私は「くくる」と言ってます。

タイガーマスクと佐山聡みたいなものです。

どっちも一緒。

ああだこうだ言うより見てもらった方が理解しやすいと思いますから①、②の式を分配法則を使います。

①3×5＋7×5

②3×5＋14×5

を分配法則を使ってくくります。

①(3＋7)×5=50

②(3+14)×5=85

上のように共通な数（共通因数）が見つかると「くくれる」んですよ。

これ、大事。

④小数を分数に直す

小数を分数に直すのは計算の工夫ってよりはただの基本動作です。

暗記しとくといいでしょう。分母が8になる小数は暗記マストです。

0.125=1/8

0.25=1/4

0.375=3/8

0.625=5/8

0.75=3/4

0.875=7/8

⑤部分分数分解

「ぶぶんぶんすうぶんかい」と読みます。

ターミネーター2の「ダダンダンダンダダン」のリズムで読むといいです。

これも理屈はいいので例をあげて説明します。

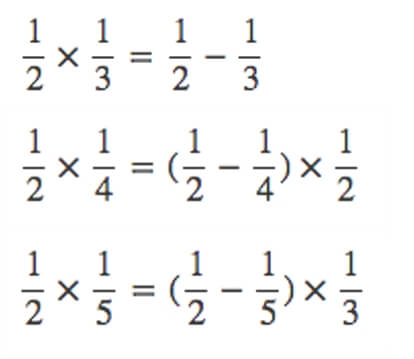
分数同士の掛け算をこんなふうに直せるんです。

これを「ぶんぶんぶん」といいます。

間違えました、部分分数分解です。

どうしてこうなるのかは小学校の学習指導要領から外れますから割愛します。高校数学です。

⑥面積図

面積図も使いますよ。

たとえばですね、

200×204ー199×205

とかいう絶対に計算したくないやつがいるとするじゃないですか。

こういうときに面積図を使います。

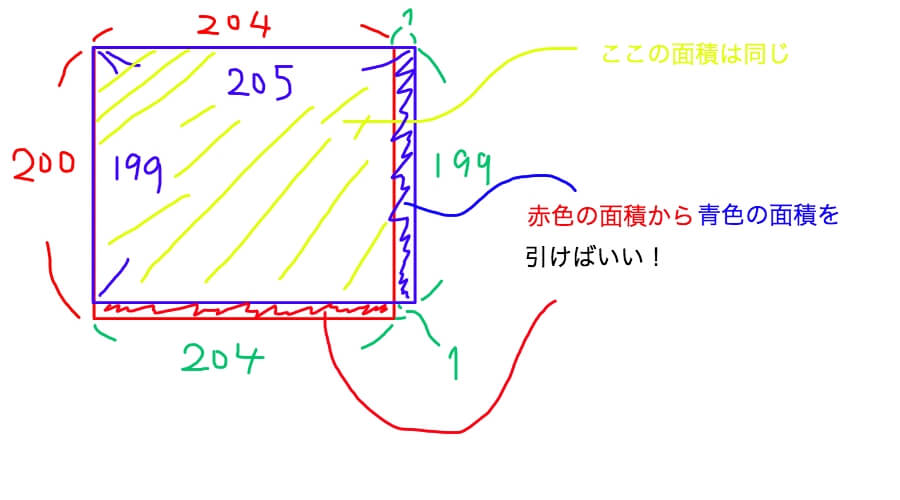
面積図を書いたつもりがただのガチャガチャした絵を描いてしまいました。

要するに、

200×204ー199×205

をオラついて計算しなくても、面積図を使うと

204×1ー199×1

で求められると言いたいんです。いえ、言わせていただきますよ。

例題①　分解して共通する数を見つける

①の共立女子中学校の問題を解いていきましょう。

ではもう一度①の問題を見てみましょう。

なんか力技でいけるようないけないような微妙なところをついてきますよね。

オラオラしてもいいんですが、ここはスマートにいきましょう。

この式を↓のように直してみましょう。

小数、分数の混合が出てきたらとりあえず分数に揃えるのは基本中の基本です。

おやおや怪しげなやつが一匹いますね。

お前だ！

この怪しいやつの郎党もチラチラ見えています。

分母が同じやつらです。3匹います。

ただ、分子が違います。

そこでこいつらを同じ分子にしちゃいます。

すると、こうなります。

共通の数である7/10が出現しましたね。

共通の数を引っ張り出したら、もうこっちのものです。

くくりましょう。

・・・と、その前に「×10」と「×2」が邪魔ですね。

もうね、どっかに掛けちゃいましょうよ。掛けて退散してもらいましょう。

するとこうなります。

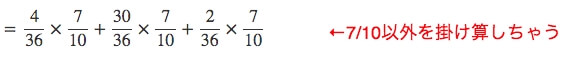
きれいに7/10で揃いましたね。

じゃあ、もうやることは一つ。

あらためてくくります。御免！

くくる作業はみなさんが大好きな分配法則ってやつを使います。

カッコの中を計算すると↓のようになります。

答えはもうおわかりですよね。

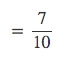
はい、7/10と求められました。

ちなみに数式は以下の数式入力便利ページで入力しました。サンキュー外人。

HostMath

一連の流れは下の通りです。

計算の工夫　例題①の振り返り

まずは共通の数（共通因数）になりそうなやつを見つけます。

例題①ですと7/10です。

全部、7/10がだったらいいんですがそうもいきません。

そこで7/10になるように分解します。

分解して共通の数が出てきましたら、分配法則を使ってくくれる形に直します。

そしてくくる、と。

基本的にはこれだけです。

では次の問題にいってみましょう例題②です。

1 2 3 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介