開成中学入試問題「算数」を徹底解説、平成28年度大問３（３）場合の数ー第17回

開成中学の入試問題らしく気づきと論理で解く良問

前回、前々回で言っていますがこの問題、私は大好きです。開成中学が算数の問題を解くにおいて求めていることを凝縮したような問題だと思います。

解いたことのないような問題を、習ったことを基礎として、何らかの事実に気づき、論理で解く、というのが開成中学の算数の問題に多いように見受けられます。この問題もしかり。もしかしたらSAPIX近辺では超優秀な教師あたりがこんな問題を出題してトレーニングしているのかもしれませんが。

とはいえ、開成中学の先生がたはとても優しく大問３のメインディッシュともいえる（３）を解くために必要なことを（１）、（２）で問題として出題し、受験生に解かせることでヒントを提供しています。

難しい問題を解くためのヒントを問題として出題するという傾向も開成中学では見られますね。やはり、多少手心を加えているのでしょう。

さて、それでは解いていきましょう。

step1　条件を整理する

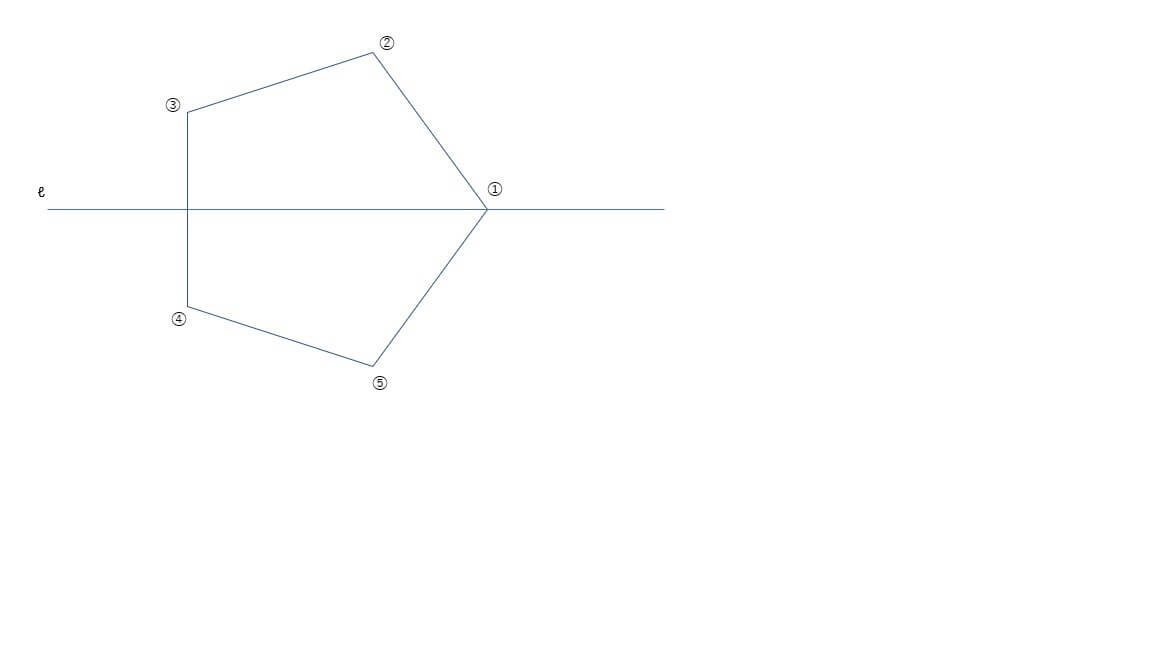
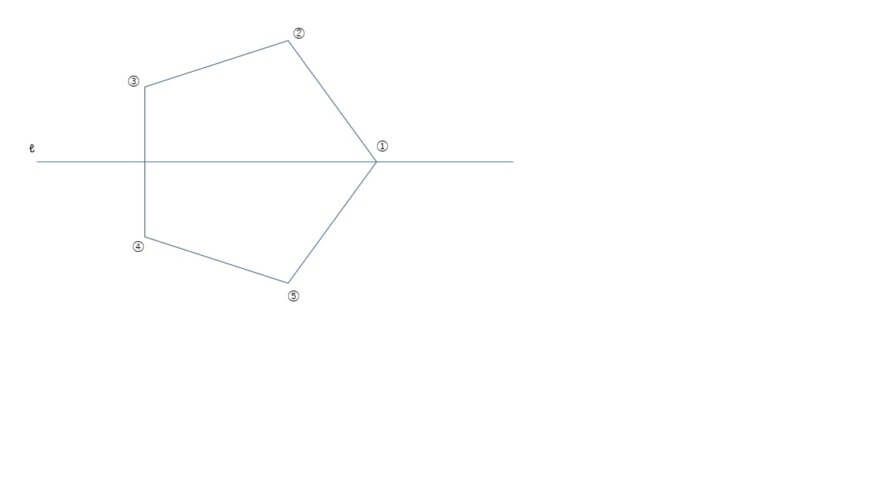
図の正五角形は直線ℓに関して線対称です。いま、点Aが正五角形の頂点①、②、③、④、⑤を、操作１、操作２、操作３のいずれかに従い移動します。

操作１：時計回りに２つ移動する

操作２：時計回りの反対の方向に1つ移動する

操作３：直線ℓに関して線対称な頂点に移動する

たとえば②からスタートして、操作１、操作２、操作３、操作３、操作１の5回の操作による点Aの移動は、次の例のように表記します。操作３、操作２、操作３、操作３、操作１による移動も同じ表記になります。

例：②　⑤　①　①　①　④

以下の問いに答えなさい（答えのみでよい）。

（３）点Aが②からスタートして5回の操作の直後に④にいる移動の表記は全部で何通りありますか。さらに、その表記を上の例にならってすべて書き上げなさい。

問題文から提供されている条件は以下の通りです。

操作１：時計回りに２つ移動する

操作２：時計回りの反対の方向に1つ移動する

操作３：直線ℓに関して線対称な頂点に移動する

・操作手順ではなく頂点の移動経路を問う。

step2　隠れた条件を発見する

（１）、（２）の問題を解くことによって得られる答えは隠れた条件です。

すなわち、

（１）の解答によって得られる条件：②を出発した点Aが2回の操作によっていることができる頂点

前々回の大問３の（１）の解説で以下のようなパターンを書き出しました。

１、１　・・・　②、⑤、③

１、２　・・・　②、⑤、①

１、３　・・・　②、⑤、②

２、１　・・・　②、③、①

２、２　・・・　②、③、④

２、３　・・・　②、③、④

３、１　・・・　②、⑤、③

３、２　・・・　②、⑤、①

３、３　・・・　②、⑤、②

この問題で求められているのは操作のパターンではなく、移動のパターンです。

上記より重複した移動のパターンを除くと、②を出発した点Aが2回の操作により移動するパターンは以下の5つです。

②⑤③

②⑤①

②⑤②

②③①

②③④

（２）の解答によって得られる条件：1回の操作で点Aが④にいられるような頂点

前回の大問３の（２）の解説で以下のように求めました。

①と③が1回の操作で点Aが④にいられるような頂点である。

step3　解答の方向性を決める

関連性に気づく

ここまでで明示された条件と隠れた条件を挙げていきました。

そして、以下の問題と（１）、（２）に関連性があることに気づくと方向性が定まります。

（３）点Aが②からスタートして5回の操作の直後に④にいる移動の表記は全部で何通りありますか。さらに、その表記を上の例にならってすべて書き上げなさい。

なんと、（３）の問題で問われている「最後に④がいる」ためにはその直前の操作の直後には、（２）で明らかにされた隠れた条件より、①か③にいないといけないではないですか！

つまり、表記としては、「②→＊1→＊2→＊3→①か③→④」になるのです。

そしてそして、（１）で明らかにされた隠れた条件から、②をスタートしたあとの＊1と＊2のパターンはすでに求められているではないですか！

すなわち、こうなります。

②⑤③

②⑤①

②⑤②

②③①

②③④

ということは上記の2回の操作による移動地点のパターン「③、①、②、④」から、「①か③に移動するパターン」を求めれば、5回の操作によって④に到達するパターンが割り出せるのです。

どうしてそんなことに気づける？

こういうことに気づけば解けるよ、と言うのは易し行うは難し。

「（３）の問題を解くのには（１）と（２）の問題の解答が役に立ちそうだな。どれどれ、見てみよう。ほらやはりだ」

などと普通は考えつくわけがありません。でもね、簡単に気づく方法があるんですよ。

それは、開成中学の算数は前の問題をヒントとして次の問題が解けることが多い、という知識をもってすると気づけるんです。

これめちゃくちゃ大事ですよ。開成中学に受かりたかったらこの傾向は絶対に知識として抑えておいてください。

この知識をもとにして私が解いたときの思考を辿ると、

なんだこれ5回も操作があるのか。やけに前の問題との難易度に差があるな。

↓

5回の操作が時計回り方向に「操作１：＋２」と「操作２：ー１」みたいな定型的な形だったらパターンの算出で求められるが、操作３は＋２も＋１も０－１もー２もあり得る。膨大な操作パターンを洗い出して移動の表記に変換するのには時間がかかりすぎる。

↓

これ多分、別のやり方がある。どうせ前の問題を条件にするんだろ。

↓

ほら、（２）は④に至る前の移動地点のパターンを求めてる。この問題の最終地点は④だ。共通してる。条件として使えそうだ。前の操作は①か③になる。

↓

（１）は②からスタートした2回の操作のパターンを求めてる。この問題も②からスタートしてる。偶然のわけがない。操作の始まりと終わりでの移動地点の表記をヒントにして、その間を求めりゃ正解に導ける、そういうことだろ？

↓

開成中学の教師の良心を信じるッ！

気づきと論理性

「（１）と（２）の問題で求めた解が隠れた条件として使える」

これが気づきです。

「（１）の解は操作の始まりからのパターンを明らかにしている。（２）の解は最後の操作の一つ前のパターンを明らかにしている。ということはその間のパターンを求めれば（３）の解は得られる」

これが論理的思考です。

step4　解答の道筋を決める

（１）の解の最終地点のパターン、つまり2回目の操作の直後の移動地点のパターンは「③、①、②、④」です。

（２）の解の最終地点のパターン、つまり、4回目の操作の直後の移動地点のパターンは「①、③」です。

つまり、２回目の操作直後の「③、①、②、④」から4回目の操作直後の「①、③」に移動できる操作３の移動地点を求めれば良いのです。

これを場合の数として列挙します。

③→＊3→①

③→＊3→③

①→＊3→①

①→＊3→③

②→＊3→①

②→＊3→③

④→＊3→①

④→＊3→③

さあこの＊３を検討していけば解答を得られます。もう少しです。頑張りましょう。

step5　計算する

③→＊3→①を満たす＊３

〇1　3回目の操作１により①に移動し、4回目の操作で操作３を行うことにより①に移動可能です。

×　3回目の操作２では④に移動してしまい、①には移動できません。

×　3回目の操作３では④に移動してしまい、①には移動できません。

③→＊3→③を満たす＊３

×　3回目の操作１では①に移動してしまい、③には移動できません。

〇2　3回目の操作２により④に移動し、4回目の操作で操作３を行うことにより③に移動可能です。

〇3　3回目の操作３により④に移動し、4回目の操作で操作３を行うことにより③に移動可能です。

①→＊3→③を満たす＊３

〇4　3回目の操作１により④に移動し、4回目の操作で操作３を行うことにより③に移動可能です。

〇5　3回目の操作２により②に移動し、4回目の操作で操作２を行うことにより③に移動可能です。

×　3回目の操作３では①に移動してしまい、③には移動できません。

①→＊3→①を満たす＊３

×　3回目の操作１では④にしてしまい、①には移動できません。

×　3回目の操作２では②に移動してしまい、①には移動できません。

〇6　3回目の操作３により①に移動し、4回目の操作で操作３を行うことにより①に移動可能です。

②→＊3→①を満たす＊３

〇7　3回目の操作１により⑤に移動し、4回目の操作で操作２を行うことにより①に移動可能です。

〇8　3回目の操作２により③に移動し、4回目の操作で操作１を行うことにより①に移動可能です。

〇9　3回目の操作３により⑤に移動し、4回目の操作で操作２を行うことにより①に移動可能です。

②→＊3→③を満たす＊３

〇10　3回目の操作１により⑤に移動し、4回目の操作で操作１を行うことにより③に移動可能です。

×　3回目の操作２では③に移動してしまい、③には移動できません。

〇11　3回目の操作３により⑤に移動し、4回目の操作で操作１を行うことにより①に移動可能です。

④→＊3→①を満たす＊３

×　3回目の操作１では②に移動してしまい、①には移動できません。

〇12　3回目の操作２により⑤に移動し、4回目の操作で操作２を行うことにより①に移動可能です。

〇13　3回目の操作３により③に移動し、4回目の操作で操作１を行うことにより①に移動可能です。

④→＊3→③を満たす＊３

〇14　3回目の操作１により②に移動し、4回目の操作で操作２を行うことにより③に移動可能です。

〇15　3回目の操作２により⑤に移動し、4回目の操作で操作１を行うことにより③に移動可能です。

×　3回目の操作３では③に移動してしまい、③には移動できません。

〇をつけた可能な操作パターンの移動地点パターンを列挙する

〇は15個あります。

「わーい、操作２までのパターンは４通りだから、４×１５＝６０だー」と解答してしまうあなたは頭が良いけどおっちょこちょい。

「ふふふ、重複を抜けば良いのだろう。〇２と〇３は重複している。〇７と〇９と〇１１も重複している。だから答えは重複している分の３つを除き１２だ！」と解答してしまうあなたは条件を忘れがち。

えとね、（１）で求めた条件はこうなってるんですよ。

②⑤③

②⑤①

②⑤②

②③①

②③④

step5で求めたパターンは以下の通り。

操作2直後に③がくる場合の操作3のパターンは2通り

操作2直後に①がくる場合の操作3のパターンは3通り

操作2直後に②がくる場合の操作3のパターンは3通り

操作2直後に④がくる場合の操作3のパターンは4通り

この問題、移動地点のパターンを求めてるんです。操作2直後の移動パターンは以下の通りです。

②⑤③

②⑤①

②⑤②

②③①

②③④

したがって、操作3直後の移動パターンは以下のようになります。

②⑤③　2通り

②⑤①　3通り

②⑤②　3通り

②③①　3通り

②③④　4通り

２＋３＋３＋３＋４で答えは15通り。

移動の表記はこうなります。これが表記パターンの答えです。

②⑤③④③④

②⑤③①①④

②⑤①①①④

②⑤①④③④

②⑤①②③④

②⑤②⑤①④

②⑤②③①④

②⑤②⑤③④

②③①①①④

②③①④③④

②③①②③④

②③④⑤③④

②③④⑤①④

②③④②③④

②③④③①④

これ、ちなみに親御様解けます？

この問題を解くには、開成中学が大問中の前の問題を手掛かりにして今の問題を解けるのが多いという知識を前提に、前の問題の解答が合っていて、前の問題を解くことで得られた解答を論理的に読み解いて解答の道筋を作り、道筋に沿ってパターンを洗い出し、問題文で問われていることを把握しつつ５つの操作による移動経路のパターンを列挙する、ことが必要です。

普通の親御様では解けませんよ。しかもこれを小学生に解かせるんですよ。普通の小学生だったら解けるわけないに決まってるじゃないですか。

だからこそ、親御様が開成中学の問題を分析して傾向を子供に教えることと、子供に論理的な読解を身に着けさせる必要があるんです。

私のブログではそんなことできるわけねえ！という親御様に向けて、解答のロジックを明らかにし、そのロジックを子供に教えて頂くことと、ロジックを身に着け再現性をもって解くための方法及び学習方法を子供に身につけさせてあげるためにやってます。

解説を身に着けさせたところで仕方ありません。解説の根底をなすロジックと、そのロジックを学習するため勉強方法や知識をお子さんに伝えてもらうのが重要です。

あるいはこんな問題は解けないと決め込んで「解けそうにない問題は抜かしなさい」と教えることも一計ではございます。

ちなみに私は親からそう言われました。

そうすると何が起きるか。

難しそうな問題は抜く習慣ができる

のです。

それじゃ難関校は受かりませんよ。ちなみに私は落ちましたからね！

あわせて読みたい

最新のホカホカ記事

書いている人の紹介