開成中学入試問題「算数」を徹底解説、平成28年度大問1(2)比の問題ー第10回
stepを更に細分化します
step1が二つの処理ー条件を整理する、隠れた条件を発見するーが併存していたのでこれを二つに分けて、更にstepごとに一つの処理に集中できるように今回以降はやっていきたいと思います。
step1 条件を整理する
B君がYを出発してからMでA君に出会うまでに「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍ですか。
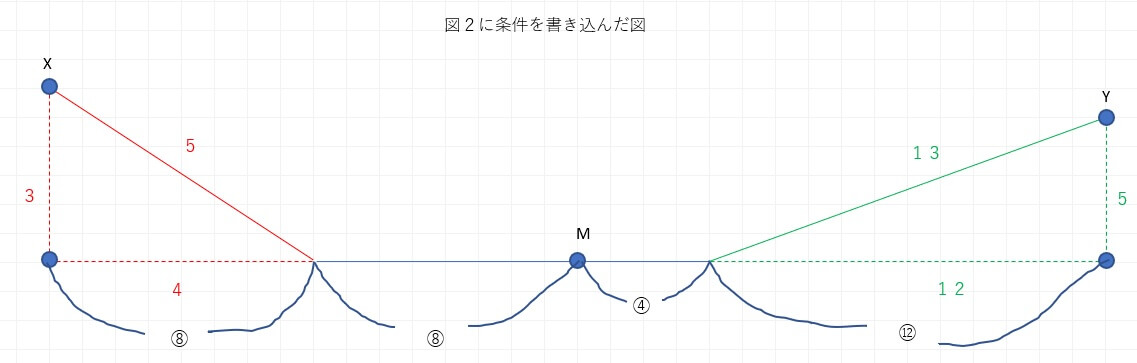
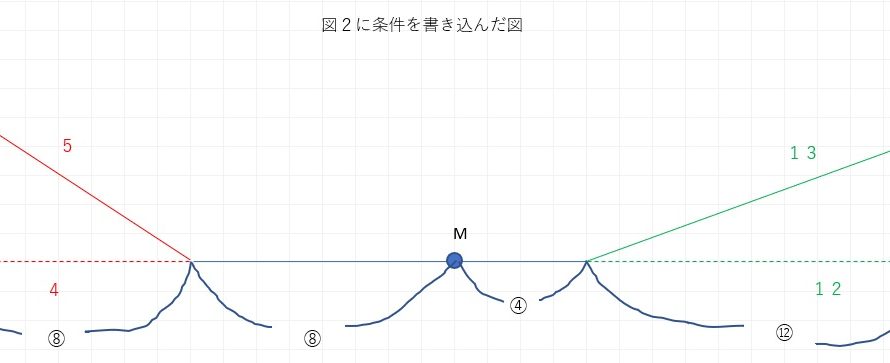
B君がYを出発したということなので、今度は5:12:13の直角三角形という目に見える条件を利用します。上の条件を整理した図の右側、緑色の三角形ですね。
また、直線距離で④+⑫でY地点からM地点まで直線距離だったら⑯となる、というのも目に見える条件です。
そして、B君はYを出発して下り坂を進んでいったので距離は⑬です。なぜなら⑫と下り坂の距離は12:13なので、この比から⑬という距離を導くことができます。
step2 隠れた条件を発見する
下り坂での速さの増加は「下向きに移動する長さ/横向きに移動する長さ×100」ですから、緑色の三角形の下向きの比=5を分子として、横向きの比=12を分母とした分数の分だけ速くなることになります。
つまり、5/12×100だけ速くなるということです。もともとの速さは1ですからこれの分母を12にすると、12/12と直すことができ、下り坂の速さは5/12+12/12で17/12となります。
ここまでが隠れた条件の発見です。
step3 解答の方向性を決める
この問題ではB君がYを出発してMにたどり着くまでの実際の時間(下り坂込み)が、想定の時間(下り坂を込まない)の何倍かという問題ですから、両者の時間を求めることによって何倍かが求められるものと考えます。
また時間を求めるのは、「距離÷速さ」ですから距離と速さが求められれば時間が求まります。
step4 解答の道筋を決める
ここでは、想定の時間における速さを1とおきます。そして距離は⑯です。
そして実際の速さは17/12です。ただし平坦な道は1の速さで進みます。距離は⑬+④で⑰です。
で、問題は実際にかかった時間は想定の時間の何倍かということですから、実際にかかった時間÷想定の時間で求められます。
ではこれを時間を求める式に落としてみましょう。
step5 計算する
ここでも数式を立てる段階と計算をする段階は同じタイミングで行うため、前回までのstep5とstep6は合体させてしまいます。以後の演習ではこのようにして解いていこうと思います。
想定の時間:⑯÷1=16
実際の時間:⑬÷17/12+④÷1=224/17
実際にかかった時間は想定の時間の何倍か、というのは式に表すと
224/17÷272/17=224/272
で、これを約分すると14/17となり、答えは14/17となります。
繰り返し言いますが、開成中学校の問題は正しく問題文を把握し、条件を整理して、かつ隠された条件を正しく発見して、基礎知識として頭に入れている処理方法を使用すれば必ず解けます。
それも繰り返し解答までの道筋をstepごとに分解していく学習をすれば、各stepにおける習熟度が高まり、正解に至る解答を十分な再現性をもって解くことが可能です。すなわち、どんな問題が出ても大丈夫な状態に必ずなるということです。
これもしつこく言いますが、何となく解けるのではいけません。練習によってstepごとの処理を正しく行うことでどんな問題でもとくことができる再現性を身に着けてこそ学習です。
そういった学習を常日頃から行うことができる子、もしくはこの理屈を教わらなくても身に着けている子、そういう子が本番の試験や未知の問題においても合格のための答案を再現性をもって作ることができ、合格することができるのだと考えています。
ですから合格するためにはこの解答ロジックを覚え、習熟することが極めて重要なのです。
あわせて読みたい
最新のホカホカ記事
最新のホカホカ記事の一覧はこちらから書いている人の紹介
星一徹のプロフィールはこちらから- 前の記事

開成中学入試問題「算数」を徹底解説、平成28年度大問1(1)①比の問題ー第9回 2018.06.27
- 次の記事

開成中学入試問題「算数」を徹底解説、平成28年度大問1(2)比の問題ー第11回 2018.07.04