開成中学入試問題「算数」を徹底解説、平成28年度大問１（２）比の問題ー第11回

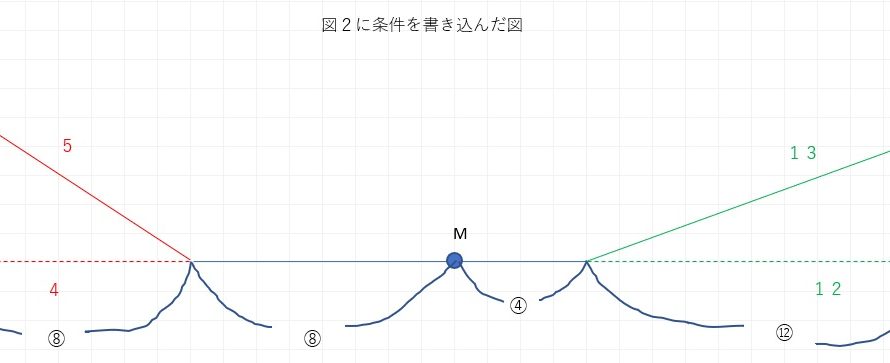
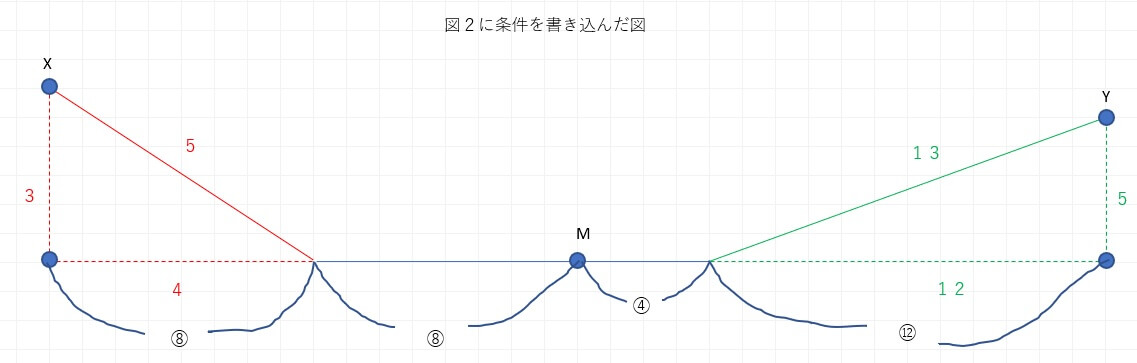
step1　条件を整理する

さて、いきなり問題文にいきましょう。

（２）A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」を求めなさい。

これを（１）でも使った条件を整理した図をもとに解きます。

次に、（１）の①、②でわかったことも明示された条件です。

すなわち、

①「A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」は「事前にB君が想定していた時間」の6/7である。

②「B君がYを出発してからMでA君に出会うまでに「実際にかかった時間」は「事前にB君が想定していた時間」の14/17である。

そして、問題文にあるように、

無事に、2人はちょうどMで出会いました。

ということで、下り坂があって進む速度と距離が変わって、Mにたどり着くまでの時間も変わったにも拘わらずちょうどMで出会ってます。

step2　隠れた条件を発見する

つまり、下り坂と距離が当初の想定から異なってMにたどり着くまでの時間が短くなったのにM地点でちょうど出会ったということは、A君とB君の想定より短くなった時間が同じであるということです。

これを文章によって式にすると、

A君がMにたどり着くまでの想定の時間の6/7＝B君がMにたどり着くまでの想定の時間の14/17

となります。

A君のもともとのM地点想定時間は⑦、実際の時間は⑥で差し引き①となります。

B君のもともとのM地点想定時間は（１７）、実際の時間は（１４）で差し引き（３）となります。

つまり、①＝（３）が成り立ちます。

step3　解答の方向性を決める

①＝（３）なので〇か（）のどちらかに変換してあげることで等式が成り立ちそうです。

step4　解答の道筋を決める

ここで最初のB君の想定を式にしてみます。

⑦＝（１７）＋15分

となります。step3で見たように、〇と（）をどちらかに揃えて解答を導くことができそうです。

では式を立て、計算をしてみましょう。

step5　計算する

⑦×３＝（１７）＋15分

で、これを計算すると、

（２１）＝（１７）+15分

ということは（４）＝15分ということが分かりますから、（１）の時間は15/4分です。

A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」を求めなさい。

というのが問題です。A君の実際にかかった時間は、（２１）×6/7＝（１８）です。

これを時間に直すと、（１８）×15/4＝６７．５分、つまり答えは1時間7分30秒となります。

とにかく条件の整理と隠れた条件を洗い出すこと、それも正確に

この問題も条件をきちんと整理して、隠れた条件を洗い出すことができればあとは流れ的に解くことができました。

逆に条件を整理せず、そこから隠れた条件も発見できない場合、この問題を解くのは難しいでしょう。

「どうしても解けない」「どこから手を付けていいか分からない」という悩みを抱いている人も、step1とstep2で明らかにした条件、隠れた条件を与えられれば「なーんだこういうことか」と解くことができるのではないでしょうか？

コツは解こうとしないことです。解くのではなく、「この問題で与えられている自明の条件は何かな？」そして「自明の条件をもとに隠れた条件を洗い出せるかな？」と考えてみてください。

開成中学校の問題でなくても構いません。応用問題が沢山掲載されている参考書を使って、step1とstep2をひたすら行ってみてもよいでしょう。実際に私もそうしました。

すると、条件の整理と隠れた条件の発見をする癖がつきます。この癖こそが未知の問題でも再現性をもって解く、ために身に着けたいことであり、それを身に着けることが学習なのです。

率直に言ってstep3～step5で気を付けるのは間違えた式を立てないことや、間違った計算をしないことです。これは条件の整理や発見に比べて容易に身に着けることができます。だから、受験まで半年以上あるのであれば、計算式を正しく立てることや計算の正確性を鍛えるよりも、条件の整理と発見に時間を割いてください。

計算は短期間で何とかなります。でも条件整理と発見は繰り返し繰り返し訓練しないと身につきません。

ただでさえ、塾歴が長い子はいきなり問題を解こうとする悪癖が身についているように思います。悪癖は長い時間をかけて直していかなければ直りません。

では今回の演習を終わります。おつかれさまでした。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介