開成中学入試問題「算数」を徹底解説、平成28年度大問３（１）場合の数ー第15回

未知の問題に対処する唯一の方法は基礎知識と論理的思考である

いきなりですが、この問題、私大好きです。

塾でこんな問題を解くことはないと思います。場合の数の解法を利用しますが、場合の数の理解だけでは到底解けません。未知の問題と言っても良いでしょう。

この問題を解くには問題文の正確な理解、前提条件の理解、そして解答を導くための論理的思考力が必要になります。

（１）、（２）は力業で誰でも解くことができますが、（３）を解けるということは基礎の知識に加えて圧倒的な論理的思考力がある、ということの証左であります。

開成中学校の求める生徒は、考えなく勉強ばかりしてきた生徒ではなく、論理的思考によって未知の事柄に対処することができる柔軟な生徒なんでしょうね。そのことがよくわかる問題です。

では（１）いってみましょう。

step1　条件を発見する

問題文は以下の通りです。

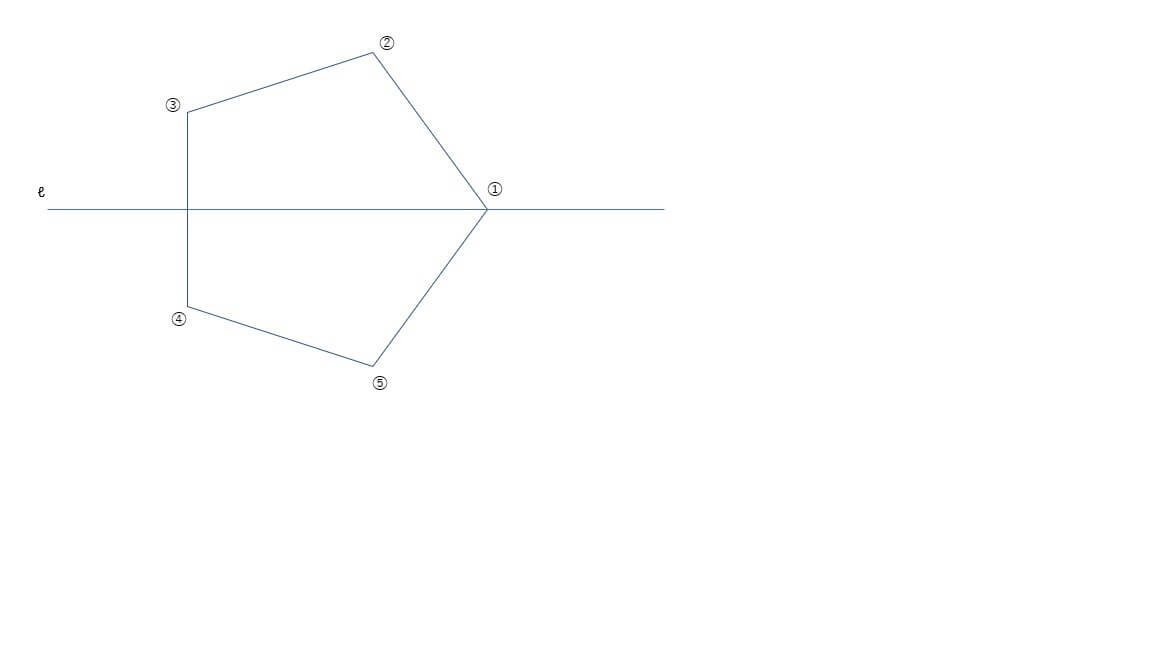
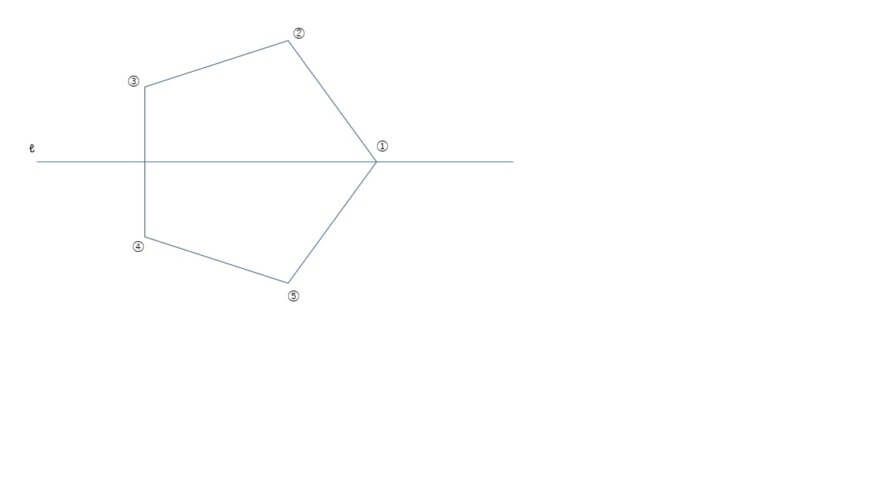
図の正五角形は直線ℓに関して線対称です。いま、点Aが正五角形の頂点①、②、③、④、⑤を、操作１、操作２、操作３のいずれかに従い移動します。

操作１：時計回りに２つ移動する

操作２：時計回りの反対の方向に1つ移動する

操作３：直線ℓに関して線対称な頂点に移動する

たとえば②からスタートして、操作１、操作２、操作３、操作３、操作１の5回の操作による点Aの移動は、次の例のように表記します。操作３、操作２、操作３、操作３、操作１による移動も同じ表記になります。

例：②　⑤　①　①　①　④

以下の問いに答えなさい（答えのみでよい）。

（１）点Aが②からスタートして2回の操作の直後にいることができる頂点をすべて書きなさい。

明示されている条件は、以下の通りです。ちなみに、問題を解くときには必ず条件に線を引きましょう。

操作１：時計回りに２つ移動する

操作２：時計回りの反対の方向に1つ移動する

操作３：直線ℓに関して線対称な頂点に移動する

そして重要な条件が他にもあります。

step2　隠れた条件を発見する

この隠れた条件に気づけるのかどうかが大問３の（３）を解くための重要なポイントになります。

その重要な条件とは、

操作１、操作２、操作３、操作３、操作１の5回の操作による点Aの移動は、次の例のように表記します。操作３、操作２、操作３、操作３、操作１による移動も同じ表記になります

これです。さらっと書かれていますが、これは重要な条件です。何を言っているのかというと、

操作手順ではなく頂点の移動経路を問う、ということを言っているのです。

（１）、（２）ではこの隠れた条件を利用することはありません。が、（３）では基本中の基本である問われていることの理解が必要になるのです。

受験生の中には頂点の移動経路ではなく、操作手順に着目してしまったかもしれません。問題文を正確に読み取れないと解答が出せないので、操作手順に着目してしまうと（３）は解答を導けません。

さて、今回は（１）ですのでさらっとやっていきましょう。

step3　解答の方向性を決める

2回の操作のパターンを場合の数により求め、そこから経路を導くことにより解くことができそうです。

これだけパターンが少なければ書き出してしまうのが最も確実性があります。

step4　解答の道筋を決める

2回の操作のパターンは、3×3で9パターン。9パターンそれぞれの経路を導き出していきましょう。

余計なことは考えずにとにかく洗い出します。

step5　計算する

１、１　・・・　②、⑤、③

１、２　・・・　②、⑤、①

１、３　・・・　②、⑤、②

２、１　・・・　②、③、①

２、２　・・・　②、③、④

２、３　・・・　②、③、④

３、１　・・・　②、⑤、③

３、２　・・・　②、⑤、①

３、３　・・・　②、⑤、②

力業で洗い出しました。

問題は2回の操作の直後にいることができる頂点ですから、①、②、③、④の4つです。

答えは①、②、③、④となります。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介