開成中学入試問題「算数」を徹底解説、平成28年度大問３（２）場合の数ー第16回

step1　条件を整理する

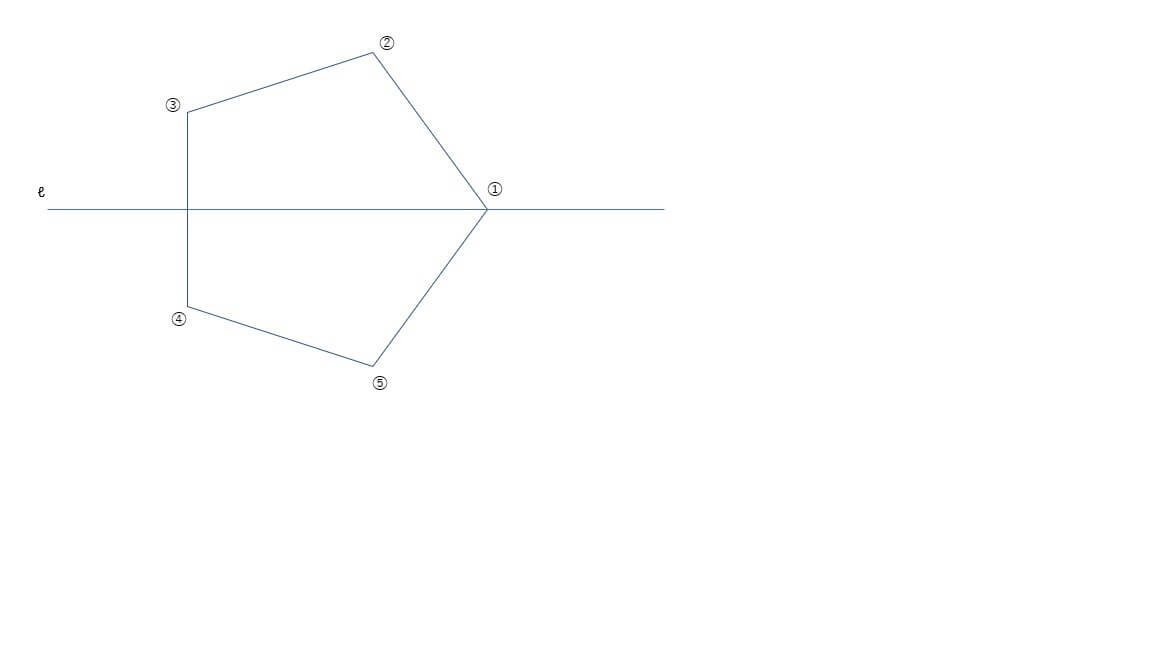
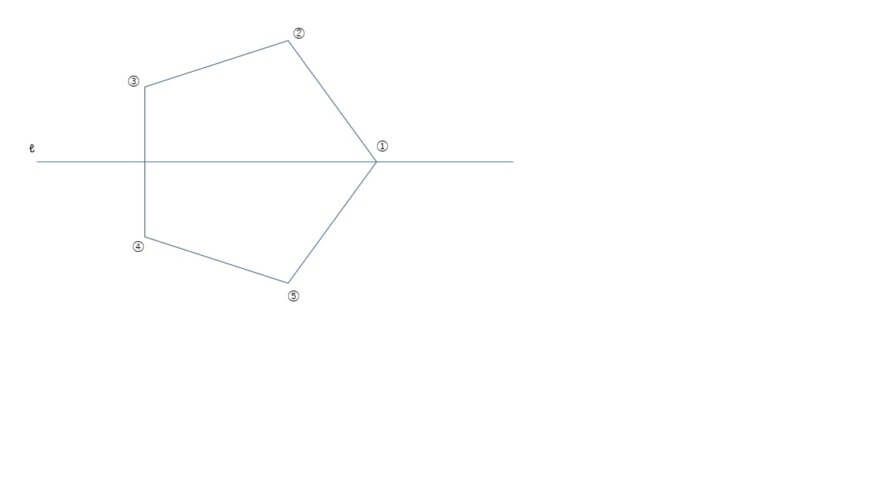
図の正五角形は直線ℓに関して線対称です。いま、点Aが正五角形の頂点①、②、③、④、⑤を、操作１、操作２、操作３のいずれかに従い移動します。

操作１：時計回りに２つ移動する

操作２：時計回りの反対の方向に1つ移動する

操作３：直線ℓに関して線対称な頂点に移動する

たとえば②からスタートして、操作１、操作２、操作３、操作３、操作１の5回の操作による点Aの移動は、次の例のように表記します。操作３、操作２、操作３、操作３、操作１による移動も同じ表記になります。

例：②　⑤　①　①　①　④

以下の問いに答えなさい（答えのみでよい）。

（２）1回の操作の直後に点Aが④にいられるような頂点をすべて書きなさい。

（１）と同じく条件は以下の通りです。

操作１：時計回りに２つ移動する

操作２：時計回りの反対の方向に1つ移動する

操作３：直線ℓに関して線対称な頂点に移動する

step2　隠れた条件を発見する

これも（１）と同じです。一応書いておきます。

操作手順ではなく頂点の移動経路を問う。

この問題ではこの条件は使いませんので、step2は不要です。

step3　解答の方向性を決める

問題は、

（２）1回の操作の直後に点Aが④にいられるような頂点をすべて書きなさい。

ということですから、操作１、操作２、操作３いずれかの1回の操作によって④にいられるような点Aを頂点を書き出して洗い出すことにします。エクセレントじゃない？エクセレントですよ。この問題において解答を導くための最短経路は書き出すことです。わざわざ問題を解くための手段を複雑化しないこと。シンプルイズベストです。

step4は抜かします。step3で方向性は求められており、step4を経るまでもなく問題を解くための方法が自明のものであるからです。

step5　計算する

操作１によって④に一回の操作で辿り着くためには、①の位置に点Aがいるしかありません。

操作２によって④に一回の操作で辿り着くためには、③の位置に点Aがいるしかありません。

操作３によって④に一回の操作で辿り着くためには、③の位置に点Aがいるしかありません。

したがって、答えは①、③です。

これは開成中学の親切心の現れのような問題

（１）、（２）の問題は（３）を解くためのヒント以外の何物でもありません。わざわざヒントをくれているのです。（３）では（１）、（２）で求められた条件と所与のものとして与えられている条件を使わないと解けません。

（１）、（２）は（３）を解くために必要だからわざわざ問題にしているのです。

この未知の問題においていきなり、（３）の問題を出したら解けるわけないと出題者が判断したのでしょう。

開成中学はとても親切な学校です。少なくともこの問題の出題者はとても優しいです。

これだけに限らず、未知の問題が出題される傾向がある開成中学においては、後に控える難しい問題を解くために必要な条件を問題として出題することが多いです。いきなり難しい問題に挑め、ではなく順を追って解いていくと解けるんだよ、という人間味のあるメッセージが問題からにじみ出ています。

こんな素敵な学校に入れた児童は幸せですね。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介