【中学受験】分配算・やりとり算　線分図の書き方、応用問題の解き方

誰が名前をつけているのか定かではありませんが、中学受験の世界では「〜〜算」なるものがいっぱい存在いたします。

分配算、やりとり算もその一つで、予習シリーズでは小学4年生で勉強いたします。

分配算、やりとり算とも線分図を使いつつ、2量、3量（あるいはそれ以上）の比に注目して解く方法です。

平たく言うと線分図を使って解く問題の一種です。

中学受験界の偉い先生たちは少し違ったやり方で解く問題が出てきたら、名前をつけたくて仕方なくなってしまうのでしょう。

いい感じの名前ならいいのですが、名前だけでは得体のしれない「〜〜算」も多くありまして、さだめし算数講師が酔っ払ってつけているに違いありません。

たとえば、ニュートン算。

中学受験を全然知らない人は「え？それって微積？」と勘違いすると思うんですよね。もちろん微積ではありません。

仕事算の一種です。

仕事をやってもやっても、上司が仕事を次から次へ押し付けてきたり、どこかのマヌケが仕事を失敗したりするのがニュートン算です。

あぁ、あとは栓を開きっぱなしの風呂に湯をはる問題とか。

こんなしょーもない計算に勝手に名前をつけられたニュートンも怒っていると思いますよ。

ちなみに30年くらい前も栓を開きっぱなしの風呂に湯をはる問題はありましたがニュートン算なんて大層な名前はついておりませんでした。

当時の四谷大塚の先生が「いいか、水が抜けていく風呂に何分で湯をはれるのか計算するやつは馬鹿だぞ。栓をしめろ！」となぜか怒って言っていたのを覚えております。きっと早く風呂に入りたかったのでしょう。

脱線しすぎました。

分配算、やりとり算です。

最初にも書きましたが、線分図を使って解く問題の一種です。それ以上でもそれ以下でもありません。

予習シリーズを使って学習している小学4年生は、すでに和差算、平均算、差集め算などの単元で線分図を学習済みですよね。

分配算、やりとり算では今まで習った線分図と比の考え方を使って問題を解きます。

楽勝っしょ！？

楽勝じゃない？なら、分配算、やりとり算の勉強をいったんストップして線分図を書く練習をしましょう。

分配算、やりとり算の線分図の書き方

一つ一つの単元には必ず目当てがあります。分配算、やりとり算では線分図と比の考え方の習得です。

そして線分図を書くスキルは「もう身についているよね？」という暗黙の了解があるんですよ。

ですから線分図の書き方については分配算、やりとり算の単元ではほとんど触れられていません。

このへんが算数の怖いところなんですね。

「前やったから書けるでしょ？」

と、四谷くんと大塚さんはズンズン進んでいきます。あぁ、最近はよっくんとか名乗ってるんでしたっけね。

まぁ四谷くんでもよっくんでもどちらでもいいです。

とにかく、「前やったところは分かっているはず」と毛の先ほども理解を疑ってくれないまま学習が進んでいくので、取りこぼしていると先に進めば進むほどどんどんやばくなっていきます。

皆様はよっくんの暴走にこれから2年半付き合わなくてはなりません。

ですから今のうちに線分図を書けるようにしておきましょう。この先たくさん使いますから。やっといて良かった、って思うようになりますから。

分配算　2量の比を線分図に表す（不足）

では、↓の文章を線分図に直してみましょう。

問い

駒込くんとお父さんの年齢の合計は53才です。お父さんの年齢は駒込くんの5倍より1才下です。お父さんの年齢を求めましょう。

↓が上の問いの線分図です。

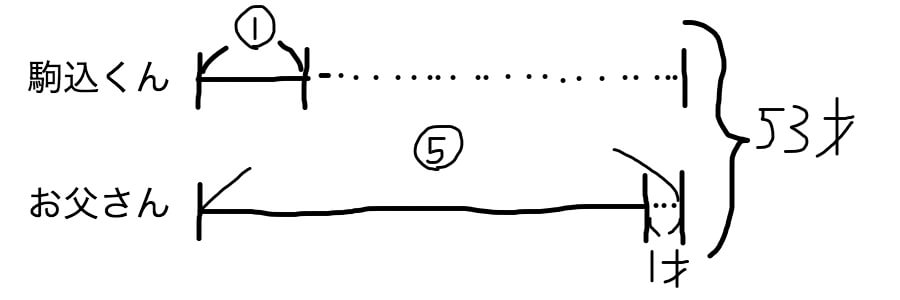
で、この線分図から、

（53+1）÷（①+⑤）=9・・・①

と①単位が求められまして、お父さんの年齢は、

9×⑤ー1＝44才

と求められます。

速すぎますね。でもたいていの塾ではこのくらいしか説明してくれません。ちゃんと線分図の書き方を教えてくれているんだとしたら先生に感謝したほうがいいですよ。

では予習シリーズに書いていない線分図の書き方のコツから説明します。

↓の線分図を見てください。カラフルに仕立てあげました。

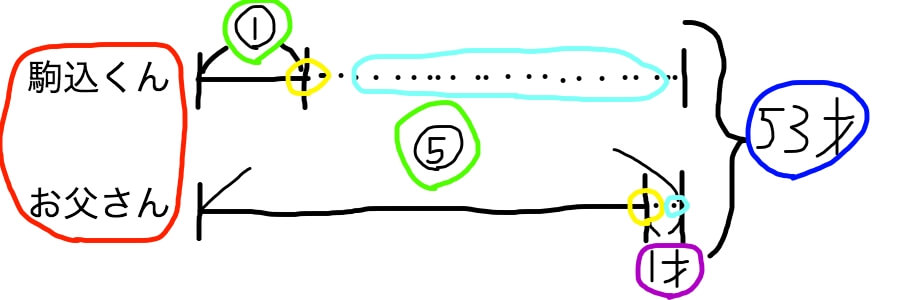
線分図の書き方の作法に色をつけていきました。

色別に説明していきます。

赤色の「駒込くん」「お父さん」

線のタイトルです。何の線なのか分かるようにしておきます。基本中の基本です。

黄緑色の①、⑤

①、⑤は比を表しています。

和差算や平均算、差集め算では比の概念が出てきませんでしたが、分配算、やりとり算では比の概念が出てきます。

上の問題で言うと「お父さんの年齢は駒込くんの5倍より1才下」という部分です。

駒込くんの年齢を①とするとお父さんの年齢は⑤ー1と表せますね。この概念はこれまでの線分図ではなかったものです。

必ず比は丸で囲みましょう。

これはルールでありドグマです。比は必ず数字を丸で囲む！

反論がある人は中学受験が終わってから言ってください。受験までは必ず丸で囲めや、コラ。

黄色の縦線

実線は実際の数量を表しています。実線の終わりには必ず縦線を引きます。

これをしておかないとどこまでが実際の数量なのかが分からなくなります。

ですから必ず書く。

水色の点線

点線部分は「不足」や「差」など実際の数量でないところを表しています。

実際の数量は実線、実際の数量ではない部分は点線。

実線と点線は必ず分けて書きます。

これもルールを決めてそのとおりに書かないと分からなくなります。

紫色の数字

比は丸で囲み、実際の数字（1才）は丸で囲まずに書きます。区別して分かりやすくしておきます。

で、ここで大事なのは単位も書いておくことです。

上の問題でいうと「才」です。「円」とか「cm」とか単位は色々ありますが、必ず単位を書いてくださいよ。

青色の数字

最後に全体の数量を書きます。全体の数量だから丸で囲みたい衝動を抑えられない？

絶対やめれ！

単位も忘れないでくださいよ。

線分図の書き初め

線分図を書くときに子どもたちがよく困るのは、

「最初にどこから線分図書けばいいのか？」

という点です。

勢い？

若気が至っておりますが、考えは至っておりませんね。

答えを言いましょう。

初めに書くのは基準となる数量です。

分配算の場合ですと、①となる数量から書き始めます。

つまり書き初めは、左に「駒込くん」と書きます。

ぐぐっと鉛筆に力を入れながらシャッと駒込くんの年齢を「実線で」書きます。

線の両端に「縦線」をしたためます。

上に「①」と結びの言葉を書き記すと大変縁起が良いです。

YO！

分配算　2量の比を線分図に表す（余る）

さて、上の問題ではお父さんの年齢は駒込くんの年齢の5倍より1才下でしたね。

今度はお父さんの年齢が駒込くんの年齢の5倍より5才上だとしたらどんな線分図になるのかを下に表しました。

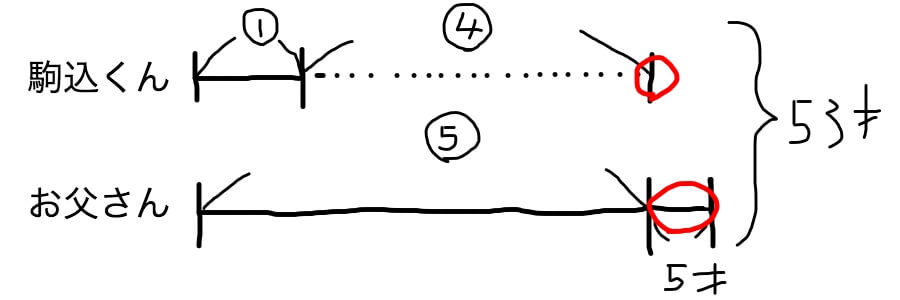
注目しておいた方がいいところを赤丸で囲っておきました。

「お父さんの年齢は駒込くんの年齢の5倍より5才上」なので⑤から5才だけ実線をひきます。

先ほどの「1才下」の場合は点線で書きました。

実際の数量は実線、実際の数量でなければ点線で書きます。何回も言いますがこれはルールです。法律です。

そして、駒込くんの点線はお父さんの年齢の最後までではなく⑤の最終地点までです。

分かりやすいところまで点線を引くというのが一番正しい言い方ですが、分配算の場合、基本的には大きい数量の比の最終地点まで引くと覚えておくといいでしょう。

短い線分図の点線は、長い線分図の最後まで引く、とかふわっと理解していると足元すくわれますよ。

やりとり算の線分図の書き方

分配算が終わるとさらっとやりとり算が出てまいりますが、こちらも線分図を書けるかどうかが勝負です。

では問題を解きながら説明します。

はじめ、AはBの4倍よりも150円多く持っていて、CはBよりも1100円多く持っていました。3人が同じ金がくずつ出し合ってゲーム機を1台買ったところ、Aの残りのお金は8000円になり、Cの残りのお金は、Bの残りのお金の3倍よりも200円少なくなりました。これについて、次の問いに答えなさい。

（１）ゲーム機を買った後、Bの残りのお金は何円になりましたか。

（２）ゲーム機の代金は何円でしたか。

引用元　予習シリーズ算数4年下　第2回分配とやりとりの問題　練習問題5（四谷大塚出版）　より

では、順を追って線分図を書いていきます。

まずは基準をA、B、Cの誰にするかという問題がありますね。

ここではゲーム機を買う前の所持金で線分図を書いていくことにしましょう。

すると、基準点はBと決めることができます。

なぜかって？

下の線分図を見てくださいよ。

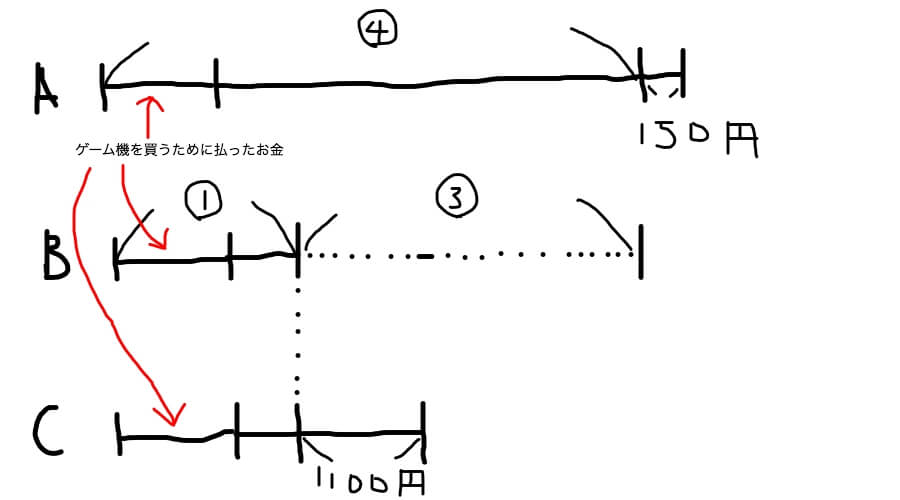
Bが比の①にあたりますよね。基本的には①の数量から最初に線分図を書きます。

さて、ゲーム機を買う前の所持金で線分図を書きましたが、これだけの情報ではBの残りのお金がわかりません。

では、ゲーム機を買った後のやりとりも上の線分図に書き込んでいきましょう。

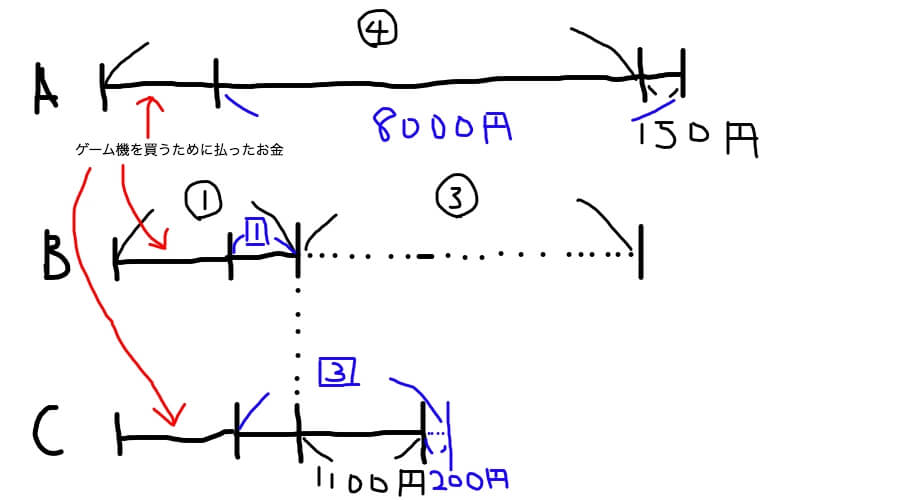
ゲーム機を買った後の情報を青で書きました。

ここで比を□で囲っている点に注目してください。

丸で囲ったのはゲーム機を買う前で、買った後の比は□で囲っています。

異なる比は異なるマークで囲みます。□でも三角でもどちらでもいいですが、普通は2番目の比は□で囲みます。

異なる比を異なるマークで囲むのは暗黙のルールでして、気の利いた先生は教えてくれます。

BとCの線分図を見てみますと、どうやら□の1が分かりそうですね。

そう、1100円と200円の合計が□の2と表せます。

これを式に表しますと、

（1100＋200）÷（3ー1）＝650円・・・□の1の金額

□の1はBがゲーム機を買った後の残金に当たりますから、答えは650円となります。

簡単でしょ？

問題をちゃんと整理して、図とか絵とか式に落とし込めれば中学受験の算数は簡単なんです。

でも整理するやり方を身につけるのが難しい、整理しないで解くのはもっと難しい。

問題が難しく見えるのは整理の仕方を知らないか、もしくは整理せずに解こうとするからなんですよ。でも本質的には簡単。

これは小学4年生の問題だけではなく、実際の受験問題にも言えることです。

実際の受験問題も基本に則って整理していけば簡単に解けるようになってます。

OK？

では次いきます。（２）です。「ゲーム機の代金は何円か」ですね。

もう一度、線分図に戻りましょう。

はい。

上の図の③の金額が分かりそうですね。

分からない？

よく見てくださいよ。

③は8000円から650円（□の1）と150円を引いた金額とイコールですよね？

①が求められそうです。これを式に直します。

｛8000ー（650+150）｝÷（④ー①）＝2400円・・・①

はい、①が求められました。2400円です。

で、Bがゲーム機を買うために支払ったお金は①から□の1を引いた金額です。

これを式に直します。

2400ー650=1750円・・・ゲーム機を買うためにBが支払ったお金

ゲーム機を支払ったお金は3人とも同じですから、

1750×3＝5250円・・・ゲーム機の代金

（２）の答えは5250円となります。

かわいそうに3人が買ったのはベッコベコにへこんだプレイステーション3です。

もう一度言いますが簡単ですよね？

やったことと言えばやりとりの様子を線分図に整理して、比の1単位を求める式を書き、あとは簡単な計算をしただけです。

受験も同じです。なぜこう言い切れるかって、古今東西の難関校の問題を解きまくったからです。

主に使ったのは条件整理、それから比です。ほんと、これだけ。

ただし、私、条件整理の方法はたくさん知っております。こういう場合にはこう整理する、ああいう場合にはああ整理する、とかいう知識があるから整理できるんですよ。

悪いことは言いません。条件整理の方法は覚えて使いこなせるようになっておきましょう。

小学4年生の9月まででしたら、代数分野は線分図とベン図は最低限使えるようになっておくと違いを見せられます。

よくね、基本をしっかりしておくと6年生の後半から急に伸びる（子もいる）っていうじゃないですか。

でも、基本が何なのか誰も具体的に言ってくれない、という謎のもったいぶり方も中学受験界の特徴でございます。

ってなわけであえて言いますよ、アチョー。

基本とは条件整理の方法です。

あ、言い過ぎました。身につけておくべき「基本」に基本的解法（例題レベル）も付け加えておきます。

条件整理（基本）ができるようになっていて、そこにプラスして応用のコツをつかみ急に成績が伸びるのが受験前の急激な伸びってやつです。

ただね、ほんと言うとですよ、受験まで半年を切った段階で打ち上がるかどうか分からないロケットを期待するもっと前にロケット打ち上げとけよとは思うんですけどね。

↓は応用問題の構造です。ご興味があれば。

【中学受験】応用問題の解き方・解くコツ　応用問題の正体とその対策法

あわせて読みたい

最新のホカホカ記事

書いている人の紹介