【中学受験】算数 倍数、公倍数、連除法、ベン図、倍数の利用
- 投稿日:2021.06.27
- 更新日:2021.10.12
- 予習シリーズ算数解説
- 中学受験, 倍数, 算数

初めて小学4年生の中学受験勉強に携わった方はご存知ないかもしれませんが、予習シリーズの旧版と新版ですと順序が結構入れ替わっております。
今回、まったりとお話を進めようと考えております倍数は、旧版では下巻の2回目で学習する単元でございます。
「えぇ!?新版の方が進みが速い!?中学受験の加速化?」
まぁまぁ、結論を急がずにヘソで紅茶を沸かしながらまったりとDevin the dudeでも聞いてくださいよ。
▼Devin the dude / doobie ashtray
確かに倍数については少しだけ早く学習しているかもしれません。
が、4年生全体のカリキュラムを見ますと、加速化というよりは順序の入れ替えと整理統合と言った方が良いのかと。
旧版と新版の4年生上巻の対比は↓で表にしております。総合回を抜いてますよ。
| 予習シリーズ算数4年生上巻 | 新版 | 旧版 |
| 第1回 | かけ算とわり算の文章題 | かけ算とわり算 |
| 第2回 | 計算のきまり | 角の大きさと性質 |
| 第3回 | 角の性質 | 計算のきまりと順序 |
| 第4回 | 和と差の問題 | 和差算 |
| 第6回 | 小数と単位 | 植木算 |
| 第7回 | 分数の性質 | 小数(1) |
| 第8回 | 三角形の角 | 分数(1) |
| 第9回 | いろいろな四角形 | 正方形と長方形 |
| 第11回 | 三角形の面積 | 大きな数とおよその数 |
| 第12回 | 間の数を数える問題 | 三角形の性質 |
| 第13回 | 周期を考える問題 | 周期算 |
| 第14回 | 等差数列 | 立方体と直方体(1) |
| 第16回 | 約数 | 等差数列 |
| 第17回 | 倍数 | つるかめ算 |
| 第18回 | 一方におきかえて解く問題 | 四角形の面積 |
| 第19回 | 立方体と直方体の性質 | 三角形の面積 |
これ見ただけじゃわかんねーよ、ってな文句も出てきそうですね。
実は新版は旧版の単元が2回分圧縮されています。
旧版の「大きな数とおよその数」が省略されているのと、旧版の「四角形の面積」が新版では「いろいろな四角形」に吸収されています。
理由は知りません。私、株式会社ナガセの社員じゃないですもの。
ただ、旧版の「大きな数とおよその数」は公立の小学校でも学習する内容で、大きな数の扱い方、以上や以下や未満の意味を知っていれば大した論理力は必要ない分野でございました。
また、旧版の「正方形と長方形」「四角形の面積」がなぜ分割されているのか大変疑問を感じておりました。
私はこの2つの単元を省略、合併されたのはお天道様に誓ってアグリーでございます。
また、旧版で幾何分野(図形とか)と代数分野(計算、文章題とか)が交互に出現する構成はちょっと学習しにくいよなぁと感じておりましたので、新版でその辺が整理されたのはとっても良いことだと感じております。
ちなみに旧版で学習された5年生も焦ることはございません。
ちゃんとあなた方も勉強してますから心配要りません。
ってわけで、加速化とか詰め込み、みたいな中学受験懐疑派がヨダレを出して喜びそうなトピックスをやっつけた上で今回の倍数でございます。
17回「倍数」ですが、新版では12回〜16回までの代数分野の続きです。別の言い方をすると、12回から16回までが前提となっております。
したがいまして、17回「倍数」を理解して解くには12回から16回までを理解していることが必要です。
さらっと書いてますが、私、結構怖いこと言ってますよ。
12回から16回をおろそかにしていると解けない、つまり、どこかで振り落とされていたら17回が理解できないんですよ。
これが算数の怖い点です。
算数は積み上げです。体系立った教科です。
1回、1回の基礎的解法と意味の理解を大事にしてのぞんで頂きますことを切に願っております。
中学受験ジェットコースターからゆめゆめ落とされないよう。
あ、落ちちゃったらジェットコースターとは言えませんよね。殺人マシーンです。
倍数の学習ポイント
倍数のポイントは4つあります。
1.倍数とはなんぞや
2.公倍数(最小公倍数)の求め方
3.「または」と「かつ」と「ではない」を理解する
4.倍数(公倍数)を利用する
ではそれぞれのポイントを意味の理解も含めてやっていきましょう。
倍数とはなんぞや
倍数がなんなのかって話ですが、単純な話です。九九を思い出してくださいな。
例えば5の段は、五一が五、五二十、五三十五・・・みたいなやつです。
いきなり、倍数とか言われると頭が混乱状態になって叫び出すお子さんもいらっしゃるでしょうが、
「九九を思い出せ」
その一言で冷静と情熱の間に引き戻すことができます。
ところがですね、九九を知っていても予習シリーズの例題レベルでいきなり意味不明なことになります。
こんな感じ。
150から250までの整数に3で割り切れる数字はいくつありますか?
パニックですよ。パニック。なんじゃこりゃ?って普通は思います。
割り切れる数字って?いくつ?もうわかんねー!
ってなってたとしたら正常です。
予習シリーズは昔からよく考えないと理解できない教材でございました。
では説明します。まずは思考過程から。
3で割り切れる数字は3の倍数です。
150から250までの数字を数えると101個あります。
3で割り切れる最初の数は150です。
3で割り切れる最後の数字は249です。
つまり、3で割り切れる最初の数と最後の数の間の数は249ー150で99個で、数えると100個あります。
150から250までの3の倍数は、最初が150で最後が249、公差が3の等差数列となっています。
したがって、249から150を引いて3で割った数に1を足すと3で割り切れる数の個数が求められます。
これを式に直します。
(249ー150)÷3+1=34
答えは34になります。
はい、これが思考過程です。
たった1行の問題を解くのに、こういった思考過程を経ます。
よく見てみましょう、この問題を解くのに必要なスキルを。
まず、約数で習った知識を使いましたね。3で割れるってことは3の倍数ですよね。
次に150から250までの数字を数えるとなんで101なんでしたっけ?引き算をすると「差」、つまり「間の数」が求められるますよね。「間の数」に1を足すと全体の個数になりますよね。これ、植木算の知識です。
最後に等差数列の知識を使ってますよね。3の倍数ってのは公差が3の数列なんですよ。
予習シリーズの12回から16回をよーく見てください。この一問を解くのに3回分の単元の知識を使うんです。ついでに言うと、等差数列ってのは決まりのある周期ですから、「周期を考える問題」も含めて正確には4回分です。
で、単純に暗記してるだけで知識を使えると思います?
使えませんよ。理解してないと。
「いやいや、問題解きまくって覚えりゃいいでしょ」
なんて考えますか?
何度でも言いますけど、それ、絶対に苦労しますから。
今、現時点で解ける解けないよりも、理屈を知って知識を使えるものにすることの方が大事ですから。
あるいは、上の理屈がよくわかんない。不安。というのであれば実際に数を書き出して数えてみてください。
34個ありますから。
馬鹿だと思います?
いいえ、実際に数えてみて「なるほど、確かにそうだ」と納得するのはとても大事ですよ。
わかんなかったら数えましょうよ。面倒臭がらずに。
算数は怖い科目です。
単に点数を取ってるからいいわけじゃないんです。
理解して点数を取っているかが大事なんです、後々のことを考えるとね。
「あ、これ、この前やった問題だ解けた!」
「こんな難しい問題、解けたのね!すごーい!」
演習量をこなして「見たことある問題を増やす」のも一時のカンフル剤としてはいいですよ。ヒロポンみたいなものです。
6年生、もしくは入試では見たことない問題が出てきますから。
全てのパターンを覚えるなんて無理です。
で、がっかりしているあなた。
大丈夫、今、点数低くても焦んな。
点数よりもどう解いているかを見とけ。
公倍数(最小公倍数)の求め方
最小公倍数を求めるのは連除法ですよね。
でも最大公約数を求める連除法とはちょっとやり方が違います。
では、いきましょう。8、12、16の最小公倍数を求めます。
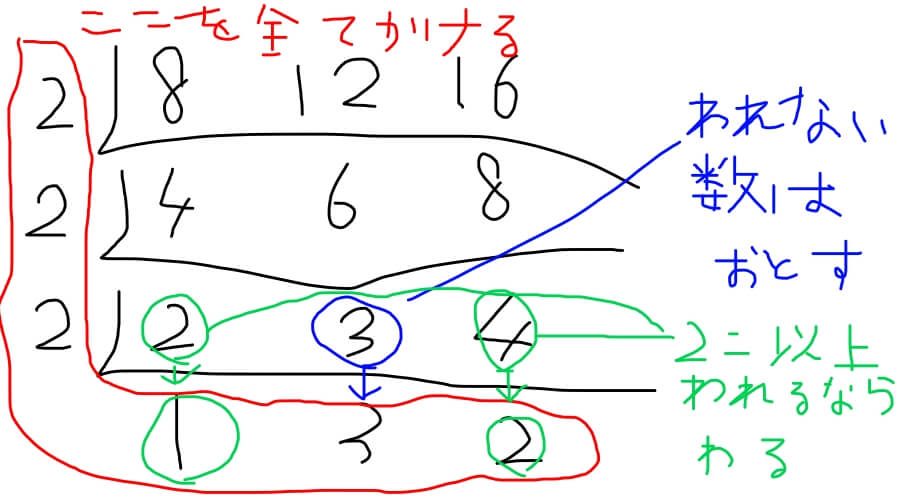
例によって素数で割ります。
で、最後の計算が最大公約数を求めるときと違いましたよね。
そう、3つの共通の約数じゃなくて、2つ以上割れるなら割る、と。
割れない数はそのまま下に落とす。
そういう風にして最終的に2つ以上の共通の約数がなくなるまで割り続けます。
最後に赤で囲った部分を全部かける。
これが最小公倍数を求めるときの連除法です。
こんなもんは覚えちまえばいいです。
さっきと言ってることが違うって?
うーん、覚えるだけでいいことと、理屈も含めて理解しないといけないことがあるんですよ。
連除法は前者、覚えるだけでいいことです。
いいから、さっさと覚えろ、それでいいんです、連除法については。もちろん理屈はありますが、混乱しますし時間もかかります。
「または」と「かつ」と「ではない」を理解する
これ、情報系の授業とかでやりませんでした?あるいは数学とか。
やってない?そりゃ覚えてないだけです。
これ、情報系の授業では論理演算やブーリアン演算とかいう名前で教えてくれたはずです。数学では論理。
中学受験の分野では「ベン図」を使って論理の概念を学習します。難しい言葉は出てきません。
ちなみに「または」は論理和とか言われています。
「かつ」は論理積。
「ではない」は色々なパターンがありまして、否定と否定論理和、特に倍数の単元では否定論理和をよく使います。
では1から100までの数のうち12の倍数と16の倍数の集合をベン図で表してみます。
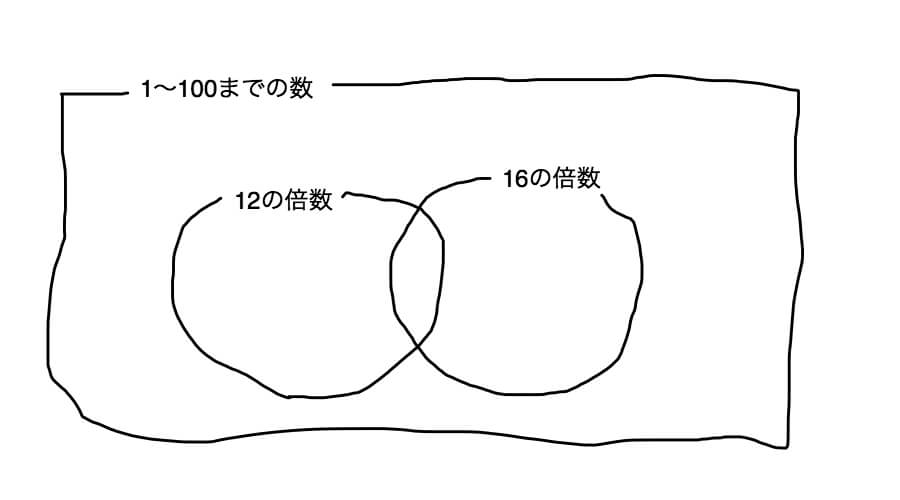
上の図の「12の倍数」の丸の中を「12の倍数の集合」と呼びます。
同様に「16の倍数」の丸の中を「16の倍数の集合」と呼びます。
このベン図で「または」、つまり「12の倍数と16の倍数の集合」(論理和)はどこに当たるのかというと下の図の赤い斜線部分です。
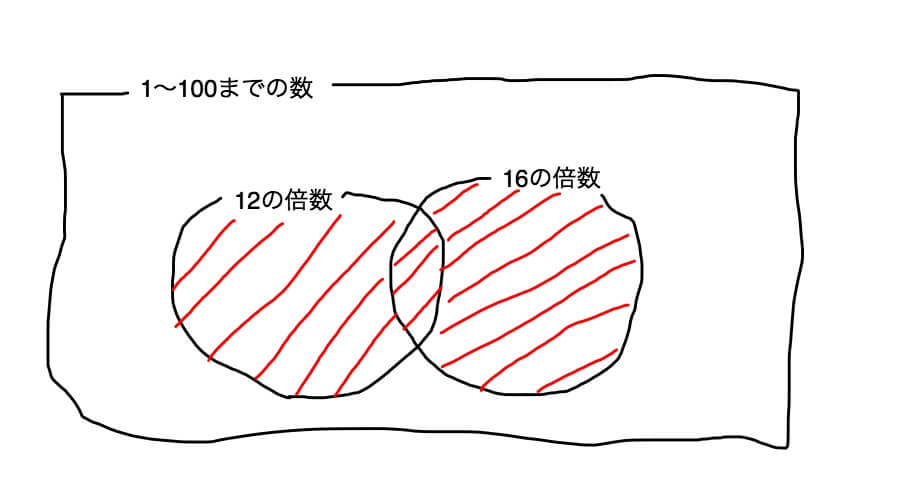
では、上の赤い斜線部分に含まれる個数(集合の要素の個数)を求めましょう。
100までの数字のうち、12の倍数は8個あります。「100÷12=8・・・4」で求められます。
16の倍数は6個あります。「100÷16=6・・・4」で求められます。
8個と6個を足すと14個になるのですが、ここから公倍数を差し引かないといけません。
なぜなら「12の倍数の集合」と「16の倍数の集合」の共通部分がダブルカウントされているからです。
12と16の最小公倍数は48です。
100までの数字の中に48の倍数は2個あります。「100÷48=2・・・4」で求められます。
14ー2=12となり、答えは12個と出てきます。
「かつ」はすでに求めてますね。集合の要素の個数は2個です。「12の倍数と16の倍数の共通部分」(論理積)、つまり公倍数です。ベン図で表すと以下の斜線部分です。
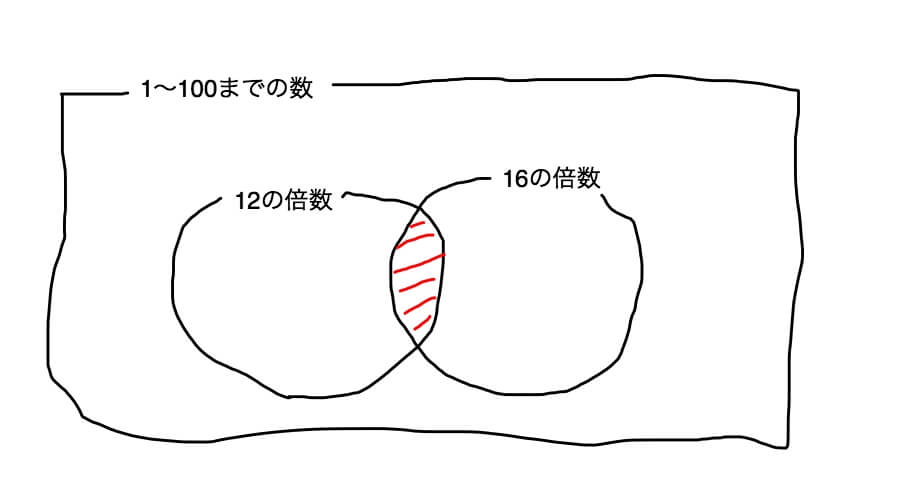
次に「12の倍数でも16の倍数でもない部分」を求めます。別の言い方をすると否定論理和です。
以下のベン図の斜線部分です。
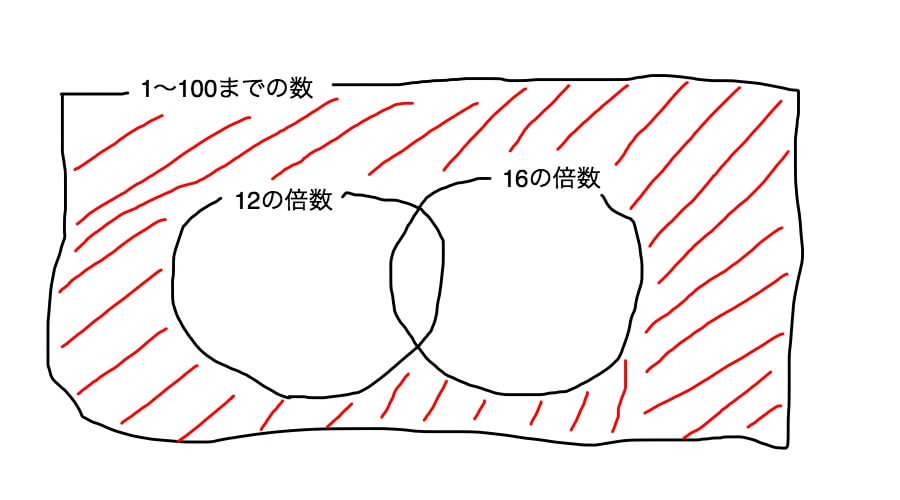
この斜線部分は1から100までの数字から「12の倍数かつ16の倍数」(論理和)を引けば求められます。
式にしますと、
{(100ー1)+1}ー12=88
で、88個と求められます。
「え?何で {(100ー1)+1} なんて意味不明の計算してるの?」
なんて疑問がムクムクするかもしれません。
これは1〜100までの要素の数を求めております。
そんなん100に決まってるだろ、と思われるかもしれませんが、では「0から100までの要素の個数」は?
100個?なわけないでしょう。
答えは101個です。
要素の個数は差(つまり、間の数)に+1をして求められます。植木算でやりましたね。
ですから {(100ー1)+1} なんて計算をしているんですよ。
ここを省いて「100までなんだから要素の個数も100!」なんて雑に扱っていたりすると、「0から100までの要素の個数」が101個になる理由が分からなくなります。
さて、ベン図を使うと含まれるもの含まれないもの、重複しているものが視覚的に理解できます。
テストで直接出てくるところではないので軽視しがちですが、ベン図の考え方はめちゃくちゃ大事です。
倍数を利用する
さー、出ました。利用、です。つまり応用。
ここまでが予習シリーズの例題、類題です。つまり、応用も含んでいるんですね。
12回から16回までで培った知識や理解をフル活用して解くんです。
先ほども申し上げましたが、予習シリーズは単にやり方を暗記すればいいって教材じゃありません。
前回、あるいは前々回も含めた理解を前提にした例題、類題が出てくるんです。
だから難しい。
ただし、きちんと各単元で学ぶ知識を理解していれば、知識と知識、理解と理解がつながる感覚が味わえる最強のテキストです。
まぁ、いいです。問題にいきましょう。
指導主事が用意したストロングゼロをAくん、Bくん、Cくんに4缶ずつ配っても、12缶ずつ配っても、16缶ずつ配っても余りが出ませんでした。このとき次の問題に答えなさい。
(1)指導主事が用意したストロングゼロは最も少ないときで何缶か答えなさい。
(2)指導主事が用意したストロングゼロが500缶以上700缶以下のとき、最も多い缶数を答えなさい。
(3)指導主事はAくん、Bくん、Cくんになぜストロングゼロを配ったのですか。20文字以内で答えなさい。
※指導主事 学校の教員が試験を受けて就く職種。主に教育委員会に所属していて、教員に指導を行う立場の者。
用例)来週の研究授業であの指導主事が来るんだよ〜、あの人掲示物が好きだから壁に学級目標とか貼っておかなきゃな!
はい。
(1)は連除法を使えば一瞬です。ただし、問題文の意味を把握しなければなりません。
4缶、12缶、16缶配っても余らなくて、かつ最も少ないときですから4、12、16の最小公倍数を求めりゃいいってことを問題文から把握しなくちゃならないんです。
連除法の使い方よりも、どんなときに使うのか、それを問題文から読み取るのが難しいんですよね。
小学4年生ですらこれですから6年生になったらヤベェですよ。
今のうちに問題文を理解する練習をしておきましょう。
さて、4、12、16の最小公倍数を求めればこの問題の答えは出ます。
連除法のやり方は割愛いたします。
答えは48缶です。
結構飲ませるな、この指導主事。
(2)はちょいと難しいですよ。
最小公倍数が48ですから、500以上700以下の48の倍数になります。
こういう時はむやみやたらに500以上の48の倍数を求めるんじゃなくて、500を48で割ります。
500÷48=10・・・20
48缶ずつ10回配っても余りが出ますので、10よりも多い回数です。
つまり48缶を11回配った時です。
48×11で528になりますね。これが500缶から700缶の間で指導主事が配って余りが出ない最小の数です。
ここで求めるのは700缶以下の最大の缶数です。
さて、どうやって求めましょうか。
一番簡単なのは、528に48を足していく方法です。
576、624、672、720
最も大きい数は672ですね。
答えは672缶。
最大の数値が小さかったらこれで求められます。
では大きい数だったら?
問題の最大値が10000缶だったとしましょう。
この場合の主体は指導主事ではなくサントリーの社員です。
10000÷48=208・・・16
つまり、48缶ずつを208周期繰り返すことになります。
48×208=9984缶
答え 9984缶
この手の問題は大きい方の数で割っちゃうといきなり最大の数値が求められます。
でもこれは教えない方がいいかもしれません。自分で気づくのを待つ方がいいかと。
算数は苦労した方がいいんです。
指折って数えたり、ノートに数字を書き出したりして、苦心惨憺の上、「あぁー!」と気づくまで待つのが中学受験の算数での親御様の正しい態度です。
(3)いきます。
指導主事は普通、教員のことを「〜くん」とは呼びません。「〜先生」と呼びます。
したがって、Aくん、Bくん、Cくんは教員ではないと推察されます。
すると、Aくん、Bくん、Cくんは児童もしくは生徒です。
ただし、20歳未満はストロングゼロを飲めない立て付けになっておりますので、この指導主事は県教委に所属しており、高校を担当していると見るのが普通です。高校ならば留年がありますから。あるいは通信制で通学している高校生です。
2年以上の留年、もしくは通信制の20歳以上の高校生に対してストロングゼロを振る舞う指導主事の気持ちを想像しましょう。
「一緒に飲もうぜぇ・・・!辛いことは忘れてぇ・・・!」
で、あります。
すると一人に48缶もストロングゼロを配布した指導主事の痛いほど切ない心情が浮かび上がってきます。
答え「人生の辛さを分かち合いたかったから」
みんな辛いんだよ。
頑張れ・・・、中学受験生、ならびに月ごとに財布が軽くなっていく保護者の方々。
私も文章書くの辛いんです。
でも、とにかく決めたんです。あと、2年は親御様に伴走していくと。
頼りないけど信じておくれ。
あわせて読みたい
最新のホカホカ記事
最新のホカホカ記事の一覧はこちらから書いている人の紹介
星一徹のプロフィールはこちらから- 前の記事

【中学受験】約数、約数の個数、素数、最大公約数と連除法(はしご算) 2021.06.18
- 次の記事

【中学受験】算数 つるかめ算、弁償算(一方におきかえて解く問題)の理屈 2021.07.04

