【中学受験】算数　等差数列を極める3つのポイントと公式

さぁ、4年生の親子は共々打ち震えるがいい！

等差数列の登場でございます。

植木算（間の数を考える問題）、周期算ときて等差数列、やっと中学受験らしくなってきましたね。

この3つの学習単元はつながってますから、いずれかの理解が不十分ですと等差数列の問題はきちんと理解して解けません。

では、等差数列を解くために何を身につけておくといいのか。

ポイントは3つです。

1.順番を求めているのか、間の数を求めているのかに意識的になること

2.公式（パターン）を暗記すること

3.周期を発見すること

この3つのスキルが身についていると4年生レベルの等差数列は大体解けます。

3はわかりやすいですよね、周期を発見しなくては始まりません。

で、経験上、4年生レベルだと結構これはできるんですよ。

2の公式暗記。

これは暗記するだけです。暗記パンでも食っとけ。

最もつまづく可能性が高いのは1です。

周期の発見はできた、公式も暗記している、でも一体今何を求めるんだっけ？で、求めるためにはどうするんだっけ？

1はいわゆる使いこなし方に関するスキルです。

公式や周期の発見は道具にすぎません。

その道具をどう使うのか、それが重要なのであります。

ここでですね、ぜひやっていただきたいのが面倒でも周期を書くこと、そして式を立てることです。

式を勃てるだけで1回分くらい書きましたが、この時のために書いたと言っても過言ではございません。

【中学受験】算数で式を書かないのはなぜだ？式を書く大事さ

式を立てるとたくさんいいことがあります。

普通の人の頭はたくさんのことを同時並行処理できるようにできていません。

ですから順番にこなしていかなくちゃいけませんが、1、2、3・・・と処理をしていくと3番目の処理をするときに「はて？1で何やってたっけ？」ってな話になるんです。

ですから、古くはパピルス紙に託宣を書き綴っていたように、中学受験生も途中計算式を書く、と。

こうやって自分の思考を紙に書いて論理力を涵養するって寸法です。

これは人類の知恵です。私の浅はかな知恵ではございません。

式を書くともう一ついいことがあります。

「これを求めるにはこうやって式を書いて・・・」と求めるべきことに対して意識的になれるんです。

さて、4年生の学習はまだまだ初歩の初歩です。

式なんか書かずに解けるかもしれません。

でもね、断言しますが式を書かないクセをつけたまま応用問題、難問にがっぷり四つしても簡単に上手投げをくらいます。

「あれ、今何を求めるんだっけ？何を求めてるんだっけ？」

算数は論理を組み立てる力が重要です。

論理力は式をきちんと書くことによって身につけられます。

論理的に過程を積み上げて解くのをおろそかにした結果、4年生、5年生で偏差値60以上とってた子が6年生になってズンズン追い抜かされていく様子を見てきてますから、とにかくやっとけと。

さて、等差数列です。

例によって問題を解きながら親御さんのために解説していきますよ。

お子さんには見せないでください。

時々、私、卑猥な言葉を差し込んだりしますので。

等差数列の基本を暗記しよう

2つ暗記しといた方がいいことがあります。

これ、予習シリーズに書いてますからね。私が発掘した解き方じゃありません。

1.等差数列の□番目は「最初の数＋公差×（□ー1）」である

2.等差数列の和は「（最初の数＋終わりの数）×個数÷２」である

じゃあ、それぞれ実際の問題を解きながら説明していきますよ。

等差数列の□番目と□番目までの和を求める

問題です。

ある決まりにしたがって

2、5、8、11、14・・・

と並べたときの30番目の数を求めなさい。

また、30番目までの数の和を求めなさい。

 

30番目の数を求める式：（30ー1）×3＋2＝89

答え　89

 

30番目までの和を求める式：（2＋89）×30÷2＝1365

答え　1365

暗記した公式通りに解けましたね。超基本問題です。

ただ、油断してると大変です。

頭の中だけで解こうとしちゃってたら赤信号。赤信号みんなで渡れど不合格。

ちゃんと書いて整理しなさい！

とお子さんにソフトタッチで語りかけていただけると私が睡眠不足を被った甲斐もあるというものです。

では整理の仕方を説明していきます。

まずは数列を書きましょう。あと、公差も。

2、5、8、11と書いて間に「3」と書き込むんです。いえ書き込ませるんです。

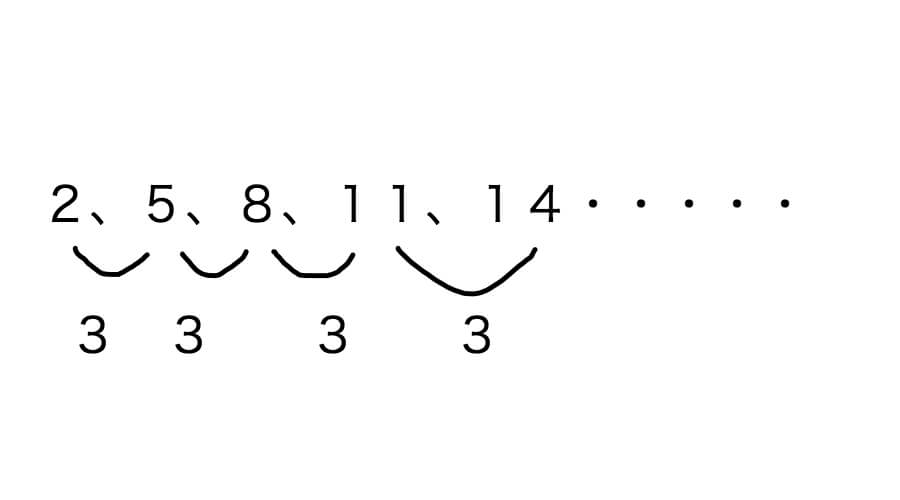
こんな感じです。

すると以下のように条件整理ができます。

条件整理①：公差は3である

条件整理②：最初の数は2である

上記の条件整理をして公式を当てはめる・・・、まあそれもいいんですが、暗記した公式が一体何をやっているのかもついでに理解しておきましょうよ。

私は次のような式を書きました。

（30ー1）×3＋2＝89

まずはですね、なんで30から1を引いていると思います？

これ、間の数を求めてるんです。

植木算でやりましたよね？

両はしに木が植えてある時は間の数は「木の本数ー1」になるって。

【中学受験】植木算とのりしろ問題を絵で攻略する

で、等差数列における公差ってのは間の距離なんですよ。植木算でいうところのさくらとさくらの木の間の距離なんです。

だから間の数に間の距離をかけると全体の間の距離が求められるんです。

この問題では公差、つまり間の距離は3でしたね。

すなわち間の数「30ー1」の答えと、間の距離の3をかけると全体の間の距離が求められるんです。

最後に足した2は最初の数です。

間の距離は求めましたが、「−1」をすることによって最初の数の「2」が抜けちゃってるんです。

なので最後に2を足します。

すると、30番目の数が求められるわけです。

では次に和を求めましょう。↓が式。

（2＋89）×30÷2

公式通りですね。

ではここでもなぜ公式が成立するのか見ていきましょう。

例えば、

1、5、9、13、17、21

という等差数列があったとします。

公式に当てはめるとこれらの数字の和は、

（1＋21）×6÷2＝66

になりますね。

疑り深い方は一つずつ足していってみてください。

なるでしょ？

どうしてそうなるのかを下に示します。

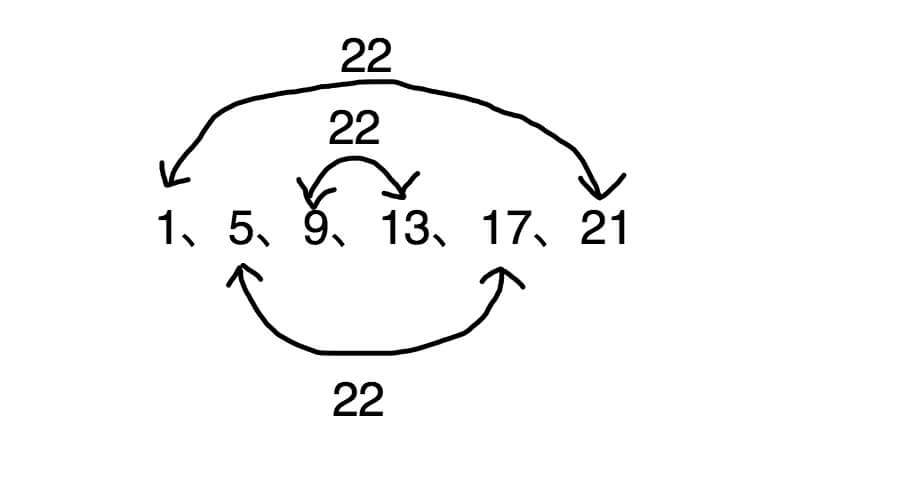
等差数列の最初の数と最後の数、前から2番目の数と後ろから2番目の数・・・を足すと一緒の数になるんです。

この足された2つの数を1セットとすると、上の例では1セットで22。

ということは全体の個数を2で割って、最初の数と最後の数を足したものをかけると全体の和になるんですね。

公式を暗記するのも大事ですが、どうしてそうなるのかロジックを理解すると洗練されます。頭が。

多分、こういったロジックは塾で教えてくれると思いますけど、仮に教えてくれなくて悩んでいたとしたら親御さんが説明できるようにしておくといいと思いますよ。

奇数の等差数列の和を求める

予習シリーズには奇数の等差数列の和の求め方も書いてます。

最近のテキストは親切ですね。むせかえるようなおもてなし精神で溢れかえっております。

覚えといた方がいいですけど、上であげた等差数列の和の求め方でも十分対応できます。

では一応説明しときます。

問題

以下の数列の和を求めなさい。

1、3、5、7、9、11、13

 

式①：7×7＝49

式②：（1＋13）×7÷2＝49

答え　49

式①のように、1から始まる奇数の等差数列の場合、「個数×個数」で全体の和が求められるんです。

もちろん、式②のように等差数列の全体の和を求める公式に当てはめても同じように答えが求められます。

ではなんで式①のように1から始まる奇数の等差数列の場合「個数×個数」で全体の和が求められるかっていうと、乗数の性質を利用しているからなんですね。

1、4、9、16、25、36、49、64、81

と1の二乗から9の二乗まで並べてみましたが、間の数の規則性を見てみてくださいよ。

3、5、7、9、11、13、15、17

になってますね。

つまり、平方数（二乗の数）の間の数の規則性は1、3、5、7、9、11、13という奇数の数列と同じなんです。

1番目は1

2番目は1＋3で2の二乗と一緒

3番目は1＋3＋5で3の二乗と一緒

というように二乗の数の間の数の規則性と同じになってるんです。

だから、1から始まる奇数の数列の和は□番目の二乗と同じになります。

ただ、これはマル秘テクニック。

袋とじのようなものです。

基本は等差数列の和は「（最初の数＋終わりの数）×個数÷２」と覚えておけば対応可能です。

ちなみに旧版の予習シリーズ「等差数列」には1から始まる奇数の等差数列の和の公式は載っておりません。多分、最近になって必要性に駆られたんでしょうね。やるな、株式会社ナガセ。

ここまでは超基礎です。

だからとっても大事です。ぜひ例題をしっかり覚えて例題と同じように類題を解いてください。

さ、ここまでマスターしましたら最大の難関である「順番を求めているのか、間の数を求めているのかに意識的になること」を身につけるだけです。

等差数列、何を求めているかに意識的になること

では問題を解きます。

問い

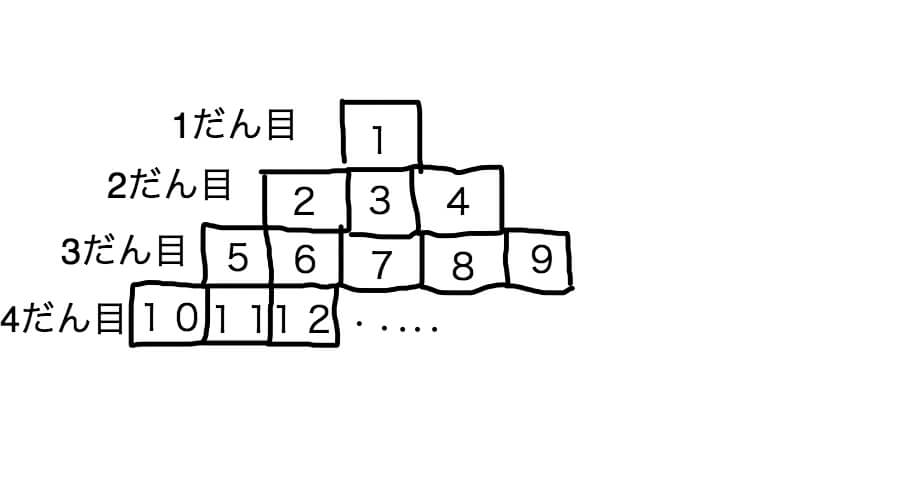
図のように、階だんの形にならべた正方形に、1から順に整数を書きいれていきます。これについて、次の問いに答えなさい。

（１）1だん目から12だん目までに、正方形は全部で何個ならんでいますか。

（２）12だん目の正方形にかき入れた整数の和はいくつになりますか。

（１）の解答

式：（12ー1）×2＋1＝23

（1＋23）×12÷2＝144

答え　144個

 

（２）の解答

式：{1＋12×（12ー1）}×23＝3059

答え　3059

出典：予習シリーズ算数　4年上　第14回「等差数列」練習問題５　より

等差数列（１）の問題を解説

まずは条件整理です。

条件整理①：正方形の数は段数ごとに1、3、5、7、9・・・という等差数列になっている

条件整理②：公差は2である

この問題は1段目から12段目までの正方形の数の和を求める問題ですから、1段目の正方形の数と、12段目の正方形の数がわかれば解けますよね。

なので、12段目の正方形の数を求めるぞ、と方針を決める。

何を求めたいのかをはっきりさせることが本当に重要なんです。

では、式を立てます。

（12ー1）×2＋1＝23

上の式から12段目には23個の正方形があることが分かります。

この式の意味は12ー１で間の数を求め、×2で公差をかけて間の距離を求め、最後に1を足して12段目の正方形の数を求めている、と。

最終的に求めたい答えを出すために、過程で何を求めているのかを意識しながら式を書く。

等差数列の公式自体は1年経ったら忘れているかもしれません。

が、過程で何を求めているのか意識すること、これはやればやるほど上手になります。

しかも算数の他の単元でも役に立つ、基盤となる力です。

どっしりとした土台にレンガを積み上げていけば堅牢な家ができあがります。

算数御殿を建立していきましょうよ。

次に1段目から12段目の正方形の和を求めます。

これは公式に当てはめればいいだけ。

（1+23）×12÷2＝144

答えは144個です。

ちなみにこの問題には別解があります。

12×12＝144

答え　144

1から始まる奇数の等差数列は□番目を二乗すると、□番目までの和が出ましたよね。

あっさり答えが出ますので気分がいいに違いありません。

ただ、私は公式を当てはめりゃOK、解けりゃOK、って結局近道なようで遠回りに思えるんですよね。

だからこの解き方はあんまり好きではありません。

過程を考えて、求めるものを意識して、一つずつ式を立てて解く。いかにも遠回りです。でも算数で大事な論理力を身につけるにはあえて遠回りするのも一興。

4年生のお子さんをお持ちの親御さん方が「遠回りしといて良かった〜」と思える日は600日後くらいにきます。そう遠くない未来の話です。

等差数列（２）の問題を解説

これも条件整理をします。

条件整理③：各段の数の合計は真ん中の数に正方形の数をかけて求められる

条件整理④：各段の真ん中の数は1、3、7、13と規則性のある数列になっている

条件整理⑤：間の数は2、4、6と偶数の数列になっている

条件整理⑥：つまり、真ん中の数は『1＋（段数ー1）×段数』で求められる

上の条件から真ん中の数と12段目の正方形の数が求められれば12段目の数の合計が求められますよね。

で、12段目の真ん中の数は、

1＋（12ー1）×12＝133

となります。

12段目の正方形の数は（１）の問題で求めた通り23個です。

つまり、真ん中の数の133に23をかけると12段目の数の合計が求められます。

133×23＝3059

答え　3059

となります。

私はこのように解きましたが、着目するポイントによって解き方が変わってきます。

大事なのは、

着目するポイントを特定して、

条件を整理して、

規則性を見出し、

何を求めればいいのか意識しつつ、

式に落とし込む。

慣れれば一瞬で下のような式を立てて計算して終了です。

{1＋12×（12ー1）}×23＝3059

どうしたらいいかって？

何回も訓練するしかないです。

きちんと条件を書く。何を求めればいいのか明確にする。式を書く。

等差数列のまとめ

何事も練習です。

どんな練習をすると等差数列が得意になるのか下に書いておきますよ。

1.与えられた条件を整理する

2.数列を見つけ出す

3.数列を書き出して公差を見つける

4.規則性を見出す

5.求めるもの（数なのか和なのか等）を意識する

6.公式に当てはめて式を書く

7.計算する

ちなみに私が中学受験で好きなのは比と条件整理ですが数列もその次くらいに好きです。

だって綺麗じゃないですか、規則性のある数列。

規則性のある数列みたいに世の中も綺麗だといいなぁ、としみじみしながら溜まりに溜まった洗濯物を睥睨する午前0時30分。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介