【中学受験】小学4年生「割合の基礎」　割合の教え方とコツ、出た！最重要単元

小学4年生で習う最重要単元が「割合」でございます。

「割合」を制する者は中学受験の代数分野を制する、と勝手に私は申し上げますが、それくらい重要な単元なのであります。

なぜかって？

割合に続く、速さ、グラフ、食塩水、比・・・。これらは割合の概念を理解していないと理解できないからです。

さらに言いますと、割合の考え方って中学の数学、あるいは高校数学における代数の基礎になるんです。割合でつまづくとこの先の算数→数学までずっと苦労します。

サッカーで言うところの止めて、蹴る。

新日本プロレスで言うところのヒンズースクワット。

会いに行けるアイドルで言うところの秋元康。

で、予習シリーズには皆さん大好き、割合の公式が書いてあります。

1.割合＝くらべる量÷もとになる量

2.くらべる量＝もとになる量×割合

3.もとになる量＝くらべる量÷割合

「さぁ覚えろ、これが算数・数学の基礎だ！なに？便利なやり方？くもわだ！」

と、まぁ、これまた皆さん大好きな公式の暗記とくもわなのでありますが、普通の小学4年生はこんな説明ではさっぱり分かりません。

公式の暗記やらくもわを使って一発で割合を理解できる小学4年生は普通ではありません。相当センスあります。

ではどんな風に教えるのか、そしてコツは何なのか。

結論から先に言いますと、「イメージをつけさせる」です。

割合を使いこなせる子って割合の肌感覚やイメージを持ってるんですよ。

文章題を見て、何がくらべる量でもとになる量で割合なのかをウンウン考えずにササッと把握して、公式を使わずに解く、と。

できる子からすると、公式がどうちゃらこうちゃら思い出して解く方がよっぽど難しいんです。

じゃあ、できない子はどうなるのって、公式を覚えさせるとさらにワケわからなくなります。

できない子にとっては地獄っすね。

しかしながら、大人の感覚からするとどうして我が子が割合が分からないのかが分かりません。

そこで、まずは最初に我が子が割合を分からない感覚を味わってもらう「ドSスタイル」でいきます。

微分係数を求めてもらいましょう。

微分係数を求めてみましょう

さぁ、数Ⅰまでしか履修していない文系ペアレンツの皆さん、微分係数を求めましょう。

なに？どうやって求めればいいか分からない？

HAHA！では親切な私が公式を授けましょう！

はい。

微分の初歩中の初歩の問題です。問いも明瞭、親切な公式もあります。

さぁ解きましょう！簡単ですYO！

関数f(x)＝x^2＋xを親切な公式に当てはめればいいんです。

答えは3になりますね。

これで微分係数の求め方、分かりましたか？

理系の人は分かると思いますが、文系で数Ⅰまでしか履修していなかったら分かるわけがありません。

「そもそも微分係数ってなんだよ？」

「limってなんだ？だいたい、limの下にh→0とか書いてあるのが意味わかんねぇ！」

そんな文句が聞こえてきそうです。

では、何を求めているのかグラフにしましょう。

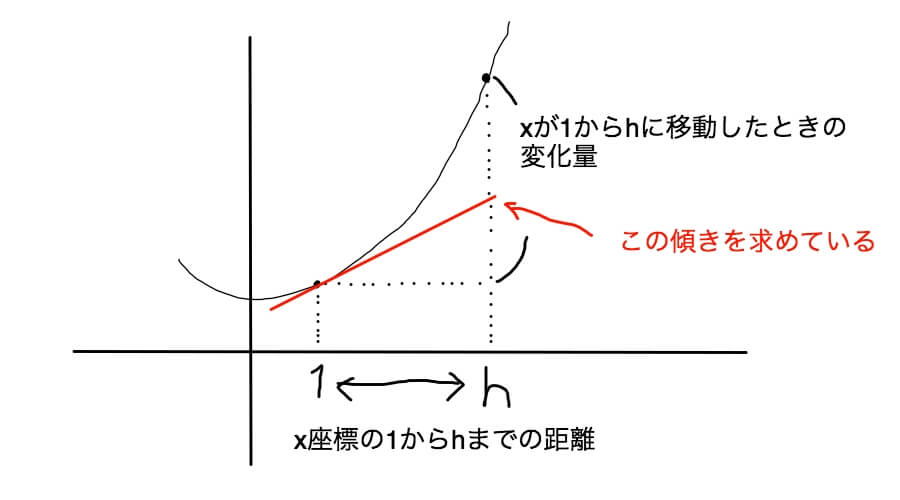
微分係数とか難しそうな言葉を使いましたが、要は傾きのことです。

で、親切な公式を使うとある1点における傾きが求められるんです。

分からない？

そりゃそうです。微分を習ってない人は分からなくて当然です。

私、微分がどういうときに使われるものなのかも説明してませんし、それぞれの用語の意味も、公式がなぜ成り立つのかも、傾きなんか求めてどうなるのかも、なーんにも説明してませんもの。

でもね、公式と何を求めているのかと答えは提示しましたよ？

これ、

「割合の公式（あるいは「くもわ」）を使うとくらべる量、もとになる量、割合が求められるのだ！だから答えが出るだろう！なんでわからないんだ！」

って、熱烈ペアレンツの叱咤激励と似てません？

今までに習ったことのない単元を抽象度の高い教えられ方をすると全く分からない現象が発生します。

なんでわからないのかって、ちゃんと教えてないからです。そんな教え方なら最初からしないほうがいいです。

叱咤激励とか無駄ですから。

叱咤激励って、きちんと教えられない人がキレてるだけなんですよね。

で、割合って単元はこれまでの単元に比べるとやや抽象度の高い単元なんです。

ですから、分かりにくいんです。とくに小学4年生には。

ちなみに、微分は一定変化しない定量的な現象のある1点における加速度を求めています。

微分を使うと、

・オオタニさんの打った打球がスタンドに入る手前の速度

や

・80度でいれたほどよい感じのコーヒーが5分後にどのくらい冷めてしまうのか

や

・煮え切らないあいつが「結婚しよう！」と言うまでの時間

を求めることができます。

あ、すみません。「結婚しよう！」と言うまでの時間は積分を習わないと求められませんね。失礼しました。

1 2 3 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介