【中学受験】植木算とのりしろ問題を絵で攻略する

植木算です。

中学受験を経験された親御さんでしたら

「ワッホ！全部の木から1引くやつでしょ！」

とウキウキされていらっしゃるかもしれません。

ところで最近の予習シリーズでは「間の数を考える問題」と称されているようで、控えめに「植木算」と書いてあります。

いいですね、名称が本質的です。

さて、この植木算（間の数を考える問題）、四谷大塚および四谷大塚NET加盟塾、早稲田アカデミー、の小学4年生は5月くらいに学習します。

SAPIXではもっと早くて3月くらい。予習シリーズより早めに学習していくのはTAPからの伝統か。30年前の日曜教室でもTAPの子らは早めに学習して上位をかっさらっていきましたからね。ついでに四谷大塚の優秀層までかっさらっていっておりました。

日能研はカリキュラムが本質的すぎて植木算をいつやってるのかわかりません。

さて、植木算は前にも書いたような気がしますがぶっちゃけ予習するのが難しいと思ってます。

理解のコツは3つ。

1.基本パターンの暗記

2.絵を描く

3.何を求めているか意識する

それぞれいてこましていきますよ。

植木算の基本パターン

まずは基本パターンの暗記です。

いきなり本質的じゃないこと言いやがってと思われるかもしれません。

が、まずは暗記、次に理解。

さて、植木算の基本パターンは大きく分けて2つです。大した量じゃありません。覚えちゃいましょう。

1.まっすぐに木を植える

2.まわりに丸く木を植える

まっすぐに木を植えるパターンの解き方

まっすぐに木を植えるパターンは、

1.両端に木を植える

2.両端に木を植えない

この2つに分かれます。

両端に木を植える場合、木の本数から1を引いた数が間の数です。

240mの道路の端から端まで同じ間隔で5本さくらの木を植えました。さくらの木の間の距離を求めましょう。

式：240÷(5ー1)=60

答え　60m

両端に木を植えない場合、木の本数に1を足した数が間の数です。

240mの道路に同じ間隔で5本さくらの木を植えました。さくらの木の間の距離を求めましょう。ただし、両端に木は植えないものとします。

式：240÷(5＋1)=40

答え　40m

大事なのは間の数を求めてるってこと。

植木算を理解するポイントは間の数です。木の数じゃありません。

ここがややこしいんですよね。

下手に植木算とか言われるから木の数、木の数・・・と木にばっかり注目してしまうんですが、本当は間の数に注目した方がいいんだよ、と10歳の頃の私は調子に乗って分からない子に教えていたものです。

なぜ間の数に注目した方がいいのかはあとで数直線を使って説明します。

まわりに丸く木を植えるパターン

まわりに丸く木を植えるパターンは木の数と間の数が一緒になります。

なのでこうなります。

240mの池の周りに同じ間隔で5本さくらの木を植えました。さくらの木の間の距離を求めましょう。

式：240÷5=48

答え　48m

簡単ですね。

まとめますとこうなります。

次にこれを丸暗記したあとで実際に絵を描いてイメージしていきます。

普通の小学4年生は文字だけじゃよく分かりませんからね。

植木算の絵を描く

絵を描きましょう。

もっと正確に言います、絵を描かせましょう。

算数はイメージできるかが大事ですからね。

はい、では上にあげたパターンごとに絵を描きます。

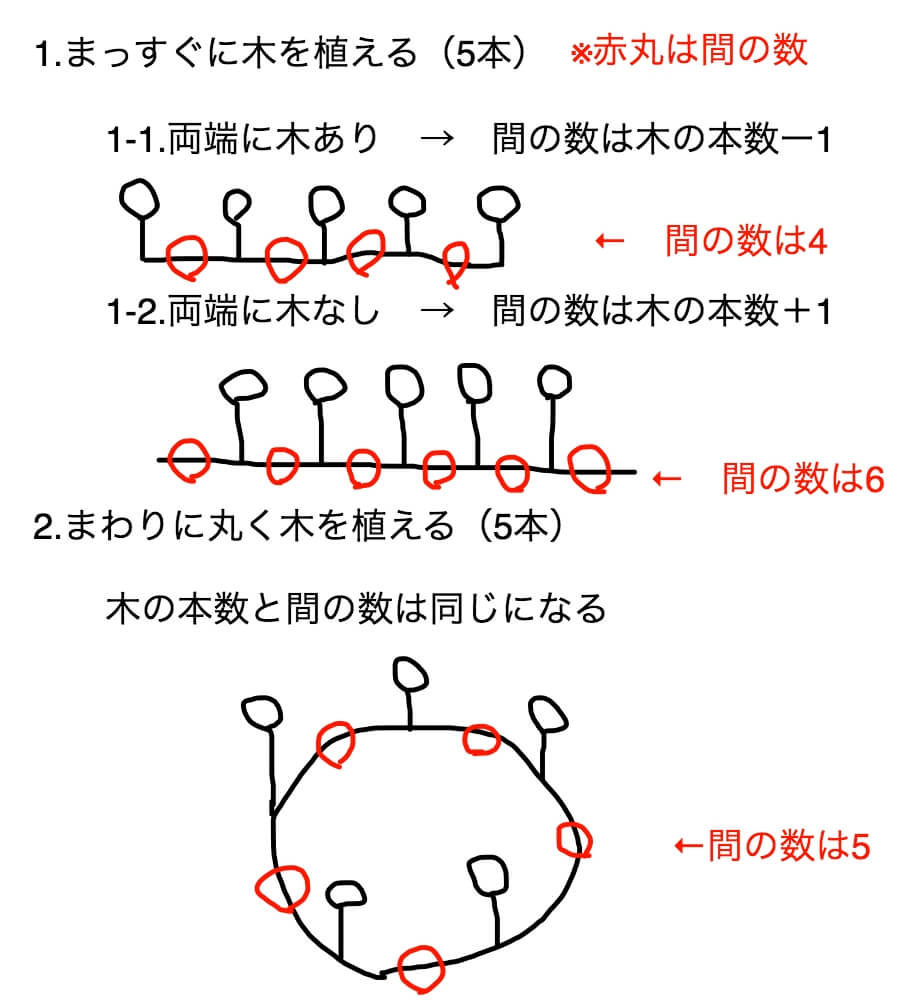
小学生のうちは文字からイメージを膨らませるのが大人よりも苦手です。

なので絵を描きます。算数は絵です。

すみません、言い過ぎました。

暗記と絵でイメージができたところで問題です。

240mの道路の端から端まで同じ間隔で5本さくらの木を植えました。2本目のさくらと4本目のさくらの間の距離を求めましょう。

式：240÷(5ー1)=60、60×(4ー2)=120

答え　120m

さて、出ました。

単純に木の本数に1を足したり引いたりという知識だけでは解けない問題です。

式を分解して見てみます。

240÷(5ー1)＝60

↑は木と木の間の距離を求めています。基本パターンの暗記でいけますね。

60×(4ー2)＝120

↑は木と木の間の距離に、2本目の木と4本目の木の間の数をかけて距離を求めています。

2本目の木と4本目の間の数？？？

単純に基本パターンだけ暗記していると2本目の木と4本目の木の間の数の求め方が分からないキッズが続出します。

「2本目と4本目の木の間の数の求め方なんて基本パターンにないじゃねぇか！」

いやいや、基本パターン通りです。

植木算を難しく感じるのは基本パターンで何を求めているのか理解していないからです。

間の数を求めているんですよ。

何を求めているのか意識する

では、2本目と4本目の木を絵で描きます。

必ず絵を描きます。いえ、描かせます。何だったら指を使ってみても構いません。

問題文や数、式を頭の中で具体的なイメージに変換する訓練が「絵を描く」こと。

しつこく訓練すると、そのうち問題文から具体的なイメージが頭に浮かぶようになりますから。

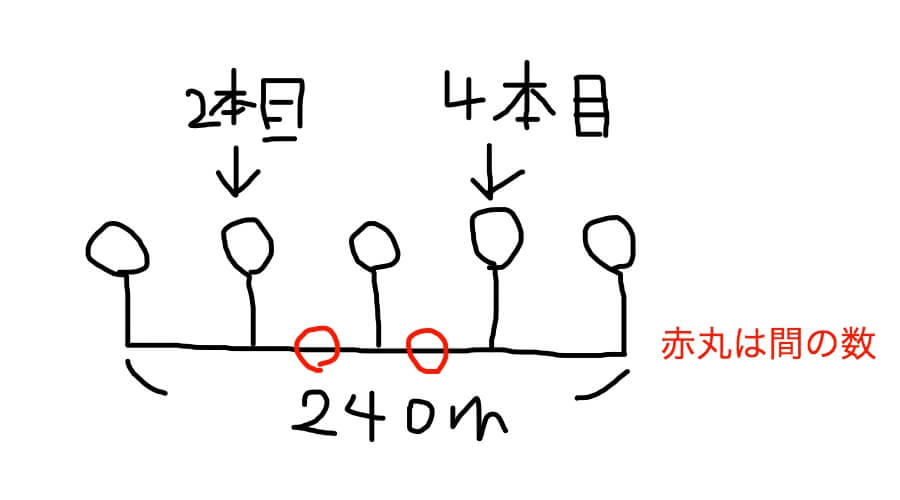
ほら、2本目の木と4本目の木の間の数は「2」って分かりましたよね。

４から２を引いても「2」って出てきます。

では、そもそも４から２を引くってなんですかね？

引き算って何をしてるんでしょう？

引いてる？

いえ、引かれる数と引く数の差を求めているんです。つまり、間の数。

小学校の教科書にもちゃんと書いてあります。

先生の説明も聞いているはずです。

ただ、差を求めるってのがどういうことか分かっていない子供多数。

ちなみに私はいろんな道具とプリントを使ってゲロが出るくらいしつこく説明します。

さて、数直線を描きます。

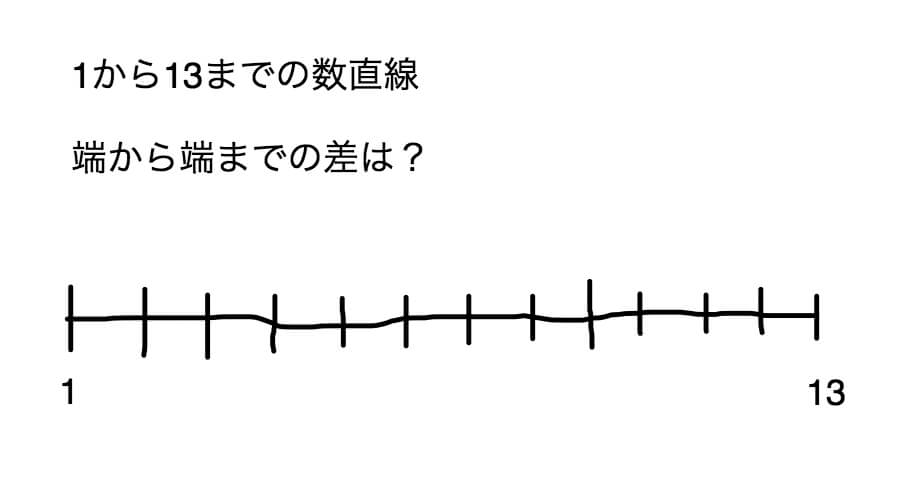
間の数を数えてみてください。

12ですよね。

式で表現すると13ー1＝12

つまり、間の数ってのは引き算で求められる差のことです。距離と言ってもいいかもしれません。

植木算によく似てますよね。

植木算では木に置き換えて数直線の概念を勉強してるんです。

余談ですが数直線の概念が分かるとマイナスの数で引くときにプラスになる理由も分かります。

6ー（ー４）＝１０

みたいなのです。

↓で割と詳しく説明してますのでご興味があれば。

【中学受験】引き算ってなに？　マイナスの数で引くとプラスになる理由と植木算の関係

植木算　のりしろの問題

植木算の派生パターンとして他にのりしろの問題もあります。

問題です。

20cmの紙が5枚あります。これを3cmののりしろでつないでいきました。長さは何cmになりますか？

解答パターン①：（20ー3）×2＋（20ー6）×3＋（5ー1）×3＝88

あるいは

解答パターン②：20×5ー（5ー1）×3＝88

あるいは

解答パターン③：20＋（20ー3）×4＝88

答え　88cm

これも絵を描きます。

最初からスマートに解こうなんて、お天道様は許しても高橋英樹が許さない。

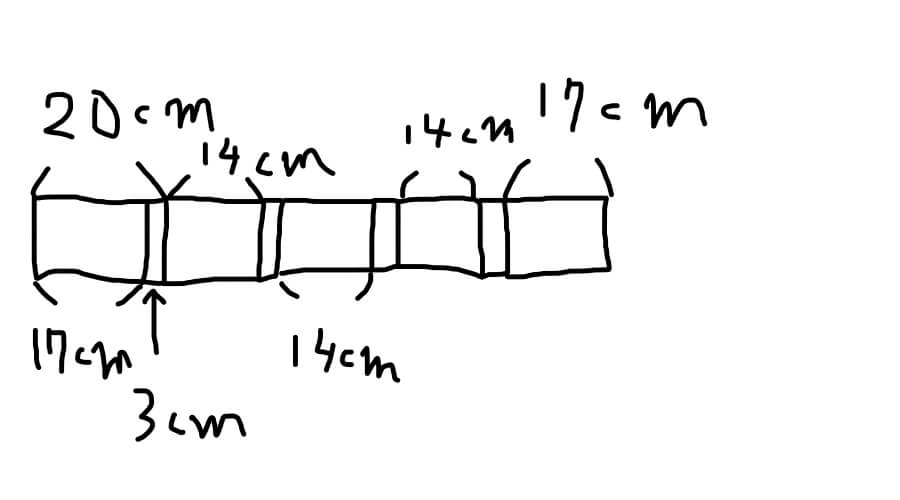
パターン①の式は全部足していく力技です。

両はしの紙の長さ、間の紙の長さ、のりしろの長さを合計しています。

（20ー3）×2＋（20ー6）×3＋（5ー1）×3＝88

パターン②の式はテキスト推奨パターン

5枚の紙の長さの合計からのりしろの長さを引いています。

20×5ー（5ー1）×3＝88

パターン③の式は規則性に注目しています。

左はしの長さとその他の紙の長さを足しています。

20＋（20ー3）×4＝88

それぞれ答えを出す過程は違いますが、全て同じ答えになりましたね。

植木算の考え方を使ったり規則性の考え方を使ったり。

イメージを具体的に持つことができると色々な観点から問題を解けるようになります。

なお、テキストの推奨パターンは②ですし、私もこれが一番シンプルだと思います。

が、こんな応用問題になるとどうでしょう？

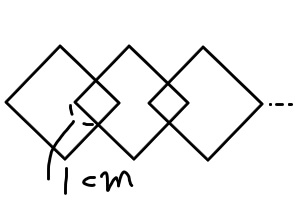
1辺が3cmの正方形の紙を下の図のように重ね合わせました。全体の面積が121㎠になるのは紙が何枚あるときですか？

式：（121ー9）÷8+1＝15

答え　15枚

↑の解き方はパターン③の規則性に注目した時の解き方を利用しています。

もしパターン②の推奨パターンのみを丸暗記して無理やり解こうとすると、

□×9ー（□ー1）×1＝121

9□ー□＋1＝121

8□＝121ー1

８□＝120

□＝15

お世辞にもキレイな解き方とは言えません。

つーか、マイナスをマイナスする概念や文字式、移項の技術が必要ですから方程式を習ってないと解けません。

いろんな解き方を考えるのは大事ですよー、とよく言われる理由は一つの解き方だけ覚えても解けない問題が今後いっぱい出てくるからです。

で、いろんな解き方を考えるための第一歩は考えるための道具を使って具体的にイメージすること。

今回は絵を描きました。

次は何を描くでしょうか。

素晴らしい未来予想図を描けるといいですね。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介