【中学受験】算数　つるかめ算、弁償算（一方におきかえて解く問題）の理屈

さぁ、出てきました、鶴と亀。

その昔、つるかめ算と称されていた問題は新版予習シリーズでは「一方におきかえて解く問題」と、とても本質的なネーミングに変更されております。

願わくば、「一方におきかえて差に注目する問題」と、とっても本質的なネーミングにして欲しかったのですが、まぁいいでしょう。

以前、つるかめ算については書いたと思いますが、つるかめ算は一方におきかえて１単位ずつ変化させた時の合計の差に注目して解く問題でございます。

また意味の分からないことを言っていると思われるかもしれませんね。

つるかめ算は皆様もご存知の連立方程式でも解けるのですが、中学生は忙しいのでXとYを使って代入法や加減法といった方法を駆使して解いていたりします。

ただ、中学生は忙しいあまり、とりあえず変数をXとYとして、代入法や加減法に当てはめて解いちゃったりします。

ちっとも本質的ではありません。

齢4つ、5つほども違う小学生が理屈を理解して解かなきゃいけない問題を、中学生が方法論に当てはめて解いているわけでして、そりゃあ中学生の頭も悪くなるわけでございます。

え？一方におきかえて解く方法に当てはめるんだから中学生と同じでしょ！？

なーんて、思わないでくださいよ。

やり方の意味も分からずに解くのは道具の使い方を知らずに道具を使うのと一緒で全く応用がきかなくなります。

解けるからいい、なんて考えるのでしたら中学受験の算数はやる意味がないです。

せっかくですから、どっぷり浸かりましょう。

中学受験算数のコクの深さ、奥行きに。

つるかめ算の理屈、一方におきかえて解くとは一体なんぞや

では問題いきましょう。

20円のプリキュアチョコレートと50円の仮面ライダーラムネを合わせて20個買い、760円ちょうど支払いました。プリキュアチョコレートと仮面ライダーラムネは何個ずつ買いましたか？

簡単すぎますね。

式を勃てます。

(50×20-760）÷（50-20）＝8

20ー8＝12

答え　プリキュアチョコレート　8個、仮面ライダーラムネ　12個

一瞬で出ましたね。

よく分かっていない塾の先生、主にバイトの先生は、

「すべての個数を一方におきかえて解いたときは、もう一方の数が求められるんだぁー！」

と威勢良く唾を飛ばしますが、「なんで？」という疑問には少しも答えてくれません。

え？高い金払って某アカデミーに通っているのに先生が若すぎる？

お察しいたします。

例えば、上の例で言いますと仮面ライダーラムネを20個買ったと仮定しますから、もう一方のプリキュアチョコレートの個数が8と求められたのですが、どうしてそうなるのかは教えてくれません。

まるで菅首相の緊急事態宣言のようですね。

うーん、そもそも一方におきかえるって、どういうことでしょうか？

表を書いてみると分かりますよ。

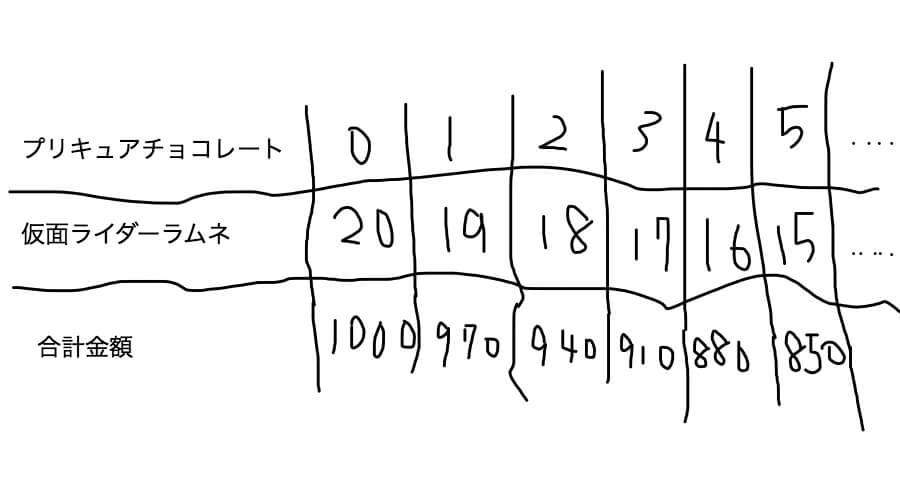
上で勃てた式（20×50＝1000）では仮面ライダーラムネを全部買ったと仮定しましたよね。

つまり、上の表の左端、プリキュアチョコレートを0個、仮面ライダーラムネを20個買った時の合計金額を求めております。

で、次はそれぞれの商品を１単位ずつ変化させた時の合計金額の変化に注目してみましょう。

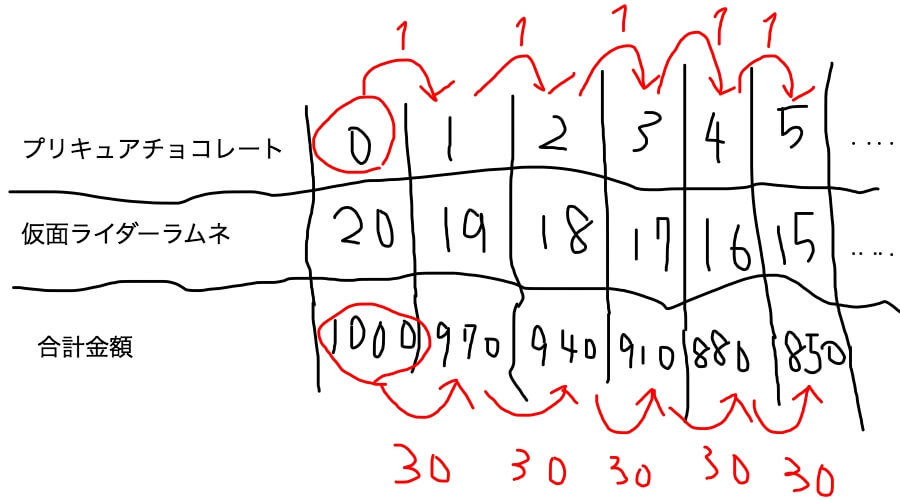
プリキュアチョコレートの数を1個ずつ増やしていくたびに、合計金額が30円ずつ減っていきますね。

1単位ずつ変化させると、合計金額の差が30円ずつ変化していくんです。

ということは、全て仮面ライダーラムネを買った時の金額と実際に払った金額を引いて30で割ったら、プリキュアチョコレートを0個買った時からの個数の差が求められますよね。

で、これが8なんです。

0地点から8単位変化させますので、プリキュアチョコレートは8個ってわけ。

全部で20個買ったのですから、20ー8＝12で仮面ライダーラムネの個数も求められます。

これを図にしてみましょう。

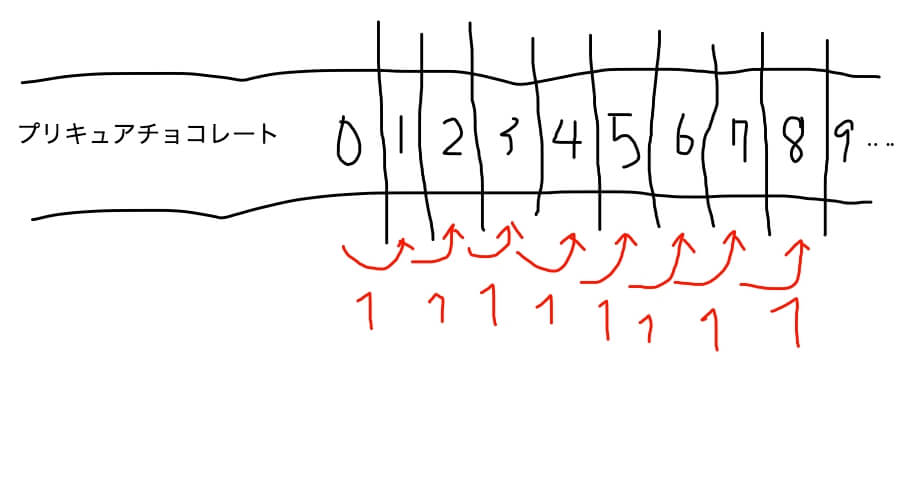
ほら、プリキュアチョコレートが0個の地点から8個移動させると8になりましたよね。

つまり、つるかめ算ってのは一方に全部をおきかえた時に1個ずつ数量を変化させていった時の差に注目して解いているんです。

このような理屈で、おきかえた数のもう一方の数が求められる寸法なのでございます。

弁償算も考え方は全く同じですよ。

弁償算の理屈

弁償算ってのはこんな感じの問題です。

四谷くんはお皿を1枚洗うと50円もらえますが、割ってしまうと30円払わなくてはなりません。20枚のお皿を洗った時に四谷くんは何枚か割ってしまいましたが、520円もらえました。四谷くんは何枚のお皿を割ってしまったでしょうか。

（50×20ー520）÷（50＋30）＝6

答え　6枚

もうね、センスないからお皿洗うのやめたほうがいいよ、四谷くん。

と、ボンクラの四谷くんに代わってホシザキ先生の登場を待つような状況でございます。

ホシザキ株式会社ウェブサイト

これ、つるかめ算と全く同じことをやってるんですよ。

鶴と亀の足の差は2本でしたね。

では、お皿を洗った時と割った時の差はいくつになりますか？

答えは80円です。

これも図に表してみましょう。

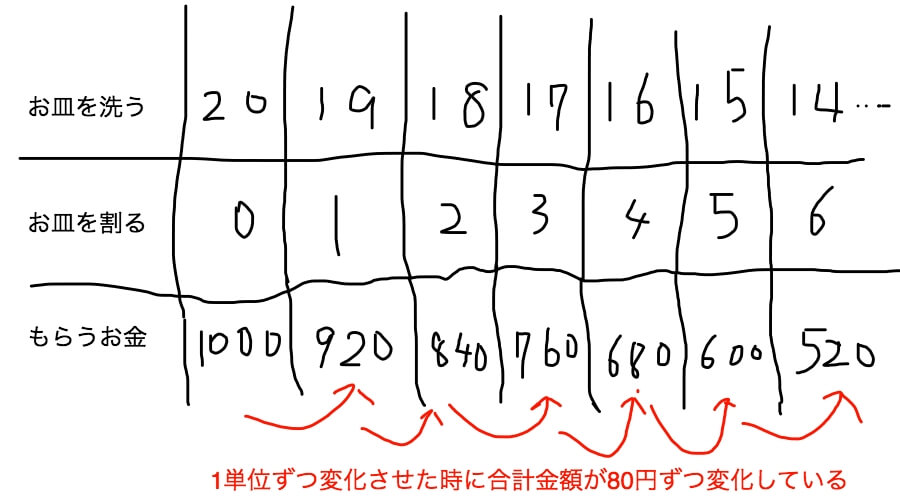
合計金額の差は1000ー520で480円。

1単位変化した時の差は80円。

つまり、480÷80で80で6単位変化したことになります。

したがって、お皿を6枚割ったことになります。

四谷くんは初日でバイトをクビになるはずです。

差とは？

差というのは、ある地点からある地点までの間の数のことです。

0から6までですと、6ー0で6が差と求められます。

1から6までの差は5。ただし、要素の数は6。植木算でやりましたね。

【中学受験】植木算とのりしろ問題を絵で攻略する

新版小学4年生予習シリーズ上巻の第12回から第18回までは差に注目しまくりました。

第12回で植木算を学習した理由は以降の単元で間の数、つまり差の概念を利用するからです。

いきなり植木算（間の数を求める問題）が出てきて面食らった方もおられましょうがきちんと理由があるんです。

え？おたくのご息女、ご子息はつるかめ算と弁償算を分けて覚えて解いている？

お茶目ですね。あるいは若気の至りでございます。

同じ問題ですよ。つるかめ算と弁償算は本質的に同じ問題です。

それもこれも、なんとか算とか名前付けしちゃってるからでありまして、正しくは「一方に置き換えて差に注目しろ」という一喝でどうにかなるのであります。

最近、「理屈を理解しなさい」、と書きまくっておりまして大変疲れてきたところであります。なんでそんなこと意識するのかいまいちわかんねぇという親御さんの嘆きも聞こえるところであります。

4年生の後半では割合とか速さとか出てきますよ。

足すとは何か、引くとは何か、かける割るとは何か、それによって何が求められるのか。そういった基本知識がないまま突入すると爆死します。

四則演算が何をしているのか分かっているとスムーズに乗り越えられるこれからの単元。逆に四則演算の意味が分かるまでやらないとグダグダになってしまうこれからの単元。

スムーズとグダグダ、どっちを選びますか？

もちろんスムーズですよね。

だったら、夏休みまであと少し。組分けの点数にこだわるよりも夏休みまでに四則演算の意味を徹底的に叩き込むほうが絶対に合理的ですよ。

これから先の長い2年間を有益に過ごしたいのだったら。

ってか、月に1回とか何の拷問なんですかね、組分けテスト。

テストの点数で一喜一憂するより、自分の子供が何を学び、何を見落としているのか、そんな観点で見ている親なんて殆どいないんだろうなぁと思いつつ、鶴と亀を鍋で煮る梅雨の日の夕刻。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介