【中学受験】予習シリーズ算数5年上　第6回「食塩水（濃さ）」の極意と面積図

食塩水の濃度を求める問題を解けるようになったところで日常生活にはちっとも役立ちません。

少なくとも私はこの30年、食塩水の濃度を気にした試しがございません。

パスタゆでるときも湯にいい感じの量の塩を入れるだけであります。一度も計ったことがありません。

ところが、中学受験では30年以上前から食塩水の問題がなぜか出てまいります。

ホウ酸水でもいいと思うんですが食塩水です。このあたりを疑問に思ってしまっては負けです。負け組です。

気にしないで水に塩を溶かしましょう。

さて、食塩水の問題は割合の問題が基礎になっております。

ですので割合が分からないと解けません。

割合の基礎は小学4年生の予習シリーズ算数下　第6回で学習します。

もし小学5年生の予習シリーズ上第6回「食塩水（濃さ）」の問題が分からなければ小学4年生予習シリーズ算数下　第6回まで戻りましょう。

割合は「もとにする量」「割合」「くらべる量」の3つの要素が出てきました。

1.もとにする量×割合＝くらべる量

2.くらべる量÷もとにする量＝割合

3.くらべる量÷割合＝もとにする量

ですね。

この3要素の理解が食塩水を解く上で前提となります。

で、食塩水ではどうかというとこのようになります。

もとにする量＝食塩水の量

割合＝濃さ

くらべる量＝食塩の量

これを割合の3要素風味に整理してみましょう。

1.食塩水の量（もとにする量）×濃さ（割合）＝食塩の量（くらべる量）

2.食塩の量（くらべる量）÷食塩水の量（もとにする量）＝濃さ（割合）

3.食塩の量（くらべる量）÷濃さ（割合）＝食塩水の量（もとにする量）

このようにあらわせます。

この知識が大前提となってまいります。

割合の3要素がわからないのに食塩水の問題は解けません。食塩水の問題でつまづいているとしたら、おそらく割合でつまづいています。

もしくは割合をあいまいにしてしまっているか、です。

さて、小学5年生の食塩水の問題で絶対に身につけておいて欲しい技能が2つあります。

1つ目は食塩水、濃さ、食塩の3つに問題文を整理すること。

2つ目は1つ目の整理で解けない場合に面積図を書けるようにしておくこと。

この2つです。たった2つ。

この2つを自在に使いこなせると食塩水の問題は余裕です。

なに？予習シリーズには例題が7つくらいあるって？

まさかとは思いますが7つの解き方を全部覚えるわけじゃありませんよね。

7つ覚えたい人は覚えていただくと幸せになるのでしょうが、実は上にあげた2つの技能があれば7つも覚えなくて済みます。

少ないほうがいいでしょ？

ってわけでどうやって整理し、どのような問題に面積図を使うのかを中学受験を経験したことのない親御様でもわかるように説明してまいります。

食塩水の問題の整理方法

食塩水の問題は下のように整理します。

整理します、なんて丁寧な言い方では足りません。

整理しろや！ゴルァ！

これだけです。だまされた気がしますか？だましてませんよ。

食塩水の問題は「食塩水」「濃さ」「食塩」の3つに整理した表を書くのが基本中の基本です。

これをやらない子がどんなに多いか。

食塩水の問題を指導するときは必ずこれを書かせます。

なに？言っても書かない？

普通の子どもは面倒くさがって書かないものです。ですから無理やりにでも書かせるんですよ。

経験則で言いますとほぼこれだけで食塩水に関する悩みは雲散霧消いたします。

では実際にやっていきましょう。

食塩水の問題　基本編

①水80gに食塩20gを溶かすと何％の食塩水になりますか？

②20gの食塩に何gの水を溶かすと10%の食塩水になりますか？

③10%の食塩水200gから水を100g蒸発させると何%の食塩水になりますか？

④10%の食塩水150gから水を何g蒸発させると15%の食塩水になりますか？

⑤5%の食塩水200gに水を何g加えると4%の食塩水になりますか？

上の5つの問題を表に整理しますと下のようになります。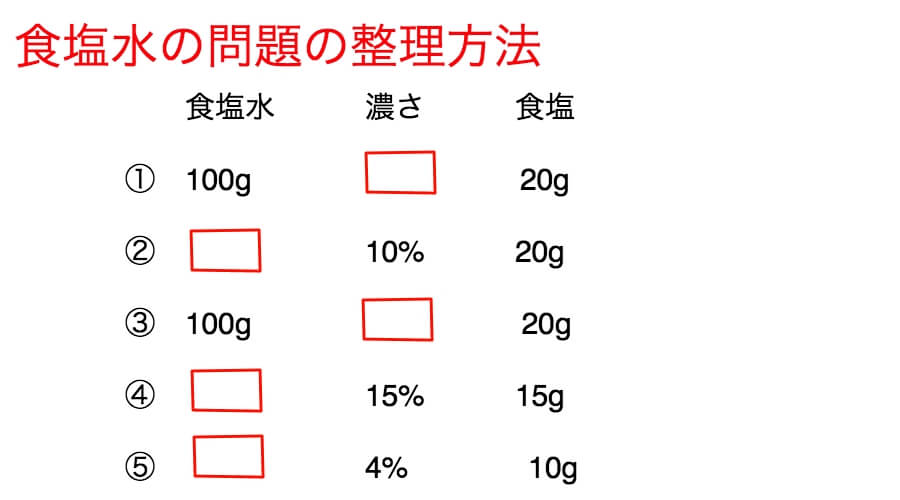

図の赤い□にあてはまる数を求めるだけになりましたね。これは公式を知っていれば簡単にできます。

問題文を整理しますと求めるものが明らかになります。

求めるものを明らかにするのはとても大事な作業です。何を求める問題なのか分からない限り問題は解けませんから。

で、知っておきたい基本知識は下の3つです。

1.食塩水の量は「水の量＋食塩の量」

2.食塩水を蒸発させても食塩の量は変わらず水の量だけが減る

3.食塩水を捨てても濃さは変わらない

あとは問題文を表にあてはめていくだけ。

簡単でしょ？

ちなみに食塩水の公式を使いまして、答えは①20%、②180g、③20%、④50g、⑤50gとなります。

濃さの違う食塩水を混ぜる問題も上の表を使うと解けます。

濃さの違う食塩水を混ぜ合わせる

問題：10%の食塩水150gに5%の食塩水100gをを混ぜると何%の食塩水になりますか？

こういった問題も表を使います。

AとBの食塩水の量、食塩の量を足して食塩水ABの濃さを求める表に整理できますね。

頭の中でやってはいけません。

必ず表に整理します。

ちなみに答えは8%です。

あとは食塩水同士のやりとりをするような問題もあります。

やりとりをし始めると条件はやや複雑になりますが、表にすべて整理していけば解けます。大丈夫。

食塩水のやりとり

問題：濃さが分からない食塩水が100gあります。この食塩水に10%の食塩水300gを溶かしたところ8%の食塩水ができました。100gの食塩水の濃さは何%ですか？

これも整理すると簡単に解けます。

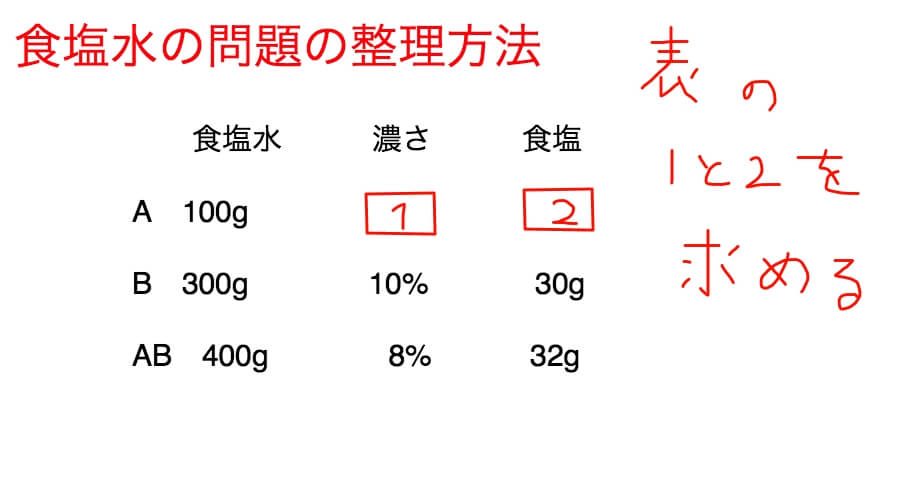
表に整理しますと100gの食塩水の濃さ（1）と食塩の量（2)が分からないことが分かります。

さらっと書きましたが、表に整理すると分からないことが分かるようになるんです。

めちゃくちゃ大事な点です。

算数もしくは数学の問題は何を求める問題で、何が分からないのか整理するのが大事です。

そのためのツールが表なんですね。

ちなみに上の問題ですと、Bの食塩の量は30gでABの食塩の量は32gです。

つまり、Aの食塩の量は2gです。これが□の2に入ります。

したがって、□の1は2%になります。

簡単ですね。

何度でも言いますが、絶対に頭の中でやってはいけません。

必ず表を書く。書くクセを身につける。

これが食塩水の問題を解けるようになるための奥義中の奥義です。

では次は面積図を使う問題にいきます。

1 2 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介