【中学受験】場合の数　ならべ方（順列）と組み合わせの違い・公式の意味・問題演習

いろいろな場合の数の問題

マス目の問題　和の法則

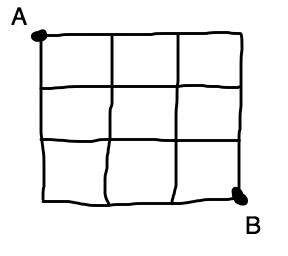
マス目の問題は↓です。

AからBまで遠回りしないときに道順が何通りあるか、といった問題です。

予習シリーズにも解き方がありますのでササッといきますよ。

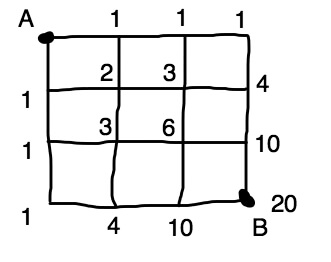
作法としては、

・1通りのところにすべて1と書き込んでいきます。

・次に線の交わるところは数字を足していきます。

・以上

です。

真ん中あたりに必ず通る地点があるパターンもあります。

A地点からB地点まで行くのに必ず乙地点を通るとします。

すると↓こうなります。

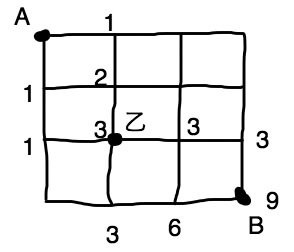
9通りです。

別解としてはA地点から乙地点までの道順を求めて、乙地点からB地点までの道順を求め、その二つの道順を掛けても答えがでます。

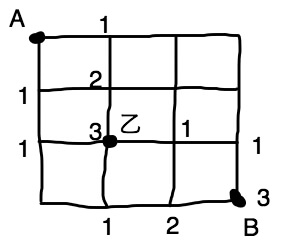
Aから乙までの道順は3通り。乙からBまでの道順は3通り。

これを掛けまして、3×3＝9通り　になりますね。

和の法則と積の法則を使う方法です。

こっちのほうがすっきりするかもしれません。

玉ねぎ問題　積の法則

これが玉ねぎ問題です。

A地点からC地点に行くのに何通りありますか？

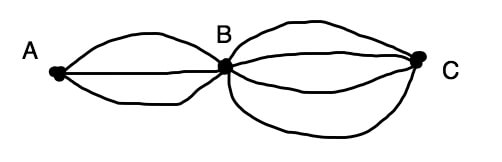
ちなみにこれを玉ねぎ問題と呼んでいるのは多分、私だけです。

一般的には通用しません。

普通はブラジャー問題と呼んだりします。

が、一般的なブラジャーはカップが2つですから、3つ以上カップがある場合どう呼んでいいのか分からない問題が発生します。

お気をつけください。

この問題も玉ねぎに数字を書き入れていきます。

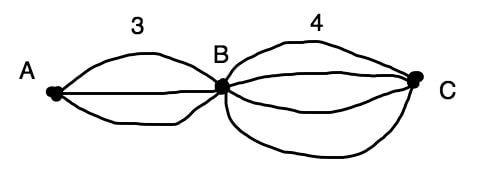
A地点からB地点までは3通り。

B地点からC地点までは4通り。

積の法則を使いまして、

3×4＝12通り　です。

簡単ですね。

これも、通れない地点がある問題とか、徒歩とヒッチハイクとハイヤーから選ぶ問題等バリエーションがありますが、基本は積の法則で解けます。

×地点が通れない場合は、A地点からB地点までが2通り、B地点からC地点までが3通りになります。

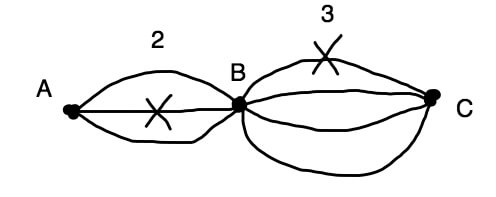
よって、2×3＝6通り　です。

手段が異なる場合もこの考え方で大丈夫です。

塗り分け問題　和の法則・積の法則

塗り分け問題なんてのもあります。

これはやり方を知っといたほうがいいですね。

↓こんな問題です。

下のA、B、C、D、Eを赤、青、黄、緑の四色をすべて使って塗り分ける場合の数は何通りありますか？

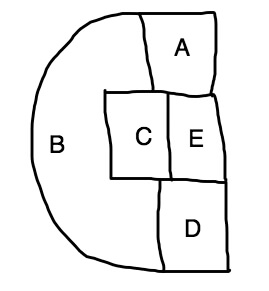
塗り分け問題の場合、まず最初に同じ色で塗れる箇所を探します。

上の図形の場合、A・D、B・Eの2通りあります。

では手順に沿ってやっていきますよ。

手順1　A・Dを赤で塗る場合、B・C・Eは残りの三色で塗りますから3×2×1で6通りになります。（積の法則）

手順2　A・Dを塗る色は赤、青、黄、緑の4パターンありますから、手順1の6通り×4で24通りとなります。（積の法則）

手順3　B・Eを同じ色で塗るパターンも上の手順1、2と同じく24通りあります。

手順4　A・Dの24通りとB・Eの24通りを足して48通りと求められます。（和の法則）

答え　48通り

場合の数　ならべ方（順列）と組み合わせのポイント

長々と書いてきましたが、場合の数「ならべ方（順列）」と「組み合わせ」のポイントは

「ならべ方（順列）」なのか「組み合わせ」なのかを判別する

場合分けをして考える

和の法則、もしくは積の法則、あるいは両方を使う

この3つです。

解き方はいろいろありますが、この3つの基本を理解しておけばそんなに苦労する単元ではありません。

力技で解き方を暗記するのも結構ですが、1ヶ月もすれば忘れてしまいます。

月ごとのテストでいい点数とれりゃいい！

とにかくやり方を暗記するのだ！

といった殺伐としたご意見もあろうかと思います。

分からなくもないですが、どうせだったらいい点数も取りつつ、理解もするほうがいいんじゃないですかね。

短期目線になると目的がすり替わって、心身ともにすり減りますよ。

「いや、別に複雑じゃないよ。むしろごく簡単なんだ。もちろん徐々にやらなくちゃならない。だけど下らないすり切れのためにさんざん時間を無駄にしているんだ」

引用）ボリス・ヴィアン「日々の泡」より

< 前へ 1 2 3

あわせて読みたい

最新のホカホカ記事

書いている人の紹介