【中学受験】場合の数　ならべ方（順列）と組み合わせの違い・公式の意味・問題演習

ならべ方（順列）と組み合わせの判別は大事

冒頭申し上げましたように、高校の数AでPとCは習うはずなんです。

普通に考えるとPとCくらい判別できるはずなんです。

ところが、高校生の面倒を見ていると、びっくりするくらいPとCの判別ができないんですね。

マジでびっくりします。

飲んでたコーラを吹き出すくらいPとCの使い方が分からない生徒が多数です。

そういう子たちに委員長と副委員長の話をすると、

「あぁー！そういうことか！」

と、めちゃくちゃ納得されるんです。

おいおいおい、マジで何教えてるんだYO、高校。

と、昔の私は思ってました。

こういった現象は中学受験塾でも起きます。

公式？解き方？道順？

その前に教えることあるだろうが、と私は思うわけです。

原理を知らないのに方法だけは知っている、なんてやっぱ不健全ですよ。

女の子の気持ちを考えようともしないのに、「おだてりゃ女は喜ぶんだよ！」なんて言ってる男子は不健全だと思うわけです。

まぁ、実際はおだてると女の子は喜ぶんですがね。

方法だけ教え込まれると「これでいける！」と思うようになります。

要するに子どもたちは解き方を覚えりゃどうにかなると高をくくるようになります。

そりゃ、公式やら解き方やらをバンバン教え込まれたらそうなりますよ。

私は公式やら解き方ではなく、どうしてそうなるかといった原理、つまり基本を大事にしてもらいたいと思ってます。

だから、ならべ方（順列）と組み合わせの違いをしつこいくらいお話ししてまいりました。

では、ここからはまた実際的な話にいきたいと思います。

和の法則、積の法則です。

場合の数　和の法則・積の法則

和の法則と積の法則はそれぞれ別で考えると分からなくなります。

ですのでどんなふうに違うのかを並べて考えます。

・和の法則の問題：2個のサイコロを1回振って、出た目の合計が3の倍数となる場合は何通りありますか？

・積の法則の問題：2個のサイコロを2回振って、最初に出た目の合計が3の倍数、次に出た目の合計が5の倍数となる場合は何通りありますか？

「なるほど！サイコロを1回振るか、2回振るかだな！」

いえ、ちょっと違います。

和の法則の問題を解いてみましょう。

・和の法則の問題：2個のサイコロを1回振って、出た目の合計が3の倍数となる場合は何通りありますか？

この場合、2個のサイコロの目の合計は「3」「6」「9」「12」の4通りあります。

それぞれ見ていきますよ。↓のような場合分けも大事ですよ。

「3」・・・「1、2」

「6」・・・「1、5」「2、4」「3、3」

「9」・・・「3、6」「4、5」

「12」・・・「6、6」

全部の場合の数を足して答えは7通りとなります。

ちなみに、この2個のサイコロは区別がないので「組み合わせ」です。

2個のサイコロの大きさや色や形が違う場合は「ならべ方（順列）」です。区別できるからです。

では、次に積の法則にいってみましょう。

・積の法則の問題：2個のサイコロを2回振って、最初に出た目の合計が3の倍数、次に出た目の合計が5の倍数となる場合は何通りありますか？

サイコロを1回振って3の倍数になるのは7通りでしたね。

2回目に5の倍数となるのは「5」「10」の2通りありますね。

では3の倍数と同じように見ていきましょう。

「5」・・・「1、4」「2、3」

「10」・・・「4、6」「5、5」

5の倍数は4通りです。

ここまでは和の法則です。

んで、最後に積の法則を使います。

1回目の7通りと2回目の4通りをかけて28通りが答えです。

さて、和の法則と積の法則、何がちがいました？

和の法則と積の法則の違い

もう一度、和の法則と積の法則の問題を並べてみましょう。

・和の法則の問題：2個のサイコロを1回振って、出た目の合計が3の倍数となる場合は何通りありますか？

・積の法則の問題：2個のサイコロを2回振って、最初に出た目の合計が3の倍数、次に出た目の合計が5の倍数となる場合は何通りありますか？

結論から言いますと、和の法則はそれぞれの場合が独立しているとき、積の法則はそれぞれの場合が関連しているときに成立します。

なお、数学の教科書には和の法則は「同時に起きない場合」、積の法則は「同時に起きる場合」と書いてますがいまいち私にはピンときません。

さて、和の法則の問題では「3」「6」「9」「12」の4通りの目の合計があると申し上げました。

では、たとえば合計が「3」になる場合と「6」になる場合に何か関連性はありますかね？

ありませんよね。独立してます。

逆に積の法則では1回目が「3の倍数」で2回目が「5の倍数」になる場合といったように条件づけがあって関連してますよね。

では例をあげていきます。

和の法則の例

・10円玉を3回投げて裏が2回以上出る場合の数

・2個のサイコロを投げて合計の目が9以上になる場合の数

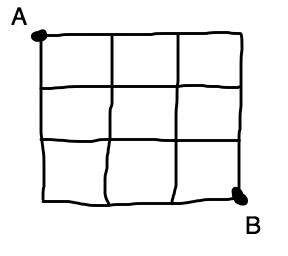
・A地点からB地点までの道がマス目になっている場合の道順の数

※↓こんなやつ

積の法則の例

・10円玉と100円玉を3回投げて、10円玉、100円玉がそれぞれ2回以上裏になる場合の数

・2個のサイコロを2回投げて、2回とも目の合計が9以上になる場合の数

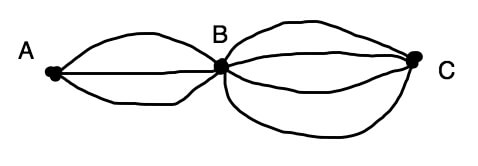
・A地点からB地点を通ってC地点に行くまでの道順の数

※↓こんなやつ（私は「玉ねぎ問題」と呼んでます）

和の法則は独立して起きる現象

積の法則は関連して起きる現象

と覚えておくといいです。

ま、このへんは問題を解いていって感覚で覚えちゃっても問題ございません。

ただ、子どもによってはちゃんと定義を知ってからでないと理解できない子もいます。

理解の仕方は人それぞれ違います。

塾の説明の仕方が合わない子もいます。

結果、成績が振るわなくて、「うちの子、頭悪いのかしら」と心配に思われるかもしれません。

これ、頭の善し悪しじゃなくてその子の理解の仕方と塾の説明の仕方が合ってないんですよね。

ご安心ください。

そういう子にはちょいとカスタマイズして教えてあげるといいと思いますよ。

では、最後にマス目の問題、玉ねぎ問題、塗り分け問題を解いていきます。

え？他にもいろんな場合の数の問題があるだろって？

いえいえ、場合の数の問題は「ならべ方（順列）」なのか「組み合わせ」なのか判別し、

場合分けをしてから「和の法則」あるいは「積の法則」を使えばほぼ解けますよ。

マス目の問題（和の法則）、玉ねぎ問題（積の法則）、塗り分け問題（和の法則＆積の法則）は解き方のテクニックがありますのでちょいと説明をしようと思いまして。

< 前へ 1 2 3 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介