開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問１（２）集合あるいは数の規則性ー第1回

必要とされるスキル

開成中学校の入試問題のうち算数に絞り、これから数十回にわたって様々な問題の解き方と解き方から導出される学習方法について解説をしていきたいと思います。

開成中学校というと中学入試の世界では最難関の一つと言われる学校であり、そのイメージから入試問題においても難しい問題が出題されると考える方は多いかもしれませんが、実際のところは難解な計算や頭を悩ませるような複雑な式を使う必要はなく、極めてシンプルで容易に解くことができます。

必要とされるスキルは大きく分けて2つ、１．何が問われているのかに気づくスキル（問題特定能力）、２．正確に解法を想起し解法に従って解くスキル（問題処理能力）の2つです。とくに１のスキルが重要と考えます。

効果的な学習（狙った部位に効かせる学習）と課題発見（自身の鍛える部位の特定）のために上記の2つのスキルを更に分解していこうと思います。

必要な能力を細分化する

１．問題特定能力

step1　問題文で与えられている条件を整理すること、そして条件を自ら作り出すこと

step2　解答に至るまでの方向性を決めること

step3　方向性をもとに解答までの具体的な道筋を決めること

２．問題処理能力

step4　具体的な道筋に沿った数式を立てること

step5　計算すること

という5つの能力が備わっていれば容易に解ける問題である、というのがここ10年程の過去問を解いて得た感触です。

とくに１の問題特定能力が重要です。これは開成中学校の算数の問題に限らず他の中学校でも同様です。なぜならば何の設問で何について問われているのか分からなければ解法も特定できませんし、計算すらできません。それができなければ解答に至るのは不可能だからです。

当然ですが問われていることを解決するまでの道筋がわからないのに答えはわかりません。

上記のように解くまでのプロセスを分解し明確化しておかないと何が弱く、何を重点的に鍛えるのかが曖昧な状態で勉強を進めることになります。

本当は問題文で与えられた条件が不明確なこと（step1）が算数が苦手な理由にもかかわらず計算演習（step5）をやる、とか、解法や数式を知らない（step4）から解けないのにひたすら応用問題を解く（step1～5の複合）とか、といったように目的と手段が乖離するという事態が出来します。

これでは算数ができるようになるはずがありません。

開成中学校でとくに求められるスキル

求められるという意味では全部ですが、条件を整理・発見し、方向性を導く、この2つを除けば並の学習レベルで解くことができ、この2つが他校よりも圧倒的に難しいです。とくに条件を発見する能力が重要です。隠れた条件を発見しないと解けない問題が多いからです。

逆に言えばこれができる子を求めていると言えるかと思います。もう少し詳しく言うと「複雑に見える問題の隠れた前提条件を見つけ、シンプルに方向性を導き解答まで導けるように設計できる子」ということになるのだと思います。

けして計算が早い子とか複雑な計算をこなせる子というわけではないです。

実際の問題を解く

平成29年度の大問１の（２）の問題を解いていきます。

１から２０１７までの整数のうち、３でも４でも割り切れないものを考えます。そのうち、２の倍数と５の倍数はそれぞれ何個ありますか。

step1　条件を整理、発見する

１から２０１７までの整数のうち

「２０１７までの整数で」という条件です。

３でも４でも割り切れないもの

「２０１７までの整数」のうち「３の倍数でも、4の倍数でもない整数」という条件です。

そのうち

「２０１７までの整数のうち」という意味です。

2の倍数と5の倍数はそれぞれ何個ありますか？

これはそのままの意味です。すなわち与えられた条件をつなげてみると、「2017までの整数で3の倍数でも4の倍数でもない、2の倍数、そして5の倍数」ということになります。

step2　解答の方向性を決める

これは集合の問題だとこの時点で気づきます。

「2017までの整数で3の倍数でも4の倍数でもない、2の倍数の数」

と、

「2017までの整数で3の倍数でも4の倍数でもない、5の倍数の数」

ということだからです。

step3　解答の道筋を決める

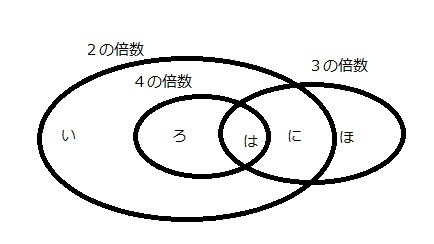
１．「２０１７までの2の倍数の個数から3の倍数と4の倍数を除く」

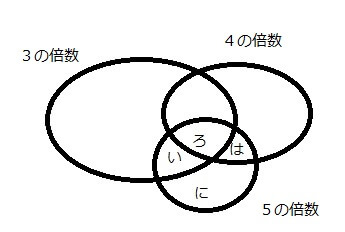
２．「２０１７までの５の倍数の個数から３の倍数と４の倍数を除く」

という二つのベン図を描きます。

１．「２０１７までの2の倍数の個数から3の倍数と4の倍数を除く」

２．「２０１７までの５の倍数の個数から３の倍数と４の倍数を除く」

step4　数式を立てる

集合の問題であればベン図を使用すれば殆どの問題は解けますので、集合の問題＝ベン図と機械的に考えてしまっても大きな問題はありません。

１．「２０１７までの2の倍数の個数から3の倍数と4の倍数を除く」

２の倍数の総数から上記の「ろ」「は」「に」を引いた「い」が正解となります。

すなわち、

２の倍数の数・・・２０１７÷２＝１００８・・・１

は・・・２０１７÷１２＝１６８・・・１

ろ・・・２０１７÷４－１６８（は）＝３３６・・・１

に・・・２０１７÷６－１６８＝１６８

で、１００８－１６８－３３６－１６８が「い」となります。

２．「２０１７までの５の倍数の個数から３の倍数と４の倍数を除く」

５の倍数の総数から「い」「ろ」「は」を引いた「に」が正解となります。

すなわち、

５の倍数の数・・・４０３・・・２

ろ・・・２０１７÷６０＝３３・・・３７

は・・・２０１７÷２０－３３（ろ）＝６７・・・１７

い・・・２０１７÷１５－３３（ろ）＝１０１・・・７

で、４０３－３３－６７－１０１が「に」となります。

step５　計算する

２の倍数の問題の方の「い」は、１００８－１６８－３３６－１６８＝３３６

答えは３３６となります。

５の倍数の問題の方の「に」は、４０３－３３－６７－１０１＝２０２

答えは２０２個です。

最後に

集合の問題であればベン図を用いればほぼ外れがありませんので、機械的に解答への道筋を決めることができ、数式を立てられますので他の解き方よりも速く解答を導くことができます。上の計算ですと煩雑に見えますが、実際は慣れてしまえばなんということはありません。

ではまた次回ということで。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介