開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問３（２）相似の図形ー第3回

stepを６つに区切って問題を解くことの意義とは

今日は開成中学校平成29年度入試問題「算数」の大問３の（２）を解いていきたいと思います。

では実際の問題に入る前にstepを５つに分けて問題を解くことの意義について話をしていきます。大きく分けて３つの理由（意義）があって５つに区切って解くことを推奨しています。

１．解答を導く段階を分割し何をするのか明確にすること=思考の明確化

２．解答に至るまでの段階のどこで行き詰ったのかが分かり引き返すことができる＝可逆性

３．行き詰った箇所を特定し学習に役立てられること＝検証性

上記の３つです。少し説明を加えたいと思います。

まず１については、今何をしているのか明確にすることによって漫然と解くのではなく集中して解けるようにするという意味があります。

また、常に同じ方法で解答を導く癖をつけて「この解き方だったらどんな問題がきても大丈夫」と自信を持てるという効果があります。

同じ方法で常に解き、その同じ方法であれば解けるという自信を持つことで未知の問題が出てきたり、極限的な状況においても心理的に落ち着くことができるのです。

また、同じ方法で解くことでその方法論における習熟度が次第に高まります。

ある方法を使いこなすためには「練習」がやはり必要です。「練習」というのはある動作や解き方を反復することによって、その動作や解き方がレベルアップすることを期待して行うものです。

そしてそのためには同じ動作や同じ解き方を反復しなければなりません。

それが「練習」というものです。

解法を分解してstep化し、反復練習することにより個々のstepそれぞれの習熟度を高めることができ、またstep化して順を追って解く方法についても習熟度を増すことができます。

次に２についてはたとえばstep２で何が問題解決のための方向性が見えたものの、step３、step４と進む段階で解けないことに気づいたときにどこまで戻って思考をやり直すのかが分かるという意味です。

step２までいったもののうまくその先に進めなかった場合、step２で間違えた方向性を示していたのか、あるいはstep１で条件を整理しきれなかったのか、どちらかに問題が発生したいたと見定め、そのstepまで戻ることができるということです。

難関校の問題においてはきれいにstep１～５までを辿るのではなく、誤った方法を選択したがゆえに解けずまたやり直すようなことが発生します。段階を区切っておくとどの段階まで戻れば良いのかが分かりやすくなります。

最後に３は、それぞれのstepのどこで間違えたのか、どこをクリアできなかったのかを分析・検証し、

ここを間違えた（クリアできなかった）から解けなかった

あるいは

ここが弱点である

ということが可視化されるメリットがあります。可視化された問題点や課題点をもとにそれを学習に役立てることができます。

それぞれのどのstepで間違え（クリアできず）、どのstepで間違え（クリアできない）やすいのかを特定し学習計画を立てるのです。

しっかり条件を整理する訓練、隠された条件を発見する訓練、与えられた条件から方向性を導き出す訓練、導き出した方向性から具体的な道筋を設計する訓練、具体的な道筋から数式を立てる訓練、・・・etc

学習というのはむやみに行っても効果はありません。きちんと効かせたい箇所に効かせるように行う方が効果があります。つまり、ポイントを絞った学習アプローチの方が課題である箇所に対してピンポイントで学習でき効果が期待できるのです。

私が小学生のときにやっていた勉強法ですが、単純にある問題が間違っていたから同ジャンルの問題を解くというのでは効率性に欠けると考えています。

勉強が足りないのではない、考えが足りないのである

また私の話で恐縮ですが、私が中学校受験を志していた時の勉強方法はひどいものでした。

塾では解法ごとに単元が分かれています。「つるかめ算」の回、とか。

そしてまずは塾に行き、先生の話を聞きます。次に先生の話に沿った練習問題を解きます。練習問題を解いたところで基本演習の問題を解きます。それから応用問題を解きます。

私は基本演習までは解けましたが、応用問題になったときにはからっきしでした。

そこで家に帰ってから応用問題を解く練習をします。ところがうまく解けないので解答を見ます。解答を見ると何となく分かった気になります。分かった気にはなるのですが、他の応用問題はまたやはり解けません。解けないので解答を見ます。何となく分かったときになります。、、、以下繰り返し。

今から過去の自分にアドバイスするならば、

「解けた解けなかったという結果ではなく、どの段階で間違えた（クリアできなかった）かを特定して、自らの課題や弱みをまずは把握しましょう」

と言うと思います。では過去の私は何につまづいていたのでしょうか？

それはずばり、解くためのロジックを確立（解法の設計）ができていないにも拘わらず、覚えた解法を当てはめて解こうとしていたからだと考えています。

ロジックを確立（解法の設計）をするのはstep３の能力です。そして真の問題点はstep１で問題文を咀嚼できていない、そして咀嚼できていないからこそ解答を導くための方向性を導けていない点にあります。

「つるかめ算」の回であれば「つるかめ算」で解ける問題が並んでいるのは自明の理ですから、解法はすでに特定できているわけです。ところが、「つるかめ算」をどのように使用するのかが見えていない状態で、「つるかめ算」を無理に使おうとするので解けないという現象が発生するのです。

これを防ぐためにはstep１やstep２できちんと問題文を理解、把握し、step３につなげるというプロセスが不可欠です。

ここができていなかった、と振り返ってみて思います。

頭の良い人は笑うかもしれません。でも私のような凡人はそうなのです。基本問題は解けても応用問題は解けない理由はそこにあります。

しかし、凡人であれ正しい考え方のもと行う正しい訓練により解けるようになります。絶対に。

では問題演習にうつりましょう。

step1　条件を整理、発見する

開成中学校平成29年度算数大問３の（２）です。与えられた条件は、下記の問題文の太字部分ですが、それをもとに新たな条件を求めることができます。

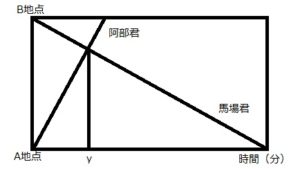
A地点とB地点の間に一本道があります。阿部君はこの道をA地点からB地点へ向かって分速50mで進みます。馬場君もこの道をB地点からA地点へ向かって一定の速さで進みます。二人は同時に出発し、B地点から250m離れた時点ですれ違いました。また、阿部君がB地点に着いてから46分12秒後に、馬場君はA地点に着きました。右の図（ここでは下の図）は、二人が出発してからの時間とA地点からの道のりの関係を表しています。二人が出発してからすれ違うまでにかかった時間をy分とするとき、yの値を求めなさい。

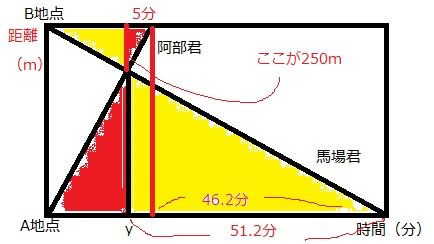
二人は同時に出発し、B地点から250m離れた時点

つまり、阿部君は二人が出会った地点からB地点まで5分で移動しています。

なぜなら阿部君は分速50mで進んでいるからです。

B地点に着いてから46分12秒後に、馬場君はA地点に着きました

阿部君がB地点にたどり着いてから馬場君は46分12秒後にA地点に着いています。

46分12秒後というのが嫌なので46.2分後とします。

また二人が出会った地点から阿部君がB地点まで5分で移動していますがので二人が出会った地点から馬場君がA地点に辿り着いたのは51.2分後（46.2＋5）です。

step2　解答の方向性を決める

上では問題の条件を整理し、隠れた条件を洗い出しました。

次にこの整理した条件を図に表してみます。赤い部分が後から加えたり、改変した部分です。

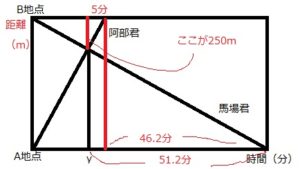
はい、こんな感じです。

ここから見えてくるのは相似の図形である、ということと相似比によって解けそうだということです。

step3　解答の道筋を決める

これは、「旅人算のダイヤグラム変換⇒相似比」の問題です。

旅人算は受験生であれば誰でもやったことがあると思います。ところが単純な旅人算ではたいていの入試問題は解けません。そこで役に立つのがダイヤグラム変換の技術です。

ダイヤグラムに変換することによって、相似の図形を作り、その相似比によって解くことができる利点があるのと、また図形化することで視覚的に解くことができるのでおすすめです。

旅人算は常にダイヤグラムに変換するように練習しましょう。

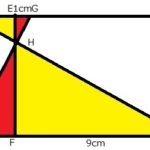
なお、この問題では、以下のように黄色の図形同士と赤色の図形同士の相似比に着目して解くことにします。

step4　数式を立てる

黄色の図形の相似比はy（分）：51.2（分）です。

赤色の図形の相似比は5（分）：y（分）です。

両三角形とも縦の辺が共通ですので、y：51.2＝５：yが成り立ちます。

step5　計算する

比の外項と内項の積は等しくなりますので、

y×y＝51.2×5

こちらを計算しますと、

y×y＝256

となり、

256は16の二乗なのでy=16となります。

答えはy=16です。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介