開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問4（３）図形ー第6回

いきなり解こうとしない

ちょっとひねった問題を解こうとするとき、もしかしたら何となく自分の知っている解法を当てはめようとしたり、あてずっぽうで計算をし始めたりはしていないでしょうか？

もしかしたらそれで解けることもあるかもしれません。

ただし、それはその程度で解ける問題だったからに他なりません。あるいはたまたまです。そのような解き方の癖は早く克服してしまいましょう。開成中学校をはじめとした難関校の問題はそれでは安定的に解くことはできません。断言します。

同様に閃きに頼ったりするのも止めましょう。それはギャンブルと変わりがありません。一度しかない試験の場で閃かなかったらそれでおしまいです。

かくいう私自身も小学生の頃はそのようにして問題にあたっていました。何となく図形に線を引っ張ってみたり、何となく比の問題なんじゃないかと思って必死に当てはめようとしたり、あるいはいきなり計算を始めたり。

ちょっとした問題であればその方法でも解けました。

が、本当に練りこまれた問題はその方法では解けませんでした。しかしたまにその方法で解けてしまう。この少ない成功体験が足を引っ張っていました。ちょっと解けたという経験によって、誤った思考、すなわちこのやり方でいいんだという思考に陥ってしまっていたのです。

結果として解答に至る道がギャンブルとなり果てました。

ギャンブルというのは再現性がありません。そこに辿り着くための道筋が明確になっていないからです。一度やったことを二度やれと言われてもできないのです。

私が冒頭で閃きに頼らないと言ったのは、閃きというのは道筋が明らかではない＝再現性がない＝安定して問題を解くことができない、からです。

再現性のある方法というのは道筋が明確であること、つまり論理的に追跡可能で検証可能である方法のことです。

閃きは偶発的ですが、論理の積み重ねは何度でも行うことができます。志望校の問題を解くにあたり安定して良い点数をとるために再現性のある論理的な手法で解く必要があると考えるのはこれが理由です。

だから何度も言いますが、自分なりの解答ロジックを持つことが大事なのです。

私がstep1～5までを踏んで解く方法を推奨するのは、私なりに編み出したこの方法で8割がた問題を解けるという確信を得ているからです。

では本日の問題に入りたいと思います。

step1　条件を整理、発見する

図2の「あ」の長さは何cmですか。

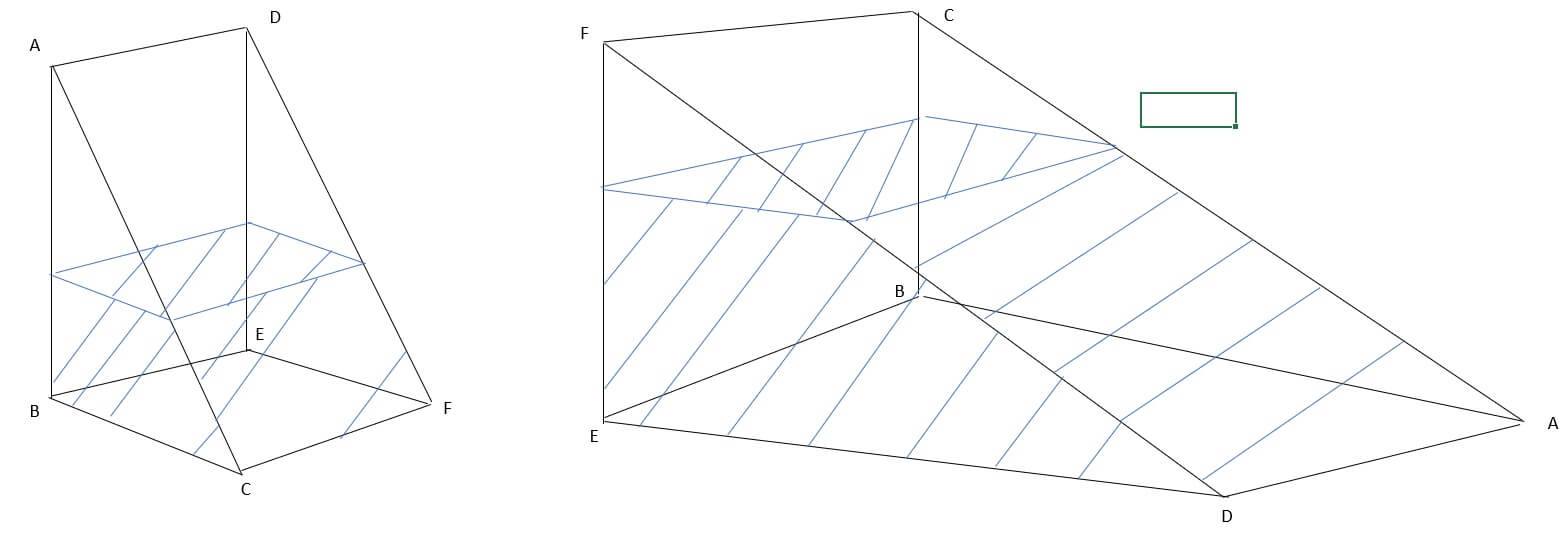
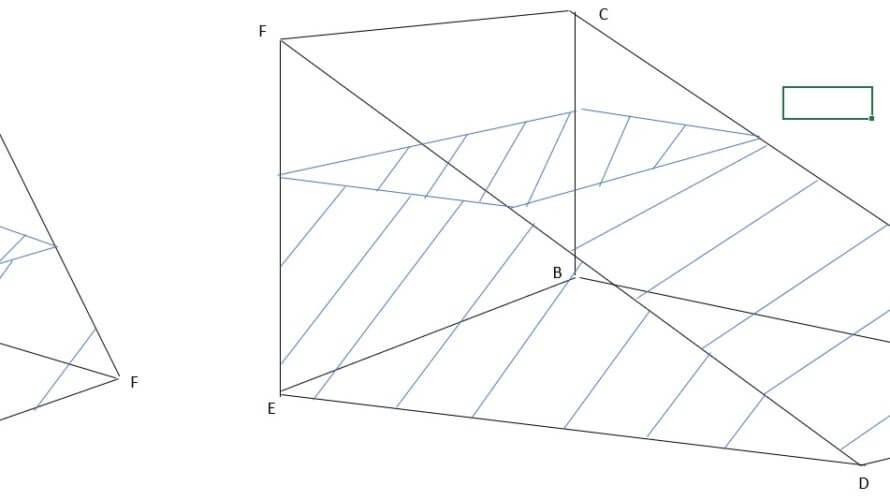
では、立体図からいきましょう。

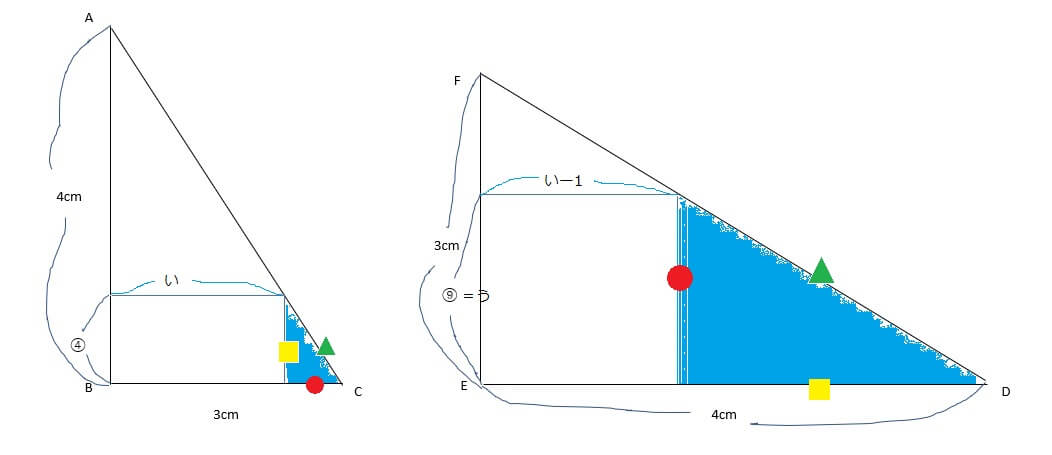
では次に平面図にしてみましょう。（１）、（２）の問題で分かったことや、もともと与えられている数値、記号を書き込みます。前回も申し上げましたが、図形を解くには分かる限りの数値（条件）を書き込むことが大事です。

ここから分かるのは、水色部分は相似の図形で、対応する相似の辺は赤丸、四角黄、緑三角ということです。なぜ相似と分かるのか。立体図を見てみてください。

左の図の水色部分ははABCの三角形と相似であることがすぐにわかると思いますし、右の図のDEFはABCと同じですね。つまり、水色部分はABCと相似です。したがいまして、水色部分は相似の関係にあることが分かります。

赤丸（３）：黄丸（４）：緑三角（５）という相似比を見出すことができます。

対応する辺はわかりやすく図形で色分けしてみました。色分けは試験中できないかもしれませんが、図形で対応する辺を表すのは試験中でもできます。とても分かりやすくなりますのでお勧めです。

step2で読み解いて欲しいのは相似な図形がある、ということです。

step２　解答の方向性を決める

相似の図形の相似比から「あ」（図１の④にあたる辺）を求める問題であることと当たりをつけることができます。では相似の図形と相似比の性質を使って解いていきましょう。

step３　解答の道筋を決める

図１の「い」の長さは「３ｃｍ－赤丸」です。図１の赤丸は④×3/4で③と求めることができます。

図２の「え」（「い」－１）の長さは４ｃｍ－黄丸です。図２の黄丸は⑨×4/3で⑫と求めることができます。

「え」は「い」よりも１ｃｍ短いです。

さてこれを等式にしてみましょう。

step４　数式を立てる

3cmー③－１cm＝4cmー⑫

上の式の＝の左側で1cmを引いているのは右の図の上底より左の図の上底が1cm短いので等式にするためには1cm引く必要があるからです。（＝の右側に1cmを足しても同じ結果になります）

step５　計算する

この等式は以下のようになります。

⑫－③＝４ｃｍ－３ｃｍ＋１ｃｍ

⑨＝２ｃｍ

上の等式が導かれるのは、

ー⑫を左の式に移動すると＋⑫になり、⑫－③で⑨、左の式の3cm－1cm＝2cmを右の式に移動すると、4cmー2cm=2cmとなるからです。

⑨＝2cmなので①は2/9cmとなります。この問題の「あ」は④なので、④×2/9cm＝8/9cm。

答えは8/9cmとなります。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介