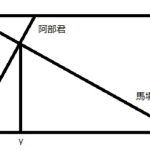
開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問３（１）相似の図形ー第2回

開成中学校の算数の問題における傾向

ここ10年程の算数の問題に限ってという言い方しかできませんが、非常に図形の問題が多いという印象があります。多いどころか毎年必ず出題されると言っても過言ではありません。

したがって開成中学校の算数対策としては図形の演習は必須です。

では、なぜ図形なのかといえば、推測となりますが図形は最も発想の柔軟性が求められるからだと考えています。すなわち、出題される図形の問題の「何か」に気づければ解けますし、気づかなければ解けない、果たして受験生諸君は気づけるのか？という挑戦を投げかけているように思います。

第１回目において、私は「開成中学校の問題は気づけば解ける」と言いましたが裏を返せば気づかなければ解けません。図形の問題は気づける子供なのか、気づけない子供なのかを判別するためにはうってつけです。

気づくという言葉は抽象的な言葉なので分かりにくいと思いますので言い換えます。

問われていることを特定する能力のことです。

ただし、図形においては相似の問題ということには気づけても、どうすれば相似の図形として解くことができるのか、どうすれば解答を導くことのできる相似の図形を想起できるのか、ここがポイントとなります。すなわち条件の整理と隠れた条件の発見です。

すなわち線を引けば相似の図形が浮かび上がるけれどもどう線を引くか、もしくは相似の性質を利用してどことどこの比が分かれば問題が解けるか特定するか、そういった類の問題です。

今回解く平成２９年度大問３の（１）は線を引くことはありませんが、解答を導くためには相似の図形の概念と何が分かれば問題が解けるのかという発想力が問われています。

では問題の解法に移ります。

step1-3　条件を整理し相似の問題であると当たりをつける

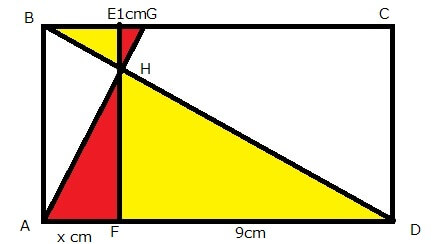
右の図において（このブログでは下の図）、四角形ABCDと四角形ABEFはどちらも長方形で、３つの直線AG、BD、EFが１点Hで交わっています。GEの長さが１ｃｍ、DFの長さが９ｃｍ、AFの長さがxｃｍのとき、xの値を求めなさい。

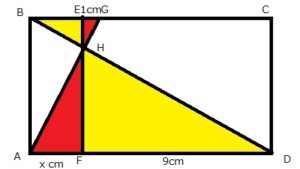
上記のとおり、赤で塗りつぶした図形と黄色で塗りつぶした図形が相似であると、step2までの段階で理解します。なぜなら、四角形ABCDは長方形であり、直線がHを交点として平行な辺BC、ADに到達しているからです。

すると、三角形AFHとGEHが相似であり、三角形BEHとDFHが相似であることを理解することができます。

平行な辺を見つければ何かしらの相似は見つけることができます。

そしてこの問題はxの値を求める問題ですので、問題の手がかりの少なさからして相似の問題の可能性が最も高いと当たりをつけます。

step4　数式を立てる

相似の図形は対応する辺と辺の長さの比が同じであり、対応する角の角度が同じであるという性質を持ちます。

今回問われているのは長さですから、以下の辺と辺の比を求めればxはわかるはずです。なぜならば、GEの１ｃｍとAF（＝ｘ）が対応しているからです。

▼黄色の図形

BE：FD、EH：FH、DH：BH　この３組の辺の比は同じです。

▼赤の図形

AF：GE、FH：EH、AH：GH この３組の辺の比は同じです。

上記の中で比として表せるのは、AF:GEでx：1です。xの値が何かはわかりませんが、三角形AFHとGEHの辺の比はx：１となります。

次に比としてあらわせるのがFD：BEで９：xとなります。三角形AFHとGEHの辺の比は９：xでもあるということです。

つまり、AF:GEとFD：BEの辺の比は同じですから、以下が成り立ちます。

x：１＝９：x

そしてここで思い起こして頂きたいのが比例式の外項と内項の積はイコールになるということです。これを思い起こすことができれば簡単に処理することが可能です。

step5　計算する

９となるようなxの二乗を求める、という問題に収れんされ、答えは３となります。

つまり、内項は９×１＝９で、外項はx×xだからです。

答えは、

xは３です。

図形は本当に難しい

図形の難しさは発想さえできれば解けるし、発想できなかったら解けない点にあります。様々な問題を解くことも重要ですが、基礎をしっかり理解して利用することができることが最も重要です。

基礎を理解し、基礎から逆算して問題を解くための道筋をつけられれば解けるからです。

であるからして、ある問題を与えられたときに、それが図形の性質の何に充当するのか、何を利用すれば解けるのかを訓練で割り出せるようになって頂きたいと思います。

最後に

図形は本当に難しいのでこれから何回かは図形を中心に解いていきたいと思います。

その中で図形を解くための思考方法を盗み出していただければこれに勝る幸いはございません。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介