開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問4（２）図形ー第5回

気づけば解けるし気づかなければ解けない、その違いは？

気づけば解ける、気づけなければ解けない大問4の(2)はそういう問題です。ただそんなことは受験生が本当に知りたいことではないはずです。本当に知りたいのは、

どうすれば気づけるのか

その1点です。

では、気づくということについて考えていきたいと思います。まず、気づくとはどういう状態のことを言うのでしょうか？いくつか実例を交えながら説明していきたいと思います。

気づきの事例

「お母さんが顔をしかめている。太郎はお母さんが怒っていることに気づいた」

「女の人が泣いている。太郎は女の人が悲しがっていることに気づいた」

「男の人が足を押さえている。太郎は男の人が足を痛めていることに気づいた」

いずれも太郎は人の様子や挙動からその人がどのような心の状態にあるのか気づいています。ではなぜ気づいたのでしょうか？それは人の様子や挙動と定型的な心の状態との結びつきを太郎が経験的に知っていたからです。

つまり、しかめている人＝怒っている、泣いている＝悲しい、体の一部を押さえている＝痛い、という類型的な挙動と心の状態との結びつきを事前に知っていて、それを目の前の現象に応用することができたからです。

気づくということには二つの要素が必要である、ということを知ります。すなわち、定型的な結びつきを知っているということと、それを目の前の事象に当てはめることができる、ということです。

この二つの要素が満たされたときに人は何かに気づくことができます。知識とその応用、と言い換えることもできます。

この問題では、というよりは開成中学校の問題においては基本的な知識を目の前の事象（問題）に当てはめることができる、という能力が解くにあたって必要となります。

基本的な算数の知識は絶対に必要です。私はことさらに問題文を解釈することの重要さを解いてきましたが、それは基本的な算数の知識の習得を否定するものではありません。

しっかり問題文を解釈し、問われていることを平易なかたちに置き換え、そして基本的な算数の知識を当てはめることにより解くことができるのです。

その両輪が解答するにあたって必要なことです。

前置きが長くなりました。問題を解いていきましょう。

step1　条件を整理、発見する

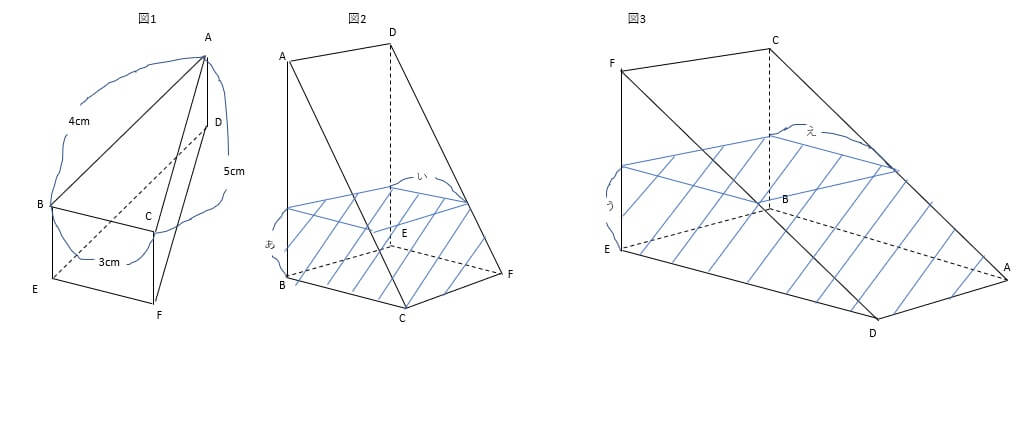
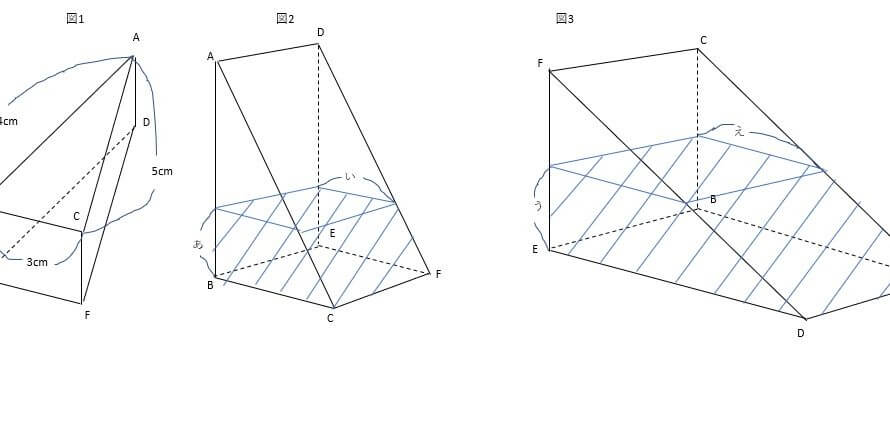
図3の「え」の長さは、図2の「い」の長さより何cm長いですか、または短いですか。解答らんの「長い」、「短い」のいずれかに〇印を付け、その差を答えなさい。

では、図を見ながら条件を洗い出していきましょう。

上は問題に添えられていた図形です。それでは次に第4回目で導きだした図形も呼び出してみましょう。

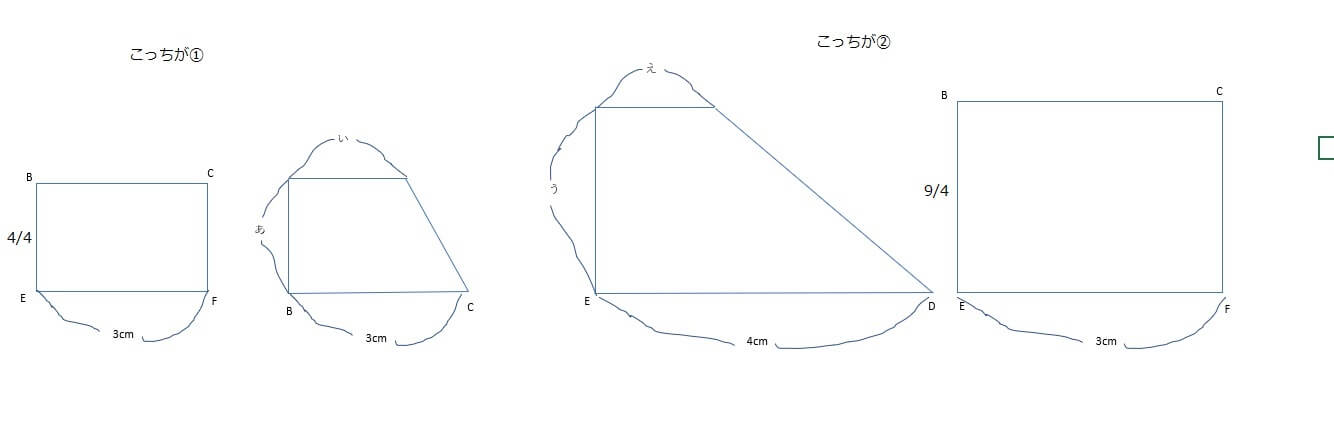
はい、手がかりはこの2つです。ではこの2つの手がかりをもとに考えていきましょう。

まず、問題文の図形の図2と図3ですが、体積は4:9となります。なぜなら、5/4倍に水を追加したから、4:4＋5で4:9となります。

で、図2と図3の水の体積を求めるには「台形の面積×奥行き」となります。奥行きは図2がBEで図3がEBですので、同じ長さです。

したがって台形の面積は4:9です。BEとEBは同じ長さなので、①と置きます。「図2の台形の面積×奥行」×①:「図3の台形の面積×奥行」×①が4:9になるのであれば、「図2の台形の面積」：「図3の台形の面積」は4:9になりますよね。

そして、台形の面積は（上底＋下底）×高さ÷2で求められます。で、この台形の高さは図2が「あ」で、図3が「う」で、(1)で比は4:9と求められましたよね。ということはすなわち（上底＋下底）÷2が図2と図3で同じになるはずです。÷2は両方とも行っていますから、上底＋下底が同じ値になるということです。

図2の台形の高さが④で図3の台形の高さが⑨だとして、これを式にすると、

「？×④：?×⑨＝4:9」である。すなわち、？が同じ数であるときに「図2の台形の面積」：「図3の台形の面積」は4:9で、台形の高さが4:9であるということが成り立ちます。

step2　解答の方向性を決める

①と②の台形の上底＋下底が同じ値になるということに着目してみると簡単に解けそうです。

step3　解答の道筋を決める

①の上底は不明で、下底は3cmです。

②の上底は不明で、下底は4cmです。

で、①と②の台形の上底＋下底が同じ値になるので、

step4　数式を立てる

step3を式にすると、

３＋X＝４＋ｙ

になります。

step5　計算する

ｘ－ｙ＝４－３

と式を変形することができます。

つまり答えは1cm、「え」が「い」より短いということになります。

この問題は難しい解法や、ややこしい計算を持ち出さなくても解釈や内容理解によって十分解くことができる問題です。

気づきとは

さて、何に気づけば解けたのでしょうか？何個気づけば解けたのでしょうか？以下の通りです。

1.体積が4:9である

2.奥行が同じなので台形の面積は4:9である

3.台形の高さが4:9なので（上底＋下底）は同じである

という3つの要素に気づくことができれば解ける問題です。

気づくためには「図形、体積の性質をしっかりと理解している」ことを前提として、それを「目の前の問題に応用する」力が必要です。

知識と応用という言葉にしてみれば凡庸ではありますが、ここをしっかりと学習することがこの問題を解くにあたっては必要となります。

1、2、3のどれかが欠けていたとしたら、基本的な図形の問題を繰り返し解いて図形の性質を覚えることをおすすめします。

もし図形の性質はわかっていたにも拘わらず解けなかったのだとしたら、しっかりとstep1～3までの流れを踏んで解く練習をすることをおすすめします。

自分の弱点を知るには問題にぶちあたり解けないという経験を繰り返しする中で何が苦手なのかを分析するしかありません。そして弱点を克服するには苦手な事項を基本的な知識の習得と、step1～3の練習をする必要があります。

そしてそれが気づく力につながり、結果として問題が解けるということになるのです。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介