開成中学入試問題「算数」を徹底解説、平成29年度「算数」大問１（２）集合の学習を行うー第1回

学習スタイルについて

第１回目を終えることができましたが、受験生にとって本当に重要なのは問題を解くことによって自分自身の弱点を分析し特定することと、得られた課題を克服するために学習することです。

そういった意味では問題を解くことが重要なのではなく、問題を解くことによって課題を特定し、克服することが真に重要なのだと言えます。

「解く→分析する→課題を特定する→課題を克服するための学習方法を計画する→学習計画に則って学習する」

これこそが真の学習スタイルだと考えます。

では振り返ってみましょう。問題を解くにあたって、私は問題の答えにたどり着くために分解し、stepごとに区切って解答を導いていたと思います。では、そのstepの中でどこにつまづいていたのでしょうか？

よく考えてみてください。

わからなければ一度問題を解いてみてください。

計算間違いをしていましたか？（step5でつまづいたのでしょうか？）

⇒であれば計算をしっかり練習しましょう。

解答までの道筋が分からなかったですか？（step3でつまづいたのでしょうか？）

⇒であれば問題を最後まで解かずに解答までの道筋を設計する練習を繰り返しましょう。

あるいはどうやって解いて良いのかわかりませんでしたか？（step4でつまづいたのでしょうか？）

⇒であれば塾のテキストの単元ごとに数式を立てる練習をしましょう。

統計をとったわけではありませんが開成中学校の問題を解いてみて、どう解けばよいのかわからないという方step1～3までの初期の段階でつまづいているものと思います。解答までの道のりを描くことができないのです。そして問題を解けないのです。

そうした方におすすめなのが、問題を最後まで解かずにどのように解けばよいのかを特定する練習をすることです。とくに条件の整理と隠れた条件の発見に力を注いでみてください。ここができないと次には進めません。

開成中学校の問題でなくとも構わないので「どんな道筋をたどれば解答に至るのか」を特定する訓練をしてください。具体的には「これは相似の問題である」「これはつるかめ算の問題である」「これは時計算と規則性の複合問題である」と特定し、解答までの道筋を想起するだけで構いません。

人生は短く、受験勉強は更に短いです。したがって、弱点を補う学習をするにあたってはピンポイントに必要なことだけに絞り学習しなければ、あっという間に２月はやってきます。

集合について

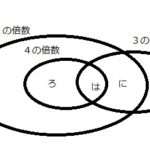
集合という解法において、私はベン図を用いましたがこれは使い方さえ分かれば大変便利で応用のきく解法です。

ベン図を用いるには２つのスキルが必要です。

１．正確にベン図を書けること

２．ベン図から正確に集合の数値を導けること

１、の正確にベン図を書くには論理が必要になります。論理というと一見難しそうですがとても簡単です。

すなわち、「AはBである」「AはBではない」「AはBに含まれる」「AはBに含まれない」という４つが分かればベン図における論理を導けます。

ベン図は書けるということがほぼすべてです。次の演習でベン図を書いて求めてみてください。

１．１０００の整数のうち１１の倍数と１３の倍数を除く整数を求める

２．１０００の整数のうち１１の倍数かつ１３の倍数求める

３．１００の整数のうち２の倍数と５の倍数を除くを除く整数を求める

４．１００の整数のうち２の倍数かつ５の倍数を求める

上記は２つの集合の問題ですが、３つの集合でも考え方は同じです。

これ以外にも自ら考えてベン図を書いてみたり、集合の問題が出てきたときにベン図を書く習慣をつければ、ある問題が集合の問題と特定できればほぼ解けたも同然です。

なぜベン図を推奨するのか

私は大問１の（２）を解くにあたりベン図を使用することを推奨しました。

なぜかというとベン図を書くことができれば視覚的に求めるものが分かり、そして何よりも重要なのが集合の問題であればベン図を使う、と思考を単純化できるからです。

思考の単純化というのはAだったらBである、とか、Aという状況だったらBを利用する、といったように1対1の関係になっていることを指します。

これが大問の（２）を数の規則性を使うとすると、数の規則性における多くの解法から取捨選択する必要が出てきます。

集合ではそういったことはなく、集合＝ベン図と解法の特定がスムーズに行えます。

何度も言いますが、算数の問題、とくに開成中学校の問題はstep1～step3が重要で、かつ難しいポイントです。ですからこの段階で余計なことを考えずに解法を導けるやり方が圧倒的に有利となるのです。

さて、２回目は大問３の（１）を解きます。これは気づくか、気づかないか、それだけの問題です。気づけば小学４年生でも解けますし、気づけなければ大人でも解けません。むしろ解ける大人のほうが少ないのではないかと思いますが。

複雑な問題（＝事象）を解くためには気づきが必要です。

気づけば必ず解けます。

だから気づく練習（つまり特定する能力と、解法を想起する能力）が必要なのです。

あわせて読みたい

最新のホカホカ記事

書いている人の紹介