【中学受験】公文の算数どこまでやるか・いつからやるか　特にやめどきに困るよね

低学年で公文、高学年で中学受験塾への宗旨替えはもはや成功の定説と化してまいりました。

そこで親御さんが悶々とするのがやめどきじゃないですかね。まさに苦悶式。

「一所懸命やってるし、まぁ、H教材くらいまで・・・」

とか、逆に

「C教材までしか進んでないけど4年生だしそろそろ・・・」

みたいな。

結論から言いますと、F教材までで中学受験に役立つ学習は終了いたします。

もちろんやりたければG教材、H教材までやっていただいても困ることはございません。

が、中学受験に役立つ、言い方を変えますと中学受験に出てくる計算はF教材まででございます。

だって、G教材に入るとマイナスの概念とか、100本ノックのような文字式の計算をするんですよ。

マイナスの概念も鬼の文字式計算も一般的に言いますと役に立たないものではございませんが、中学受験では役に立ちません。

なので上限はF教材まで。

つまり、F教材修了までがやめどき。

じゃあ下限はどこなの？

っていうと、D教材修了くらい、せっかくですからE教材修了までじゃないですかね。

なぜならD教材は分数の概念、E教材は分数の四則計算まで学習するからです。

分数は受験で苦労する子は苦労しますからね。

「え？うち小学4年生でC教材やってるけどD教材とかE教材まで頑張らなきゃいけないの？」

なんて声も聞こえてきそうです。

どうしても中学受験させたければ別にC教材までであっても、中学受験塾に乗り換えても構わないと思いますよ。

どうせ、DやE教材でやるような筆算も分数も中学受験塾でやりますからね。さらっと。

ですから公文式の到達点に拘泥する必要もないわけです。

ただし、中学受験に役立つから、という世間のささやきに駆られて公文に入ったとしても、C教材まででしたら直接的に役立つかどうかは疑問でございます。

あんまり意味ないんじゃねぇ？ってのが私の考えです。

せっかくですからD教材、E教材まで進みたいものです。

では中学受験を考えたときにいつから公文を始めたらE教材修了レベルまで到達できるのか。

始めどきも肝心です。

仮に、小学2年生から慌てて公文に入って中学受験バッチコイ！なんて鼻息荒くしても最初はA教材あたりからエッチラオッチラやっていくわけですよ。

小学2年生から小学3年生の2月までの約2年間でD教材もしくはE教材を修了するにはブーストかます必要がございます。

始めどき、そんなところからお話ししていきましょう。

中学受験を考えたときにいつから公文を始めるか

我ながらすごい命題を立ててしまいましてチビってしまいそうです。

むしろ漏らしているかもしれません。

さて、一般的に中学受験の学習が本格化するのは小学3年生の2月です。

では小学1年生から公文を始めて小学3年生の2月にE教材まで修了させるとしましょう。

小学1年生から公文に入ったとして大抵は3A、2Aくらいからのスタートです。

そこからE教材を駆逐することを考えますと、

3A→2A→A→B→C→D→E

7段階をクリアしないとE教材修了までたどり着きません。

楽勝じゃん！と思われる方はきっと天才キッズクラブの感覚の持ち主です。あるいはヨコミネ式か。いずれにせよ素晴らしいですね。

しかしながら、

「7段階を3年でクリアする」

これ、普通の子だったらかなり頑張って到達できるかどうかです。

3A、2A、Aくらいのレベルだったら割とトントントンと進むんですよ。

でもA教材の引き算でつまづいたり、B教材の3けたの計算あたりで牛歩戦術、C、D教材までいきますと1年がかりで1段階というのがザラです。

したがいまして、数の感覚に優れた子でないのなら年長さん、もしくは年中さんで公文式に帰依するのが中学受験を見据えた時の現実ラインでございます。

公文のやめどきにも困っているぞ

小学3年生でI教材とかJ教材！？

それはすごい。

何しろ代数分野で中学3年生までの学習をしてますからね。もう、マジで拍手です。すり切れるくらい。

ただ、これが中学受験に役立つかというと大して役に立ちません。

2次方程式の解の公式なんぞ問われませんし、連立方程式はむしろ学ばない方がいい。

ところが、時々小学2年生くらいでI教材だのJ教材だのをクリアしちゃう子がおります。

それはそれで素晴らしいんですけど、公文をあくまで中学受験塾のための予備校と捉えたときにはF教材までで十分。

F教材を修了していたとしたら公文の国語だけに専念するとか、あるいはピグマキッズくらぶにでも行っといた方がよっぽどいいです。

F教材以上をやっていてもあまり役に立ちませんし、何しろ公文の算数で身につけられるのは中学受験の算数のごく一部の能力ですから。

公文の算数で身につけられる能力

公文の算数で何が身につけられるのって、そりゃ計算力でしょ。

なんてのはみなさんご存知ですよね。

では中学受験で求められる算数の能力は何？公文の計算力はどこで役立つの？ってのが気になるところであります。

そこで中学受験の算数でどんな能力が求められるのか例によってヨレヨレのフリーハンドでしばいた図を描きますよ。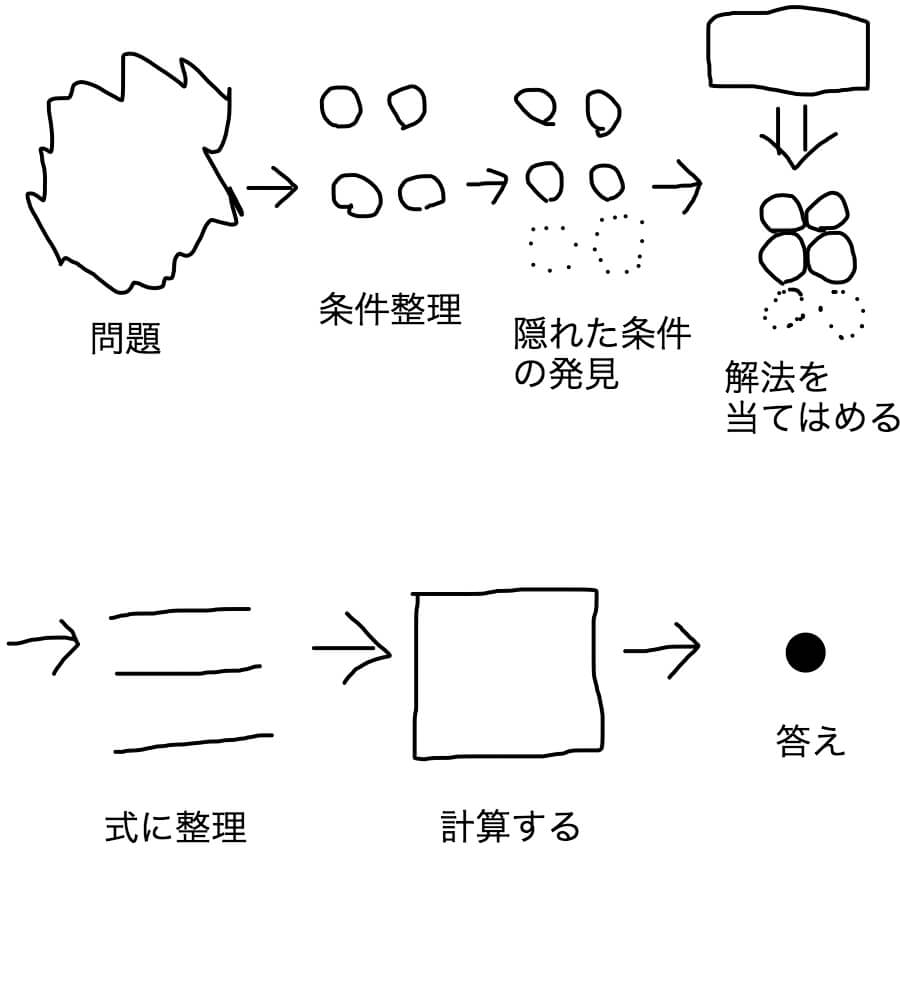

1.まずは問題の中から条件を拾い上げて整理し

2.その条件から分かること（隠れた条件）を見つけ出し

3.解法を当てはめ

4.式に整理し

5.計算し

答えを出す

これが中学受験の算数でやっていることです。

「うちの子、こんなに整理して解いてない・・・ッ！」

と崩れ落ちなくても結構です。

無意識のうちに頭の中でこんな作業をやってますから、必ずしもこの通りでなくても構いません。

ただ、こういった作業が必要なのは間違いございません。

次に上であげた算数の問題を解く手順のうち、どこで公文式が火を吹くのか見ていきましょう。

最前でも申し上げましたように、公文の算数で身につく能力は9割が計算力です。

上であげた変な図のうち公文で身につけた能力はどこで輝きそうですかね？

はい、5の「計算する」ですね。

つまり、中学受験の算数を解くために必要な能力を5つと定義しましたら、そのうちの1つだけ。

これが公文のアドバンテージです。

公文に月7,700円（税込）、年間92,400円（税込）払ってきた紳士淑女の皆様、がっかりすることはございません。

計算ができるってのは100%損になりませんからね。確実に計算力はつきます。

プレステ2台買ってお釣りがくるとしても我が子の成長・・・以下略。

ただ、公文やってたからって算数が得意になるとは限りません。

せいぜい算数における計算力だけの話です。

公文のメリットは計算力。

では逆にデメリットはあるんでしょうか？

ありません。

公文をやらせていたとしてもデメリットというデメリットはございません。

その代わり、公文で学んだ子どもにはある悪癖が身についてしまっているかもしれません。

一体何か。

世界不思議発見。

1 2 3 次へ >

あわせて読みたい

最新のホカホカ記事

書いている人の紹介